2.6.2 应用一元二次方程 课件(共28张PPT)
文档属性
| 名称 | 2.6.2 应用一元二次方程 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 10:01:06 | ||
图片预览






文档简介
2.6 应用一元二次方程(二)
2020年秋北师大版九年级上册
第二章
一元二次方程
一、知识回顾
关于利润的基本知识
(1)成本价(进货价)
(2)标价(定价)
(3)售价(成交价)
(4)利润=售价-进价
(5) 利润率 = ×100% =
利润
成本价
售价-成本价
成本价
(1)某公司今年的销售收入是a万元,如果每年的增长率都是x ,那么一年后的销售收入将达到 万元(用代数式表示).
(2)某公司今年的销售收入是a万元,如果每年的增长率都是x ,那么两年后的销售收入将达到 万元(用代数式表示).
a(1 + x)
a(1 + x)2
一、知识回顾
例1 :新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
二、探究新知
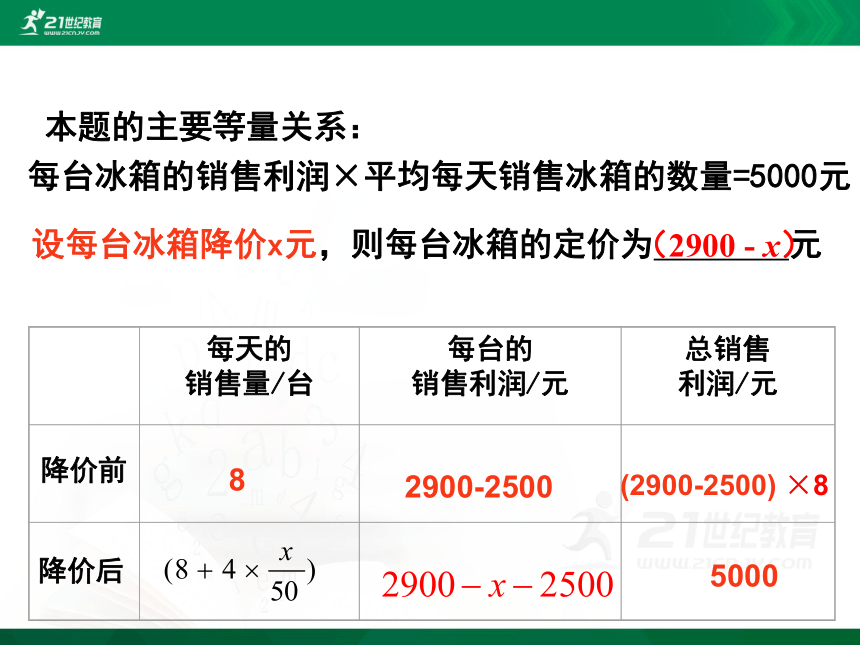
设每台冰箱降价x元,则每台冰箱的定价为 元
本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
8
2900-2500
(2900-2500) ×8
5000
(2900 - x)
解:设每台冰箱降价x元,根据题意,得
整理,得:x2 - 300x + 22500 = 0.
解方程,得:
x1 = x2 = 150.
∴ 2900 - x = 2900 - 150 = 2750.
答:每台冰箱的定价应为2750元.
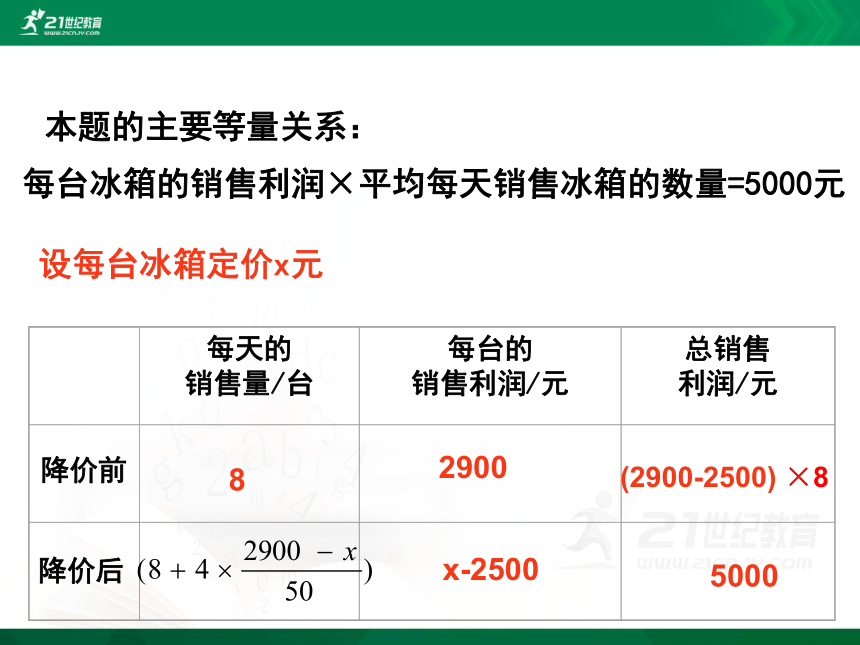
设每台冰箱定价x元
本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
8
2900
(2900-2500) ×8
5000
x-2500
解:设每台冰箱定价x元,根据题意,得
整理得:x2-5500x+7562500=0
解这个方程,得x1=x2=2750
答:每台冰箱的定价应为2750元。
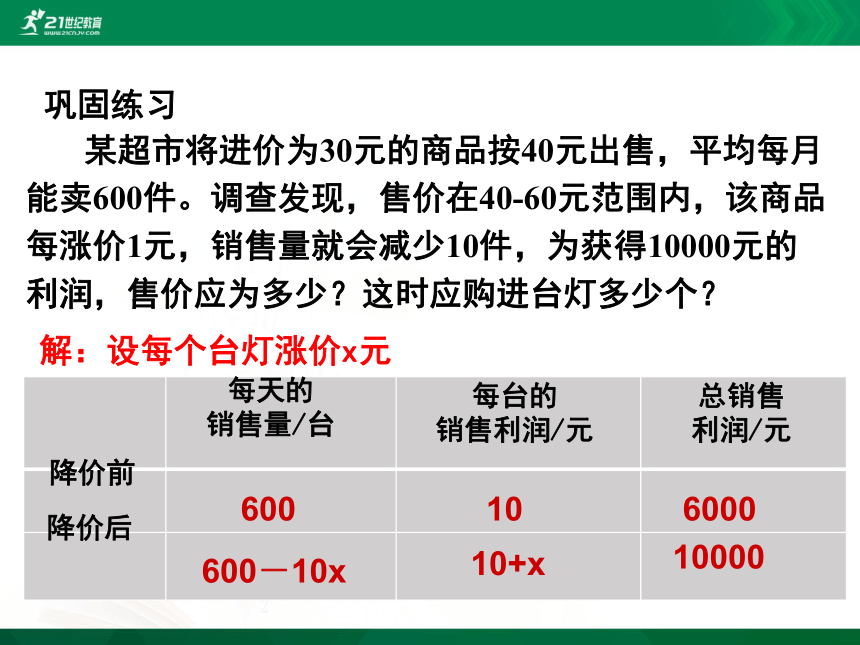
某超市将进价为30元的商品按40元出售,平均每月能卖600件。调查发现,售价在40-60元范围内,该商品每涨价1元,销售量就会减少10件,为获得10000元的利润,售价应为多少?这时应购进台灯多少个?
巩固练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
600
600-10x
10
10+x
6000
10000
解:设每个台灯涨价x元
解:设每个台灯涨价x元
根据题意,得(600-10x)(10+x)=10000
整理得:x2-50x+400=0
解这个方程,得x1=10,x2=40(不合题意,舍去)
40+10=50,600 -10×10=500.
答:每个台灯的售价应为50元,需购进台灯500个。
本题的主要等量关系:
每个台灯的销售利润×平均每月销售台灯的数量=10000元
基本关系:(1)利润=售价-________=进价×利润率;
(3)总利润=____________×销量
进价
单个利润
利润问题常见关系式
1.前年生产1吨甲种药品的成本是5000元,随着生产技
术的进步,去年生产1吨甲种药品的成本是4650 元。
(1)则下降率是 .
(2)保持这个下降率,那么今年生产1吨甲种药品的成本是 元.
7%
4324.5
下降率=
下降前的量-下降后的量
下降前的量
平均变化率问题与一元二次方程
下降后的量=下降前的量×(1-下降率)
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,设下降率是x,则去年生产1吨甲种药品的成本是 元,如果保持这个下降率,则现在生产1吨甲种药品的成本是 元.
下降率x
第一次降低前的量
5000(1-x)
第一次降低后的量
5000
下降率x
第二次降低后的量
第二次降低前的量
5000(1-x)(1-x)
5000(1-x)2
5000(1-x)
5000(1-x)2
平均变化率问题与一元二次方程
(1)增长率问题
增长率不可为负,但可以超过1.
设基数为a,平均增长率为x,
则一次增长后的值为:
二次增长后的值为:
依次类推n次增长后的值为:
a (1+x)
a (1+x)2
a (1+x)n
(2)降低率问题
设基数为a,平均增长率为x,
则一次增长后的值为:
二次增长后的值为:
依次类推n次增长后的值为:
a (1-x)
a (1-x)2
a (1-x)n
下降率不能超过1.
1.某商场一月份的利润为25万元,第三个月的利润为36万元,设利润月平均增长率为x,那么x满足的方程是 .
25(1+x)2=36
2.商品原价289元,经连续两次降价后售价为256元,设平均每次降价的百分率为x,那么x满足的方程是 .
289(1-x)2=256
三、典例讲解
3.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x。
那么x满足的方程是 .
50[1+(1+x)+(1+x)2]=196
4.某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x) +200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
增长率不可为负,但可以超过1.
5.某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的64%,那么这两年平均每年近视学生人数降低的百分率是多少?
提示:增长率问题中若基数不明确,通常可设为“1”,或设为a等,设为“1”更常用.
解:设平均每年近视学生人数降低的百分率为x, 前年近视人数为“1”,去年近视人数为(1 - x),今年近视人数为(1 - x)2.
(1 – x )2 = 0.64 .
解得, x1 = 0.2 , x2 = 1.8(不合题意,舍去).
答:平均每年近视学生人数降低的百分率为20%.
四、课堂练习
1.华润万家超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件. 为了迎接六一,商场决定采取适当的降价措施,扩大销售量,增加赢利. 经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装赢利1 200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )
A. (40-x )( 20+2x) =1 200
B. (40-x )( 20+x) =1 200
C. (50-x )( 20+2x) =1 200
D. (90-x )( 20+2x) =1 200
A
四、课堂练习
2.某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次,设参观人次的平均年增长率为x,则( )
A.10.8(1+x)=16.8 B.16.8(1-x)=10.8
C.10.8(1+x)2=16.8
D.10.8[(1+x)+(1+x)2]=16.8
C
3.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同. 设2,3月份利润的月增长率为x,那么x满足的方程为( )
A. 10(1+x)2=36.4
B. 10+10(1+x)2=36.4
C. 10+10(1+x)+10(1+2x)=36.4
D. 10+10(1+x)+10(1+x)2=36.4
D
四、课堂练习
4.某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6 080元的利润,则应将销售单价定为多少元?
解:设降价x元,则售价为(60-x)元,销售量为(300+20x)件
根据题意,得(60-x-40)(300+20x)=6 080.
解得x1=1,x2=4.
又要顾客得实惠,故取x=4,即定价为56元.
答:应将销售单价定为56元.
5.某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价0.05元,那么平均每天可多售出200张.摊主要想平均每天盈利180元,每张贺年卡应降价多少元?
解:设每张贺年卡降价x元,根据题意,得:
整理得:400x2-70x+3=0
解方程,得 x1=0.1, x2=0.075(最小单位是分,舍去)
所以,每张贺年卡应降价0.1元。
6.某地2018年为做好“精准扶贫”,投入资金1 280万元用于异地安置,并规划投入资金逐年增加,2020年在2018年的基础上增加投入资金1 600万元.求从2018年到2020年,该地投入异地安置资金的年平均增长率为多少?
四、课堂练习
解:设该地投入异地安置资金的年平均增长率为x,得
1 280(1+x)2=1 280+1 600.
解得x1=0.5或x2=-2.5(舍去).
答:从2018年到2020年,该地投入异地安置资金的年平均增长率为50%.
7.某商场今年1月份的销售额为60万元,2月份的销售额下降10%,改进经营管理后月销售额大幅度上升,到4月份销售额已达到121.5万元,求3,4月份销售额的月平均增长率.
解:设3,4月份销售额的月平均增长率为x,得
60(1 - 10%)(1+x) = 121.5 则 (1+ x)2=2.25.
解得, x1 = 0.5 , x2 = - 2.5(不合题意,舍去).
答:3,4月份销售额的月平均增长率为50%.
四、课堂练习
8.某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1间客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/天的维护费用,设每间客房的定价提高了x元.若该青年旅社希望每天纯收入为14 000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入-维护费用)
四、课堂练习
解:依题意,得
整理,得x2-420x+32 000=0.
解得x1=320,x2=100.
当x=320时,游客居住的客房数是:60-0.1x=28(间)
四、课堂练习
当x=100时,游客居住的客房数是:60-0,1x=50(间).
所以当x=100时,能吸引更多的游客,
则每个房间的定价为200+100=300(元).
答:每间客房的定价应为300元.
五、课堂小结
关键:寻找等量关系
利用一元二次方程解决营销问题及平均变化率问题
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
基本关系:(1)利润=售价-________=进价×利润率;
(3)总利润=____________×销量
进价
单个利润
六、布置作业
课本P55 习题2.10 第1,2,3,4题
2020年秋北师大版九年级上册
第二章
一元二次方程
一、知识回顾
关于利润的基本知识
(1)成本价(进货价)
(2)标价(定价)
(3)售价(成交价)
(4)利润=售价-进价
(5) 利润率 = ×100% =
利润
成本价
售价-成本价
成本价
(1)某公司今年的销售收入是a万元,如果每年的增长率都是x ,那么一年后的销售收入将达到 万元(用代数式表示).
(2)某公司今年的销售收入是a万元,如果每年的增长率都是x ,那么两年后的销售收入将达到 万元(用代数式表示).
a(1 + x)
a(1 + x)2
一、知识回顾
例1 :新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
二、探究新知
设每台冰箱降价x元,则每台冰箱的定价为 元
本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
8
2900-2500
(2900-2500) ×8
5000
(2900 - x)
解:设每台冰箱降价x元,根据题意,得
整理,得:x2 - 300x + 22500 = 0.
解方程,得:
x1 = x2 = 150.
∴ 2900 - x = 2900 - 150 = 2750.
答:每台冰箱的定价应为2750元.
设每台冰箱定价x元
本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
8
2900
(2900-2500) ×8
5000
x-2500
解:设每台冰箱定价x元,根据题意,得
整理得:x2-5500x+7562500=0
解这个方程,得x1=x2=2750
答:每台冰箱的定价应为2750元。
某超市将进价为30元的商品按40元出售,平均每月能卖600件。调查发现,售价在40-60元范围内,该商品每涨价1元,销售量就会减少10件,为获得10000元的利润,售价应为多少?这时应购进台灯多少个?
巩固练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?
每天的
销售量/台
每台的
销售利润/元
总销售
利润/元
降价前
?
?
?
降价后
?
?
?
600
600-10x
10
10+x
6000
10000
解:设每个台灯涨价x元
解:设每个台灯涨价x元
根据题意,得(600-10x)(10+x)=10000
整理得:x2-50x+400=0
解这个方程,得x1=10,x2=40(不合题意,舍去)
40+10=50,600 -10×10=500.
答:每个台灯的售价应为50元,需购进台灯500个。
本题的主要等量关系:
每个台灯的销售利润×平均每月销售台灯的数量=10000元
基本关系:(1)利润=售价-________=进价×利润率;
(3)总利润=____________×销量
进价
单个利润
利润问题常见关系式
1.前年生产1吨甲种药品的成本是5000元,随着生产技
术的进步,去年生产1吨甲种药品的成本是4650 元。
(1)则下降率是 .
(2)保持这个下降率,那么今年生产1吨甲种药品的成本是 元.
7%
4324.5
下降率=
下降前的量-下降后的量
下降前的量
平均变化率问题与一元二次方程
下降后的量=下降前的量×(1-下降率)
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,设下降率是x,则去年生产1吨甲种药品的成本是 元,如果保持这个下降率,则现在生产1吨甲种药品的成本是 元.
下降率x
第一次降低前的量
5000(1-x)
第一次降低后的量
5000
下降率x
第二次降低后的量
第二次降低前的量
5000(1-x)(1-x)
5000(1-x)2
5000(1-x)
5000(1-x)2
平均变化率问题与一元二次方程
(1)增长率问题
增长率不可为负,但可以超过1.
设基数为a,平均增长率为x,
则一次增长后的值为:
二次增长后的值为:
依次类推n次增长后的值为:
a (1+x)
a (1+x)2
a (1+x)n
(2)降低率问题
设基数为a,平均增长率为x,
则一次增长后的值为:
二次增长后的值为:
依次类推n次增长后的值为:
a (1-x)
a (1-x)2
a (1-x)n
下降率不能超过1.
1.某商场一月份的利润为25万元,第三个月的利润为36万元,设利润月平均增长率为x,那么x满足的方程是 .
25(1+x)2=36
2.商品原价289元,经连续两次降价后售价为256元,设平均每次降价的百分率为x,那么x满足的方程是 .
289(1-x)2=256
三、典例讲解
3.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x。
那么x满足的方程是 .
50[1+(1+x)+(1+x)2]=196
4.某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x) +200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
增长率不可为负,但可以超过1.
5.某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的64%,那么这两年平均每年近视学生人数降低的百分率是多少?
提示:增长率问题中若基数不明确,通常可设为“1”,或设为a等,设为“1”更常用.
解:设平均每年近视学生人数降低的百分率为x, 前年近视人数为“1”,去年近视人数为(1 - x),今年近视人数为(1 - x)2.
(1 – x )2 = 0.64 .
解得, x1 = 0.2 , x2 = 1.8(不合题意,舍去).
答:平均每年近视学生人数降低的百分率为20%.
四、课堂练习
1.华润万家超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件. 为了迎接六一,商场决定采取适当的降价措施,扩大销售量,增加赢利. 经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装赢利1 200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )
A. (40-x )( 20+2x) =1 200
B. (40-x )( 20+x) =1 200
C. (50-x )( 20+2x) =1 200
D. (90-x )( 20+2x) =1 200
A
四、课堂练习
2.某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次,设参观人次的平均年增长率为x,则( )
A.10.8(1+x)=16.8 B.16.8(1-x)=10.8
C.10.8(1+x)2=16.8
D.10.8[(1+x)+(1+x)2]=16.8
C
3.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同. 设2,3月份利润的月增长率为x,那么x满足的方程为( )
A. 10(1+x)2=36.4
B. 10+10(1+x)2=36.4
C. 10+10(1+x)+10(1+2x)=36.4
D. 10+10(1+x)+10(1+x)2=36.4
D
四、课堂练习
4.某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6 080元的利润,则应将销售单价定为多少元?
解:设降价x元,则售价为(60-x)元,销售量为(300+20x)件
根据题意,得(60-x-40)(300+20x)=6 080.
解得x1=1,x2=4.
又要顾客得实惠,故取x=4,即定价为56元.
答:应将销售单价定为56元.
5.某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价0.05元,那么平均每天可多售出200张.摊主要想平均每天盈利180元,每张贺年卡应降价多少元?
解:设每张贺年卡降价x元,根据题意,得:
整理得:400x2-70x+3=0
解方程,得 x1=0.1, x2=0.075(最小单位是分,舍去)
所以,每张贺年卡应降价0.1元。
6.某地2018年为做好“精准扶贫”,投入资金1 280万元用于异地安置,并规划投入资金逐年增加,2020年在2018年的基础上增加投入资金1 600万元.求从2018年到2020年,该地投入异地安置资金的年平均增长率为多少?
四、课堂练习
解:设该地投入异地安置资金的年平均增长率为x,得
1 280(1+x)2=1 280+1 600.
解得x1=0.5或x2=-2.5(舍去).
答:从2018年到2020年,该地投入异地安置资金的年平均增长率为50%.
7.某商场今年1月份的销售额为60万元,2月份的销售额下降10%,改进经营管理后月销售额大幅度上升,到4月份销售额已达到121.5万元,求3,4月份销售额的月平均增长率.
解:设3,4月份销售额的月平均增长率为x,得
60(1 - 10%)(1+x) = 121.5 则 (1+ x)2=2.25.
解得, x1 = 0.5 , x2 = - 2.5(不合题意,舍去).
答:3,4月份销售额的月平均增长率为50%.
四、课堂练习
8.某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1间客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/天的维护费用,设每间客房的定价提高了x元.若该青年旅社希望每天纯收入为14 000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入-维护费用)
四、课堂练习
解:依题意,得
整理,得x2-420x+32 000=0.
解得x1=320,x2=100.
当x=320时,游客居住的客房数是:60-0.1x=28(间)
四、课堂练习
当x=100时,游客居住的客房数是:60-0,1x=50(间).
所以当x=100时,能吸引更多的游客,
则每个房间的定价为200+100=300(元).
答:每间客房的定价应为300元.
五、课堂小结
关键:寻找等量关系
利用一元二次方程解决营销问题及平均变化率问题
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
基本关系:(1)利润=售价-________=进价×利润率;
(3)总利润=____________×销量
进价
单个利润
六、布置作业
课本P55 习题2.10 第1,2,3,4题
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
