1.3 位置变化快慢的描述 速度—【新教材】人教版(2019)高中物理必修第一册课件(共34张PPT)
文档属性
| 名称 | 1.3 位置变化快慢的描述 速度—【新教材】人教版(2019)高中物理必修第一册课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 17.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-10 08:05:09 | ||
图片预览






文档简介
(共34张PPT)
第三节 位置变化快慢的描述——速度
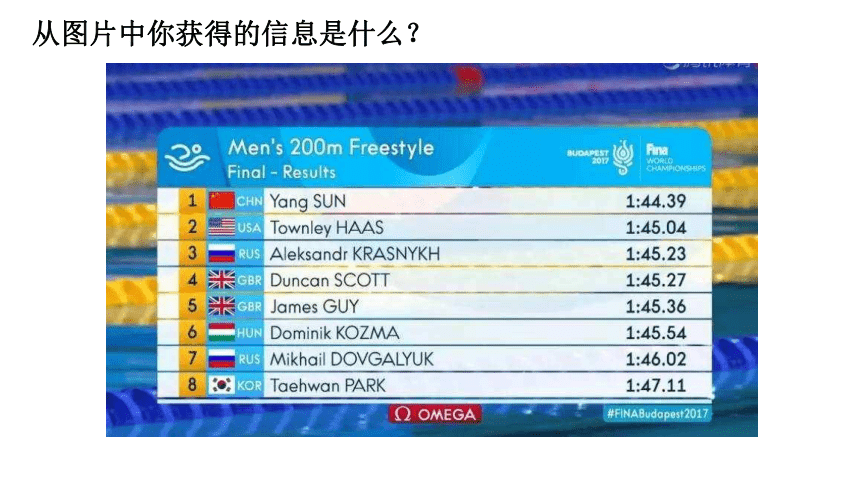
你获得的信息是什么?
从图片中你获得的信息是什么?
初中速度的回忆
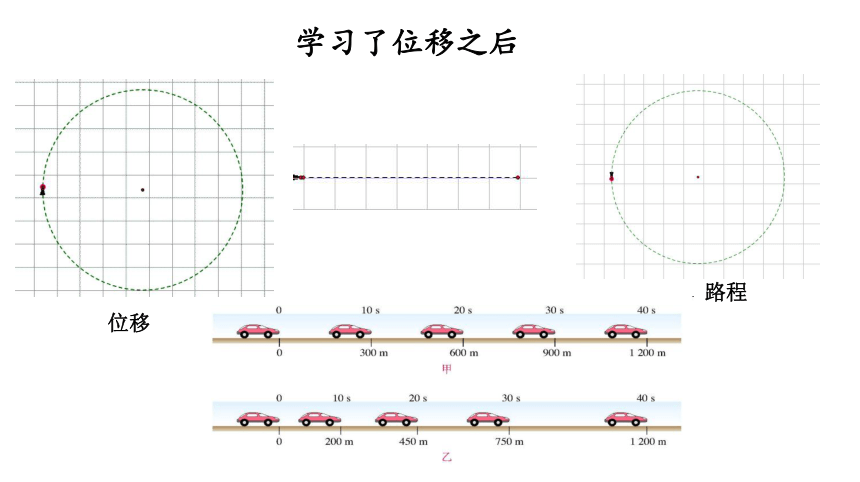
学习了位移之后
位移
路程
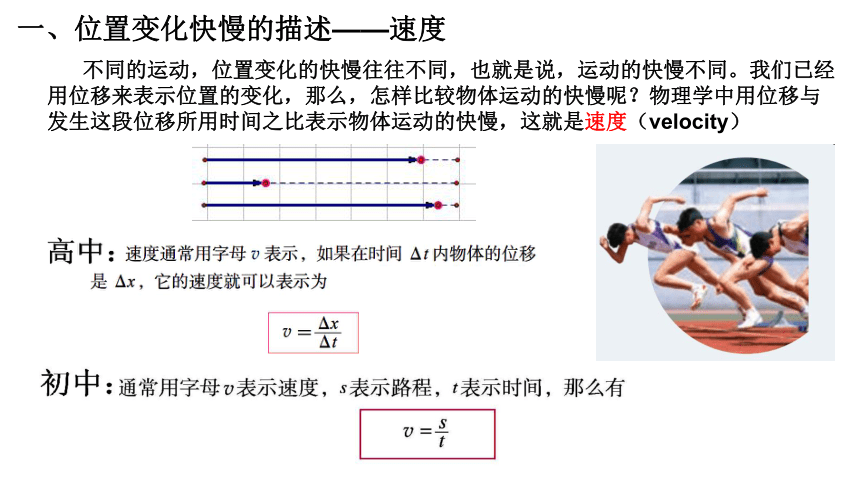
一、位置变化快慢的描述——速度
不同的运动,位置变化的快慢往往不同,也就是说,运动的快慢不同。我们已经用位移来表示位置的变化,那么,怎样比较物体运动的快慢呢?物理学中用位移与发生这段位移所用时间之比表示物体运动的快慢,这就是速度(velocity)
Δx与Δt具有对应性
1、速度公式:
(2)如果t时间内物体发生的位移为x,公式可表示成
Δx为Δt
内物体的位移
Δt为通过Δx对应的时间
(1)
(3)在国际单位制中,速度的单位是米每秒,符号是
m/s
或
m·s-1。
常用的单位还有千米每时(km/h
或
km·h-1
)、厘
米每秒(cm/s
或
cm·s-1
)等。
单位换算关系:1
m/s=
3.6km/h
(4)速度的物理意义:
①速度是描述物体位置变化快慢的物理量,v也叫物体位置的变化率,速度越大,表示物体运动得越快,其位置变化得也就越快。
②速度是表示物体运动快慢和方向的物理量
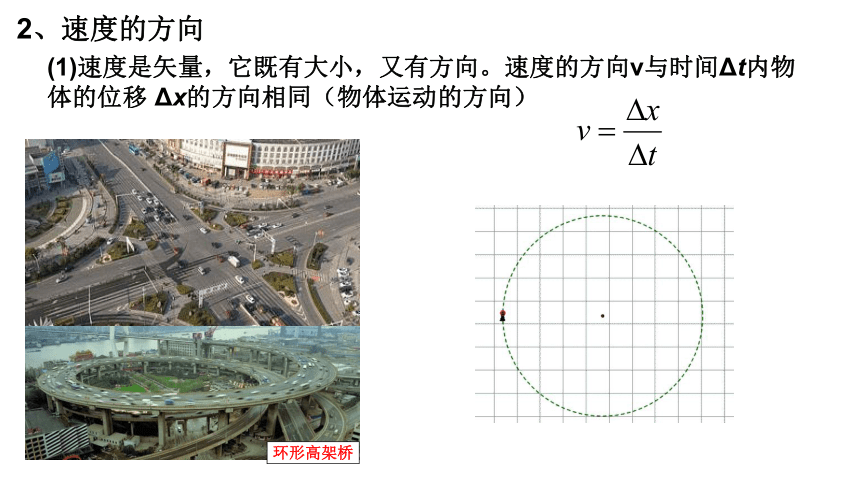
2、速度的方向
(1)速度是矢量,它既有大小,又有方向。速度的方向v与时间Δt内物体的位移
Δx的方向相同(物体运动的方向)
环形高架桥
2.速度方向的表示方法:
物体做直线运动时,可沿运动方向建立直线坐标系,物体的速度就可用正、负号表示,速度的方向与规定的正方向相同时取正值,相反时取负值。
3、比较两个速度是否相同时,既要比较其大小是否相等,又要比较其方向是否相同.
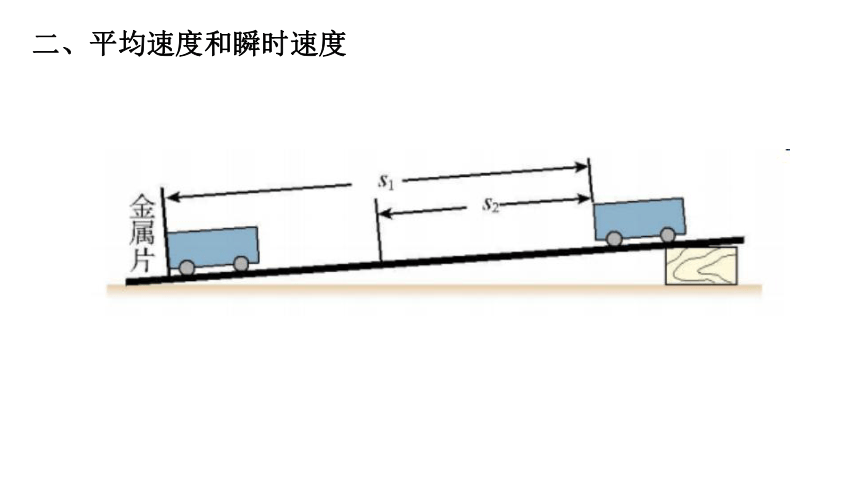
二、平均速度和瞬时速度
(一)平均速度
2、物理意义:描述物体在一段时间内运动的平均快慢程度和方向.由于是一段时间的平均值所以是粗略地描述物体在时间间隔△t内的平均快慢程度。
3、定义式:
4、平均速度的方向:与时间Δt内物体的位移
Δx的方向相同,如果物体的的起点为零则物体的速度方向与物体的位移x的方向相同。
常见的两种情况
(二)瞬时速度
2、物理意义:描述物体在某一时刻运动的快慢。可以准确的描述物体运动的快慢
3、匀速直线运动:瞬时速度保持不变的运动。在匀速直线运动中,平均速度与瞬时速度相等。
4、瞬时速度的大小通常叫作速率(speed)。汽车速度计
不能显示车辆运动的方向,它的示数实际是汽车的速率
(图
1.3-1)。日常生活中说到的“速度”,有时是指速率,
图
1.3-1
汽车速度计
要根据上下文判断。
(三)平均速度和瞬时速度的比较
(四)平均速度和平均速率的比较
(五)测量纸带的平均速度和瞬时速度
1、测量平均速度
每隔
0.1
s
(或更短)计算一次平均速度。
1.
在图
1.3-2
中选取纸带上一点为起始点
0,后面每
5
个点取一个计数点,分别用数
字
1,2,3,…
标出这些计数点;
2.
测量各计数点到起始点
0
的距离
x,记录在表
1
中;
3.
计算两相邻计数点间的位移
Δx,同时记录对应的时间
Δt;
4.
根据
Δx
和
Δt
计算纸带在相邻计数点间的平均速度
v。
2、测量瞬时速度
下面考虑如何测量图
1.3-2
中
E
点的瞬
时速度。
E
点在
D、G
两点之间,
D、G
两点间的平均速度我
们可以求出。如果不要求很精确,用这个平均速度粗略地
代表
E
点的瞬时速度,也未尝不可。不过,如果把包含
E
点在内的间隔取得小一些,例如取图
1.3-3
中的
DF
线段,
那么经过
D、F
两点所用的时间
Δt
就会变短,用两点间的
位移
Δx
和时间
Δt
算出的平均速度代表纸带在
E
点的瞬
时速度,就会精确一些。D、F
两点离
E
点越近,算出的平
均速度越接近
E
点的瞬时速度。
请根据上述测量瞬时速度的方法,计算上节实验中纸带上各计数点的瞬时速度。
每隔
0.06
s
计算一次速度。
1.
从纸带起始点
0
算起,后面每
3
个点取一个计数点;
2.
测量各计数点到起始点
0
的距离
x,记录在表
2
中;
3.
计算两相邻计数点间的位移
Δx,同时记录对应的时间
Δt;
4.
根据
Δx
和
Δt
算出的速度值就可以代表在
Δx
这一区间内任意一点的瞬时速度。
将算出的各计数点的速度值记录在表
2
中。
三、速度—时间图像
物体运动的速度随时间变化的情况可以用图像来直观
表示。以时间
t
为横轴,速度
v
为纵轴,坐标中的图像即
为速度—时间图像或
v-t
图像。v
?
t图像非常直观地反映了物体运动的速度随时间变化的规律,它并不表示物体运动的轨迹.
1、匀速直线运动的速度-时间图像
如图所示的图像中速度的正负表示什么?
2、变速直线运动
(1)
v
?
t图像的建立
①用横轴表示时间t,纵轴表示速度v,建立直角坐标系.
②根据测量的速度v、时间t数据在坐标系中描点.
③用平滑的曲线把这些点连接起来,即得到如图所示的v
?
t图像.
(2)图
甲是根据某同学的实测数据所描的点,从这
些点的走向能够大致看出纸带运动速度的变化规律。为了
更清晰些,可以用折线把这些点连起来(图
乙)。然
而我们知道,通常速度不会发生突变,所以,如果用一条
平滑的曲线来描出这些点,曲线所反映的情况就会与实际
更加接近(图丙)。
3、一种特殊的变速直线运动(速度随时间均匀变化)
四、借助传感器与计算机测速度
课堂练习
CD
B
BCD
C
第三节 位置变化快慢的描述——速度
你获得的信息是什么?
从图片中你获得的信息是什么?
初中速度的回忆
学习了位移之后
位移
路程
一、位置变化快慢的描述——速度
不同的运动,位置变化的快慢往往不同,也就是说,运动的快慢不同。我们已经用位移来表示位置的变化,那么,怎样比较物体运动的快慢呢?物理学中用位移与发生这段位移所用时间之比表示物体运动的快慢,这就是速度(velocity)
Δx与Δt具有对应性
1、速度公式:
(2)如果t时间内物体发生的位移为x,公式可表示成
Δx为Δt
内物体的位移
Δt为通过Δx对应的时间
(1)
(3)在国际单位制中,速度的单位是米每秒,符号是
m/s
或
m·s-1。
常用的单位还有千米每时(km/h
或
km·h-1
)、厘
米每秒(cm/s
或
cm·s-1
)等。
单位换算关系:1
m/s=
3.6km/h
(4)速度的物理意义:
①速度是描述物体位置变化快慢的物理量,v也叫物体位置的变化率,速度越大,表示物体运动得越快,其位置变化得也就越快。
②速度是表示物体运动快慢和方向的物理量
2、速度的方向
(1)速度是矢量,它既有大小,又有方向。速度的方向v与时间Δt内物体的位移
Δx的方向相同(物体运动的方向)
环形高架桥
2.速度方向的表示方法:
物体做直线运动时,可沿运动方向建立直线坐标系,物体的速度就可用正、负号表示,速度的方向与规定的正方向相同时取正值,相反时取负值。
3、比较两个速度是否相同时,既要比较其大小是否相等,又要比较其方向是否相同.
二、平均速度和瞬时速度
(一)平均速度
2、物理意义:描述物体在一段时间内运动的平均快慢程度和方向.由于是一段时间的平均值所以是粗略地描述物体在时间间隔△t内的平均快慢程度。
3、定义式:
4、平均速度的方向:与时间Δt内物体的位移
Δx的方向相同,如果物体的的起点为零则物体的速度方向与物体的位移x的方向相同。
常见的两种情况
(二)瞬时速度
2、物理意义:描述物体在某一时刻运动的快慢。可以准确的描述物体运动的快慢
3、匀速直线运动:瞬时速度保持不变的运动。在匀速直线运动中,平均速度与瞬时速度相等。
4、瞬时速度的大小通常叫作速率(speed)。汽车速度计
不能显示车辆运动的方向,它的示数实际是汽车的速率
(图
1.3-1)。日常生活中说到的“速度”,有时是指速率,
图
1.3-1
汽车速度计
要根据上下文判断。
(三)平均速度和瞬时速度的比较
(四)平均速度和平均速率的比较
(五)测量纸带的平均速度和瞬时速度
1、测量平均速度
每隔
0.1
s
(或更短)计算一次平均速度。
1.
在图
1.3-2
中选取纸带上一点为起始点
0,后面每
5
个点取一个计数点,分别用数
字
1,2,3,…
标出这些计数点;
2.
测量各计数点到起始点
0
的距离
x,记录在表
1
中;
3.
计算两相邻计数点间的位移
Δx,同时记录对应的时间
Δt;
4.
根据
Δx
和
Δt
计算纸带在相邻计数点间的平均速度
v。
2、测量瞬时速度
下面考虑如何测量图
1.3-2
中
E
点的瞬
时速度。
E
点在
D、G
两点之间,
D、G
两点间的平均速度我
们可以求出。如果不要求很精确,用这个平均速度粗略地
代表
E
点的瞬时速度,也未尝不可。不过,如果把包含
E
点在内的间隔取得小一些,例如取图
1.3-3
中的
DF
线段,
那么经过
D、F
两点所用的时间
Δt
就会变短,用两点间的
位移
Δx
和时间
Δt
算出的平均速度代表纸带在
E
点的瞬
时速度,就会精确一些。D、F
两点离
E
点越近,算出的平
均速度越接近
E
点的瞬时速度。
请根据上述测量瞬时速度的方法,计算上节实验中纸带上各计数点的瞬时速度。
每隔
0.06
s
计算一次速度。
1.
从纸带起始点
0
算起,后面每
3
个点取一个计数点;
2.
测量各计数点到起始点
0
的距离
x,记录在表
2
中;
3.
计算两相邻计数点间的位移
Δx,同时记录对应的时间
Δt;
4.
根据
Δx
和
Δt
算出的速度值就可以代表在
Δx
这一区间内任意一点的瞬时速度。
将算出的各计数点的速度值记录在表
2
中。
三、速度—时间图像
物体运动的速度随时间变化的情况可以用图像来直观
表示。以时间
t
为横轴,速度
v
为纵轴,坐标中的图像即
为速度—时间图像或
v-t
图像。v
?
t图像非常直观地反映了物体运动的速度随时间变化的规律,它并不表示物体运动的轨迹.
1、匀速直线运动的速度-时间图像
如图所示的图像中速度的正负表示什么?
2、变速直线运动
(1)
v
?
t图像的建立
①用横轴表示时间t,纵轴表示速度v,建立直角坐标系.
②根据测量的速度v、时间t数据在坐标系中描点.
③用平滑的曲线把这些点连接起来,即得到如图所示的v
?
t图像.
(2)图
甲是根据某同学的实测数据所描的点,从这
些点的走向能够大致看出纸带运动速度的变化规律。为了
更清晰些,可以用折线把这些点连起来(图
乙)。然
而我们知道,通常速度不会发生突变,所以,如果用一条
平滑的曲线来描出这些点,曲线所反映的情况就会与实际
更加接近(图丙)。
3、一种特殊的变速直线运动(速度随时间均匀变化)
四、借助传感器与计算机测速度
课堂练习
CD
B
BCD
C
