人教版高中物理必修1第四章第3节牛顿第二定律经典例题(共28张PPT)
文档属性
| 名称 | 人教版高中物理必修1第四章第3节牛顿第二定律经典例题(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-10 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
牛顿第二定律的应用
一、
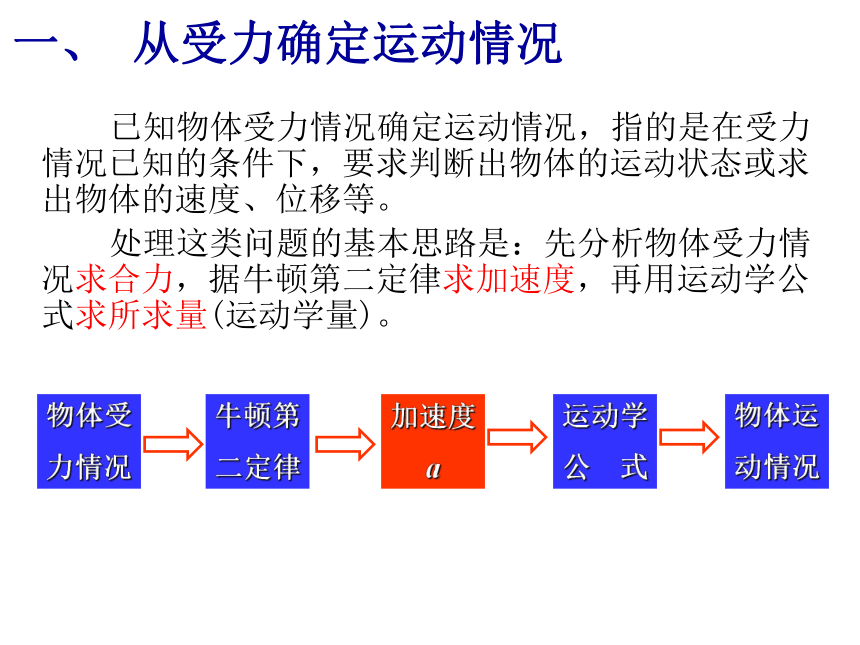
从受力确定运动情况
已知物体受力情况确定运动情况,指的是在受力情况已知的条件下,要求判断出物体的运动状态或求出物体的速度、位移等。
处理这类问题的基本思路是:先分析物体受力情况求合力,据牛顿第二定律求加速度,再用运动学公式求所求量(运动学量)。
物体运
动情况
运动学
公
式
加速度
a
牛顿第
二定律
物体受
力情况
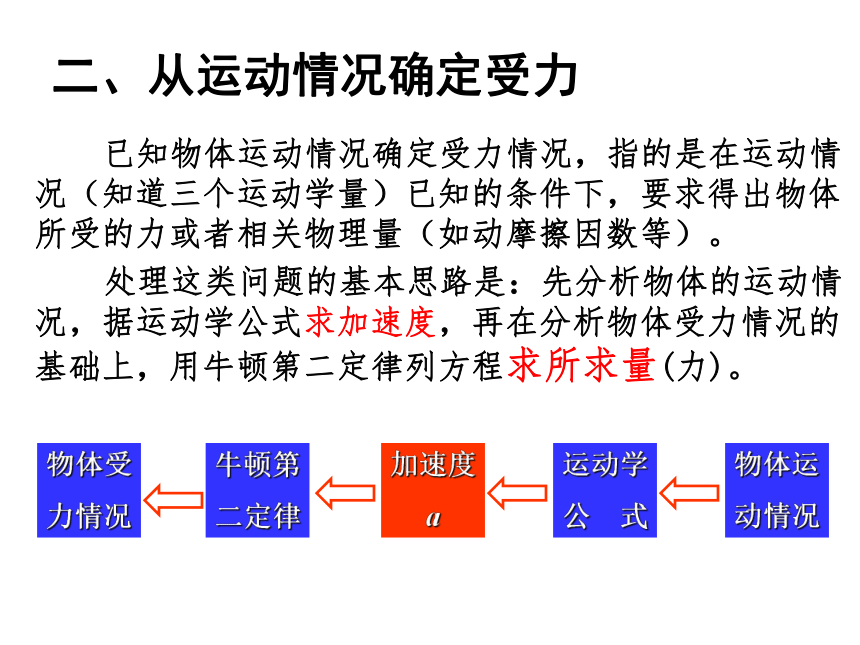
二、从运动情况确定受力
已知物体运动情况确定受力情况,指的是在运动情况(知道三个运动学量)已知的条件下,要求得出物体所受的力或者相关物理量(如动摩擦因数等)。
处理这类问题的基本思路是:先分析物体的运动情况,据运动学公式求加速度,再在分析物体受力情况的基础上,用牛顿第二定律列方程求所求量(力)。
物体运
动情况
运动学
公
式
加速度
a
牛顿第
二定律
物体受
力情况
解:木箱受力如图:将F正交分解,则:
一木箱质量为m=10Kg,与水平地面间的动摩擦因数为μ=0.2,现用斜向右下方F=100N的力推木箱,使木箱在水平面上做匀加速运动。F与水平方向成θ=37O角,求经过t=5秒时木箱的速度。
FN
mg
Ff
F
θ
F1
F2
F2=
F
sinθ
②
F1=
F
cosθ
①
Ff=μFN
⑤
由①②③④⑤
⑥得
竖直方向:
③
水平方向:
④
v
=at
⑥
代入数据可得:
v
=24m/s
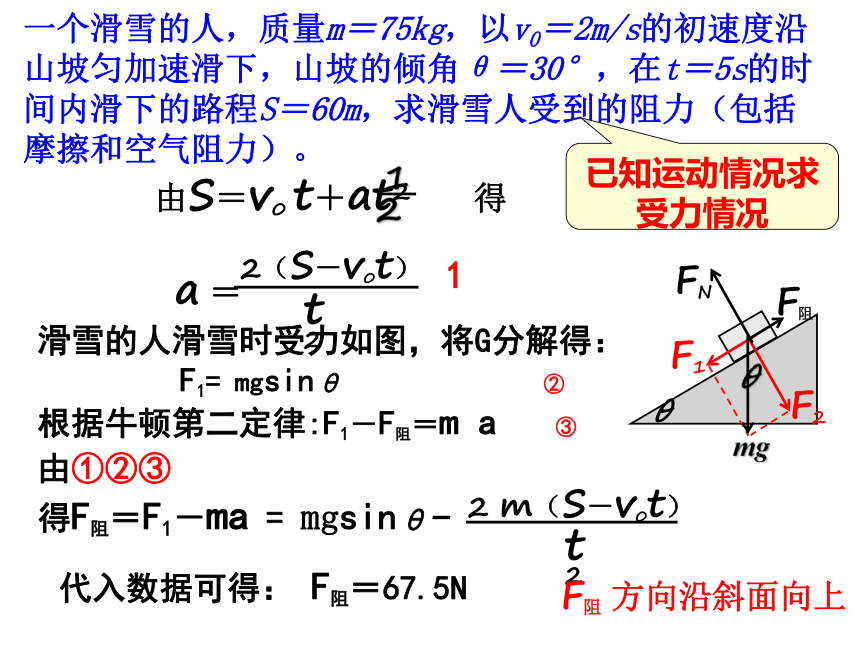
一个滑雪的人,质量m=75kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=30°,在t=5s的时间内滑下的路程S=60m,求滑雪人受到的阻力(包括摩擦和空气阻力)。
θ
F2
F1
θ
mg
F阻
FN
F1=
mgsinθ
②
根据牛顿第二定律:F1-F阻=m
a
③
1
2
由S=v0
t+at2
得
a
=
t2
2(S-v0t)
由①②③
得F阻=F1-ma
=
mgsinθ-
t2
2
m(S-v0t)
已知运动情况求受力情况
F阻
方向沿斜面向上
滑雪的人滑雪时受力如图,将G分解得:
代入数据可得:
F阻=67.5N
1
一木箱质量为m,与水平地面间的动摩擦因数为μ,现用斜向右下方与水平方向成θ角的力F推木箱,求从静止开始经过
t
秒时木箱的速度?
G
N
f
θ
Vt=?
V0=
0
F
Fcosθ
Fsinθ
竖直方向
N–
Fsinθ
=
G???①
水平方向
Fcosθ-
f
=
ma??
②
二者联系
f=μN?????????????
③
如果还要求经过
t
秒时木箱的速度vt=a
t
连结体问题:
连结体:两个(或两个以上)物体相互连 结参与运动的系统。
隔离法,整体法
光滑的水平面上有质量分别为m1、m2的两物体
静止靠在一起(如图)
,现对m1施加一个大小为
F
方向向右的推力作用。求此时物体m2受到物体
m1的作用力F1
m1
m2
F
[m1]
F
F1
[m2]
F1
FN1
[
解法一
]:
分别以m1、m2为隔离体作受力分析
FN2
m1g
m2g
对m1有
:F
–
F1
=
m
1a
(1)
对m2有:
F1
=
m2
a
(2)
联立(1)、(2)可得
F1
=
m1
m2
F
[m2]
F1
FN2
[
解法二
]:
对m1、m2视为整体作受力分析
m2g
有
:F
=
(m
1+
m2)a
(1)
对m2作受力分析
联立(1)、(2)可得
F1
=
FN
(m1
+
m2)g
F
有
:F1
=
m2
a
(2)
光滑的水平面上有质量分别为m1、m2的两物体
静止靠在一起(如图)
,现对m1施加一个大小为
F
方向向右的推力作用。求此时物体m2受到物体
m1的作用力F1
求m1对m2的作用力大小。
m1
m2
m2g
F1
FN
Ff
用水平推力F向左推
m1、m2间的作用力与原来相同吗?
对m2受力分析:
思考:
m
M
θ
F
例4.质量为M的斜面放置于水平面上,其上有质量为m
的小物块,各接触面均无摩擦力,将水平力
F加在M上,要求m与M不发生相对滑动,力F应为多大?
解:以m为对象;其受力如图:由图可得:
动
力
学
中
的
临
界
极
值
问
题
瞬时加速度的分析问题
分析物体在某一时刻的瞬时加速度,关键——分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
有两种模型:
①刚性绳(或接触面):是一种不需要发生明显形变就能产生弹力的物体,若剪断(或脱离)后,其中弹力立即发生变化,不需要形变恢复的时间。
②弹簧(或橡皮绳):特点是形变量大,形变恢复需要较长时间,在瞬时问题中,其弹力可以看成不变。
一条轻弹簧上端固定在天花板上,下端连接一物体A,A的下边通过一轻绳连接物体B。A、B的质量相同均为m,待平衡后剪断A、B间的细绳,则剪断细绳的瞬间,物体A、B加速度和方向?
A
B
A
B
如图,两个质量均为m的重物静止,若剪断绳OA,则剪断瞬间A和B的加速度分别是多少?
0
质量皆为m的A,B两球之间系着一个不计质量的轻弹簧,放在光滑水平台面上,A球紧靠墙壁,今用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间A,B的加速度分别为多少?
两物体P,Q分别固定在质量可以忽略不计的弹簧的两端,竖直放在一块水平板上并处于平衡状态,两物体的质量相等,如突然把平板撤开,在刚撤开的瞬间P,Q的加速度各是多少?
Q
P
如图,
质量为m的小球处于静止状态,若将绳剪断,则此瞬间小球的加速度是多少?
B
m
A
θ
如图所示,吊篮A、物体B、物体C的质量均为m,B和C分别固定在竖直弹簧两端,弹簧的质量不计.整个系统在轻绳悬挂下处于静止状态.现将悬挂吊篮的轻绳剪断,在轻绳刚断的瞬间( )
A.物体B的加速度大小为g
B.物体C的加速度大小为2g
C.吊篮A的加速度大小为3g
D.A、C间的弹力大小为0.5mg
D
可能一直加速
(2)可能先加速后匀速
⑴v0>v时,可能一直减速,也可能先减速再匀速
(2)v0<v时,可能一直加速,也可能先加速再匀速
传送带较短时,滑块一直减速达到左端
(2)传送带较长时,滑块还要被传送带传回右端.其中v0>v返回时速度为v,当v0<v返回时速度为v0
模型 传送带模型
可能一直加速
(2)可能先加速后匀速
⑴可能一直加速
(2)可能一直匀速
(3)可能先减速后反向加速
可能一直加速
(2)可能先加速后匀速
(3)可能先以a1加速后以a2加速
可能一直加速
(2)可能先加速后匀速
(3)可能一直匀速
(4)可能先以a1加速后以a2加速
模型 “等时圆”模型
图中的AB、AC、AD都是光滑的轨道,A、B、C、D四点在同一竖直圆周上,其中AD是竖直的。一小球从A点由静止开始,分别沿AB、AC、AD轨道滑下B、C、D点所用的时间分别为tl、t2、t3。则
A.tl=t2=t3
B.tl>t2>t3
C.tlD.t3>tl>t2
V0
θ
物体以某一初速度v0冲上倾角为θ的斜面,物体与斜面间的动摩擦因数为μ,则物体经多长时间上滑至最高点?
θ
小车的斜面光滑,倾角为θ,木块位于斜面上,则小车应以什么样的加速度运动才能使木块与它保持相对静止?
判断车在做什么样的运动?
θ
m
若m、θ已知,则车的加速度多大?
θ
m
小车下滑的加速度为多大时系小球的细线刚好与斜面垂直?
A
B
C
D
F
5.四个相同的木块并排放在光滑的水平地面上,
当用力F推A使它们共同加速运动时,
A对B的作用力是多少?
6.如图所示,在光滑的地面上,水平外力F拉动小车和木块一起做加速运动,小车质量为M,木块质量为m,设加速度大小为a,木块和小车之间的动摩擦因数为?,则在这个过程中,木块受到的摩擦力大小是:
M
m
a
F
A,?mg
B.ma
C,mF/(M+m)
D,F-Ma
7.如图:m1>m2,滑轮质量和摩擦不计,则当将两物体由静止释放后,弹簧秤的读数是多少?
M1
M2
8.在气垫导轨上用不可伸缩的细绳,一端系在质量为m1
的滑块上,另一端系在质量为m2
的钩码上,如图所示。设导轨与滑块之间、细绳与滑轮之间
无摩擦,求滑块的加速度以及细绳的拉力。
m1
m2
a
a
牛顿第二定律的应用
一、
从受力确定运动情况
已知物体受力情况确定运动情况,指的是在受力情况已知的条件下,要求判断出物体的运动状态或求出物体的速度、位移等。
处理这类问题的基本思路是:先分析物体受力情况求合力,据牛顿第二定律求加速度,再用运动学公式求所求量(运动学量)。
物体运
动情况
运动学
公
式
加速度
a
牛顿第
二定律
物体受
力情况
二、从运动情况确定受力
已知物体运动情况确定受力情况,指的是在运动情况(知道三个运动学量)已知的条件下,要求得出物体所受的力或者相关物理量(如动摩擦因数等)。
处理这类问题的基本思路是:先分析物体的运动情况,据运动学公式求加速度,再在分析物体受力情况的基础上,用牛顿第二定律列方程求所求量(力)。
物体运
动情况
运动学
公
式
加速度
a
牛顿第
二定律
物体受
力情况
解:木箱受力如图:将F正交分解,则:
一木箱质量为m=10Kg,与水平地面间的动摩擦因数为μ=0.2,现用斜向右下方F=100N的力推木箱,使木箱在水平面上做匀加速运动。F与水平方向成θ=37O角,求经过t=5秒时木箱的速度。
FN
mg
Ff
F
θ
F1
F2
F2=
F
sinθ
②
F1=
F
cosθ
①
Ff=μFN
⑤
由①②③④⑤
⑥得
竖直方向:
③
水平方向:
④
v
=at
⑥
代入数据可得:
v
=24m/s
一个滑雪的人,质量m=75kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=30°,在t=5s的时间内滑下的路程S=60m,求滑雪人受到的阻力(包括摩擦和空气阻力)。
θ
F2
F1
θ
mg
F阻
FN
F1=
mgsinθ
②
根据牛顿第二定律:F1-F阻=m
a
③
1
2
由S=v0
t+at2
得
a
=
t2
2(S-v0t)
由①②③
得F阻=F1-ma
=
mgsinθ-
t2
2
m(S-v0t)
已知运动情况求受力情况
F阻
方向沿斜面向上
滑雪的人滑雪时受力如图,将G分解得:
代入数据可得:
F阻=67.5N
1
一木箱质量为m,与水平地面间的动摩擦因数为μ,现用斜向右下方与水平方向成θ角的力F推木箱,求从静止开始经过
t
秒时木箱的速度?
G
N
f
θ
Vt=?
V0=
0
F
Fcosθ
Fsinθ
竖直方向
N–
Fsinθ
=
G???①
水平方向
Fcosθ-
f
=
ma??
②
二者联系
f=μN?????????????
③
如果还要求经过
t
秒时木箱的速度vt=a
t
连结体问题:
连结体:两个(或两个以上)物体相互连 结参与运动的系统。
隔离法,整体法
光滑的水平面上有质量分别为m1、m2的两物体
静止靠在一起(如图)
,现对m1施加一个大小为
F
方向向右的推力作用。求此时物体m2受到物体
m1的作用力F1
m1
m2
F
[m1]
F
F1
[m2]
F1
FN1
[
解法一
]:
分别以m1、m2为隔离体作受力分析
FN2
m1g
m2g
对m1有
:F
–
F1
=
m
1a
(1)
对m2有:
F1
=
m2
a
(2)
联立(1)、(2)可得
F1
=
m1
m2
F
[m2]
F1
FN2
[
解法二
]:
对m1、m2视为整体作受力分析
m2g
有
:F
=
(m
1+
m2)a
(1)
对m2作受力分析
联立(1)、(2)可得
F1
=
FN
(m1
+
m2)g
F
有
:F1
=
m2
a
(2)
光滑的水平面上有质量分别为m1、m2的两物体
静止靠在一起(如图)
,现对m1施加一个大小为
F
方向向右的推力作用。求此时物体m2受到物体
m1的作用力F1
求m1对m2的作用力大小。
m1
m2
m2g
F1
FN
Ff
用水平推力F向左推
m1、m2间的作用力与原来相同吗?
对m2受力分析:
思考:
m
M
θ
F
例4.质量为M的斜面放置于水平面上,其上有质量为m
的小物块,各接触面均无摩擦力,将水平力
F加在M上,要求m与M不发生相对滑动,力F应为多大?
解:以m为对象;其受力如图:由图可得:
动
力
学
中
的
临
界
极
值
问
题
瞬时加速度的分析问题
分析物体在某一时刻的瞬时加速度,关键——分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
有两种模型:
①刚性绳(或接触面):是一种不需要发生明显形变就能产生弹力的物体,若剪断(或脱离)后,其中弹力立即发生变化,不需要形变恢复的时间。
②弹簧(或橡皮绳):特点是形变量大,形变恢复需要较长时间,在瞬时问题中,其弹力可以看成不变。
一条轻弹簧上端固定在天花板上,下端连接一物体A,A的下边通过一轻绳连接物体B。A、B的质量相同均为m,待平衡后剪断A、B间的细绳,则剪断细绳的瞬间,物体A、B加速度和方向?
A
B
A
B
如图,两个质量均为m的重物静止,若剪断绳OA,则剪断瞬间A和B的加速度分别是多少?
0
质量皆为m的A,B两球之间系着一个不计质量的轻弹簧,放在光滑水平台面上,A球紧靠墙壁,今用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间A,B的加速度分别为多少?
两物体P,Q分别固定在质量可以忽略不计的弹簧的两端,竖直放在一块水平板上并处于平衡状态,两物体的质量相等,如突然把平板撤开,在刚撤开的瞬间P,Q的加速度各是多少?
Q
P
如图,
质量为m的小球处于静止状态,若将绳剪断,则此瞬间小球的加速度是多少?
B
m
A
θ
如图所示,吊篮A、物体B、物体C的质量均为m,B和C分别固定在竖直弹簧两端,弹簧的质量不计.整个系统在轻绳悬挂下处于静止状态.现将悬挂吊篮的轻绳剪断,在轻绳刚断的瞬间( )
A.物体B的加速度大小为g
B.物体C的加速度大小为2g
C.吊篮A的加速度大小为3g
D.A、C间的弹力大小为0.5mg
D
可能一直加速
(2)可能先加速后匀速
⑴v0>v时,可能一直减速,也可能先减速再匀速
(2)v0<v时,可能一直加速,也可能先加速再匀速
传送带较短时,滑块一直减速达到左端
(2)传送带较长时,滑块还要被传送带传回右端.其中v0>v返回时速度为v,当v0<v返回时速度为v0
模型 传送带模型
可能一直加速
(2)可能先加速后匀速
⑴可能一直加速
(2)可能一直匀速
(3)可能先减速后反向加速
可能一直加速
(2)可能先加速后匀速
(3)可能先以a1加速后以a2加速
可能一直加速
(2)可能先加速后匀速
(3)可能一直匀速
(4)可能先以a1加速后以a2加速
模型 “等时圆”模型
图中的AB、AC、AD都是光滑的轨道,A、B、C、D四点在同一竖直圆周上,其中AD是竖直的。一小球从A点由静止开始,分别沿AB、AC、AD轨道滑下B、C、D点所用的时间分别为tl、t2、t3。则
A.tl=t2=t3
B.tl>t2>t3
C.tl
V0
θ
物体以某一初速度v0冲上倾角为θ的斜面,物体与斜面间的动摩擦因数为μ,则物体经多长时间上滑至最高点?
θ
小车的斜面光滑,倾角为θ,木块位于斜面上,则小车应以什么样的加速度运动才能使木块与它保持相对静止?
判断车在做什么样的运动?
θ
m
若m、θ已知,则车的加速度多大?
θ
m
小车下滑的加速度为多大时系小球的细线刚好与斜面垂直?
A
B
C
D
F
5.四个相同的木块并排放在光滑的水平地面上,
当用力F推A使它们共同加速运动时,
A对B的作用力是多少?
6.如图所示,在光滑的地面上,水平外力F拉动小车和木块一起做加速运动,小车质量为M,木块质量为m,设加速度大小为a,木块和小车之间的动摩擦因数为?,则在这个过程中,木块受到的摩擦力大小是:
M
m
a
F
A,?mg
B.ma
C,mF/(M+m)
D,F-Ma
7.如图:m1>m2,滑轮质量和摩擦不计,则当将两物体由静止释放后,弹簧秤的读数是多少?
M1
M2
8.在气垫导轨上用不可伸缩的细绳,一端系在质量为m1
的滑块上,另一端系在质量为m2
的钩码上,如图所示。设导轨与滑块之间、细绳与滑轮之间
无摩擦,求滑块的加速度以及细绳的拉力。
m1
m2
a
a
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
