2019-2020学年山东省聊城市东阿县七年级(下)期末数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省聊城市东阿县七年级(下)期末数学试卷 (word版,含解析) |

|
|
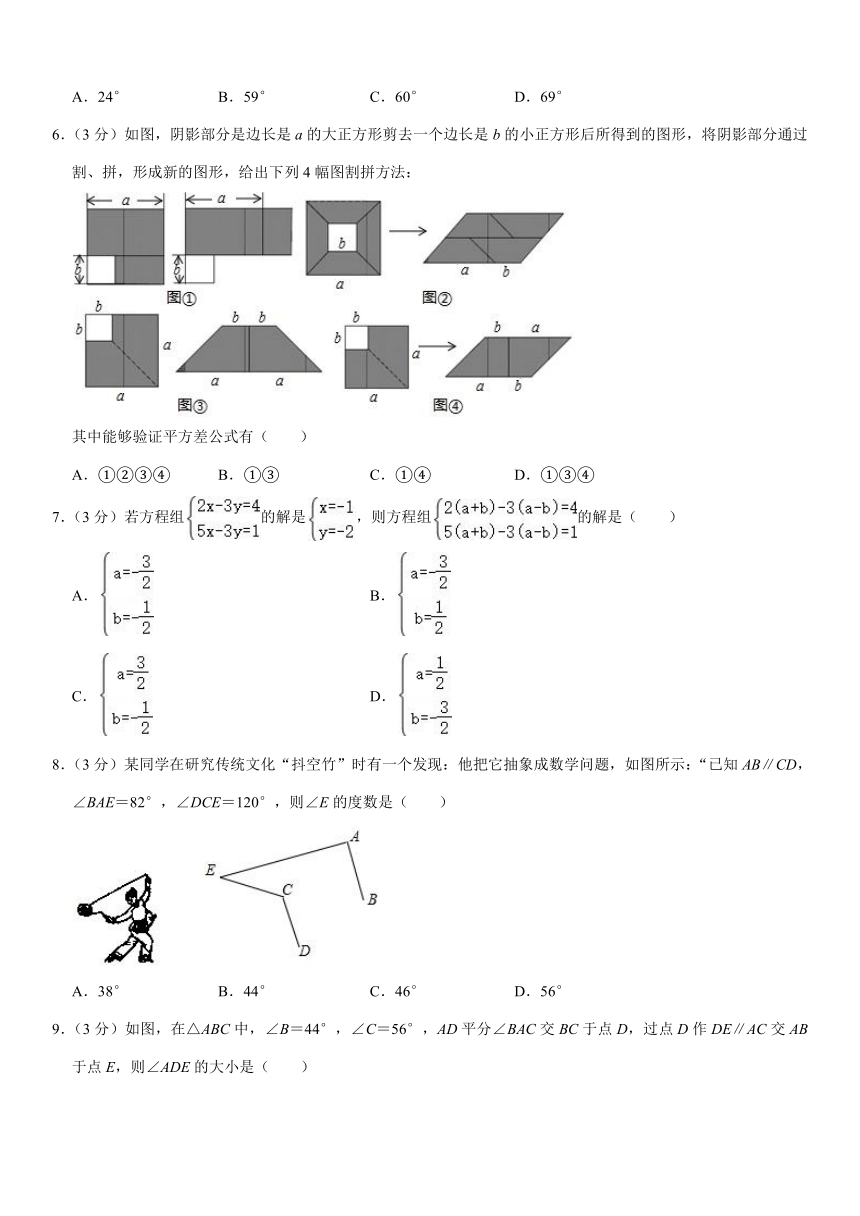
| 格式 | docx | ||
| 文件大小 | 310.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 00:00:00 | ||
图片预览




文档简介
2019-2020学年山东省聊城市东阿县七年级(下)期末数学试卷
一、选择题(本题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符题目要求)
1.(3分)下列计算正确的是( )
A.a6+a6=2a12
B.2﹣2÷20×23=32
C.(﹣ab2)?(﹣2a2b)3=a3b3
D.a3?(﹣a)5?a12=﹣a20
2.(3分)如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD+∠1=180° D.∠EOD=75°30'
3.(3分)如图,若点E的坐标为(﹣1,1),点F的坐标为(2,﹣1),则点G的坐标为( )
A.(2,0) B.(2,2) C.(0,2) D.(2,1)
4.(3分)已知某花粉直径为360000纳米(1米=109纳米),用科学记数法表示该花粉的直径是( )
A.3.6×105米 B.3.6×10﹣5米 C.3.6×10﹣4米 D.3.6×10﹣9米
5.(3分)如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
6.(3分)如图,阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列4幅图割拼方法:
其中能够验证平方差公式有( )
A.①②③④ B.①③ C.①④ D.①③④
7.(3分)若方程组的解是,则方程组的解是( )
A. B.
C. D.
8.(3分)某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:“已知AB∥CD,∠BAE=82°,∠DCE=120°,则∠E的度数是( )
A.38° B.44° C.46° D.56°
9.(3分)如图,在△ABC中,∠B=44°,∠C=56°,AD平分∠BAC交BC于点D,过点D作DE∥AC交AB于点E,则∠ADE的大小是( )
A.40° B.44° C.50° D.56°
10.(3分)我国古代数学著作《九章算术》卷七“盈不足”中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:几个人合伙买一件物品,每人出8元,则余3元;若每人出7元,则少4元,问几人合买?这件物品多少钱?若设有x人合买,这件物品y元,则根据题意列出的二元一次方程组为( )
A. B.
C. D.
11.(3分)如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
12.(3分)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2018,0) B.(2017,1) C.(2019,1) D.(2019,2)
二、填空题(本题共5个小题,每小题3分,共15分,只要求写出最后结果)
13.(3分)若2m=8,2n=32,则22m+n﹣4= .
14.(3分)在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形.
15.(3分)已知关于x,y的二元一次方程组与方程组的解相同,则2a﹣b= .
16.(3分)如图,六边形ABCDEF是正六边形,若l1∥l2,则∠1﹣∠2= .
17.(3分)在平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 .
三、解答题(本大题共7个小题,共69分.解答要写出必要的文字说明或演算步骤)
18.(8分)因式分解
(1)16x4﹣1;
(2)x2y﹣2xy2+y3;
(3)(x2+16y2)2﹣64x2y2;
(4)(a﹣b)(x﹣y)﹣(b﹣a)(x+y).
19.(8分)计算题
(1)(﹣2a2b)2?(﹣2a2b2)3;
(2)(﹣x)2?x3?(﹣2y)3﹣(﹣2xy)2?(﹣3x)3y;
(3)(x+y)(x2﹣xy+y2);
(4)(2t+3)(2t﹣3)﹣(4t+1)(t﹣9).
20.(8分)解下列方程组
(1);
(2).
21.(8分)甲、乙两人分别计算(3x+a)(4x+b).甲抄错a的符号,得到结果是12x2+17x+6,乙漏抄第二个括号中x的系数,得到结果是3x2+7x﹣6,问:
(1)a,b分别是多少?
(2)该题的正确答案是多少?
22.(8分)如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.
23.(9分)【阅读材料】
某地铁公司规定:自2019年3月31日起,普通成人持储值卡乘坐地铁出行,每个自然月内,达到规定消费累计金额后的乘次,享受相应的折扣优惠(见图).地铁出行消费累计金额月底清零,次月重新累计.
比如:李老师二月份无储值卡消费260元,若采用新规持储值卡消费,则需付费150×0.95+50×0.9+60×0.8=235.5元;
【解决问题】
甲,乙两个成人二月份无储值卡乘坐地铁消费金额合计300元(甲消费金额超过150元,但不超过200元).若两人采用新规持储值卡消费,则共需付费283.5元.求甲、乙二月份乘坐地铁的消费金额各是多少元?
24.(8分)如图,AB∥CD,点E在线段AB上,连接EC、ED、AD,且AD⊥CE于F,ED平分∠CEB,若∠ADC=40°,∠A﹣∠B=10°,求∠BDE的度数.
25.(12分)已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP的面积为△ABC面积的两倍,求点P的坐标.
2019-2020学年山东省聊城市东阿县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符题目要求)
1.【答案】D
【解答】解:A、a6+a6=2a6,故此选项错误;
B、2﹣8÷20×63=2,故此选项错误;
C、(﹣ab2)?(﹣2a2b)3=(﹣ab2)?(﹣8a6b8)=4a7b5,故此选项错误;
D、a3?(﹣a)5?a12=﹣a20,正确.
故选:D.
2.【答案】D
【解答】解:A、由OE⊥AB,可知∠AOE=90°,OF平分∠AOE,则∠2=45°,正确;
B、∠1与∠3互为对顶角,因而相等,正确;
C、∠AOD与∠3互为邻补角,正确;
D、∠EOD=180°﹣15°30'﹣45°≠75°30',错误;
故选:D.
3.【答案】B
【解答】解:如图所示:
点G的坐标为(2,2),
故选:B.
4.【答案】C
【解答】解:360000纳米=360000×10﹣9m=3.6×10﹣4米.
故选:C.
5.【答案】B
【解答】解:∵∠A=35°,∠C=24°,
∴∠DBC=∠A+∠C=59°,
∴∠D=∠DBC=59°,
故选:B.
6.【答案】A
【解答】解:图①,左边图形的阴影部分的面积=a2﹣b2,右边图形阴影部分的面积=(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),故①可以验证平方差公式;
∴a3﹣b2=(a+b)(a﹣b),故②可以验证平方差公式;
∴a2﹣b2=(a+b)(a﹣b),故③可以验证平方差公式;
∴a2﹣b2=(a+b)(a﹣b),故④可以验证平方差公式.
故选:A.
7.【答案】B
【解答】解:由题意得:,
解得:,
故选:B.
8.【答案】A
【解答】解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=82°,
又∵∠DCE=120°,
故选:A.
9.【答案】A
【解答】解:∵∠BAC=180°﹣∠B﹣∠C,∠B=44°,∠C=56°,
∴∠BAC=80°,
∴∠DAC=∠BAC=40°,
∴∠ADE=∠DAC=40°,
故选:A.
10.【答案】D
【解答】解:由题意可得:,
故选:D.
11.【答案】A
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∵∠BOD+∠BOM=180°,
故选:A.
12.【答案】D
【解答】解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3,
故选:D.
二、填空题(本题共5个小题,每小题3分,共15分,只要求写出最后结果)
13.【答案】128.
【解答】解:∵2m=8,2n=32,
∴24m+n﹣4=(2m)2×2n÷24
=128.
故答案为:128.
14.【答案】12.
【解答】解:∵正方形的一个内角度数为180°×(4﹣2)÷4=90°,正六边形的一个内角度数为180°×(6﹣2)÷6=120°,
∴需要的多边形的一个内角度数为360°﹣90°﹣120°=150°,
∴第三个正多边形的边数为360÷30=12,
故答案为:12.
15.【答案】见试题解答内容
【解答】解:
解得:
得:
故答案为:4
16.【答案】见试题解答内容
【解答】解:如图,过A作l∥l1,则∠4=∠2,
∵六边形ABCDEF是正六边形,
∴∠5+∠3=120°,即∠3=120°﹣∠2,
∴l∥l2,
∴∠1+120°﹣∠2=180°,
故答案为:60°.
17.【答案】2,(3,2).
【解答】解:依题意可得:
∴y=2,
点B到AC的距离最短,即BC的最小值=4﹣2=3,
故答为:2,(3,2).
三、解答题(本大题共7个小题,共69分.解答要写出必要的文字说明或演算步骤)
18.【答案】(1)(4x2+1)(2x+1)(2x﹣1);
(2)y(x﹣y)2;
(3)(x+4y)2(x﹣4y)2;
(4)2x(a﹣b).
【解答】解:(1)原式=(4x2+6)(4x2﹣1)
=(4x2+1)(2x+1)(2x﹣1);
=y(x﹣y)4;
=(x+4y)2(x﹣4y)2;
=(a﹣b)(x﹣y+x+y)
=2x(a﹣b).
19.【答案】(1)﹣32a10b8;
(2)100x5y3;
(3)x3+y3;
(4)35t.
【解答】解:(1)原式=4a4b2?(﹣8a6b5)
=﹣32a10b8;
(3)原式=x3﹣x2y+xy2+x6y﹣xy2+y3
(4)原式=4t6﹣9﹣(4t2﹣35t﹣9)
=35t.
20.【答案】(1);(2).
【解答】解:(1),
①×3+②,可得8m=12,
把m=1.5代入①,解得n=3,
(2)由,
①+②×11,可得16x=﹣100,
把x=﹣代入②,解得y=﹣,
∴原方程组的解是.
21.【答案】见试题解答内容
【解答】解:(1)∵乙漏抄第二个括号中x的系数,得到结果是3x2+5x﹣6,
∴(3x+a)(x+b)=3x2+3x﹣6,
∴3b+a=7,
∴(3x﹣a)(4x+b)=12x6+17x+6,
∴3b﹣4a=17,
解得:a=﹣2,b=3.
=(8x﹣2)(4x+3)
=12x2+x﹣6.
22.【答案】见试题解答内容
【解答】解:∵EP⊥EF,
∴∠PEM=90°,∠PEF=90°.
∴∠BEM=∠PEM﹣∠BEP=90°﹣40°=50°.
∴∠BEM=∠EFD=50°.
∴∠EFP=∠EFD=25°,
∴∠P=90°﹣25°=65°.
23.【答案】见试题解答内容
【解答】解:甲二月份乘坐地铁的消费金额是x元,
乙二月份乘坐地铁的消费金额是y元,
答:甲、乙二月份乘坐地铁的消费金额各是180元、120元.
24.【答案】见试题解答内容
【解答】解:∵AB∥CD,
∴∠ADC=∠A=40°,
∴∠B=30°,
∴∠AFE=90°,
∴∠BEC=130°,
∴∠BED=∠BEC=65°,
∴∠BDE=180°﹣30°﹣65°=85°.
25.【答案】见试题解答内容
【解答】解:(1)△ABC如图所示;
∴S△ABC=S四边形CEOF﹣S△AEC﹣S△AOB﹣S△BCF
=4.
∴BP=16,
当点P在y轴上时,△ABP的面积=?OB?AP=2,
∴P(0,9)或(0,﹣7),
综上所述,满足条件的点P坐标为(18,2)或(﹣14,0)或(0,9)或(0,﹣4).
一、选择题(本题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符题目要求)
1.(3分)下列计算正确的是( )
A.a6+a6=2a12
B.2﹣2÷20×23=32
C.(﹣ab2)?(﹣2a2b)3=a3b3
D.a3?(﹣a)5?a12=﹣a20
2.(3分)如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD+∠1=180° D.∠EOD=75°30'
3.(3分)如图,若点E的坐标为(﹣1,1),点F的坐标为(2,﹣1),则点G的坐标为( )
A.(2,0) B.(2,2) C.(0,2) D.(2,1)
4.(3分)已知某花粉直径为360000纳米(1米=109纳米),用科学记数法表示该花粉的直径是( )
A.3.6×105米 B.3.6×10﹣5米 C.3.6×10﹣4米 D.3.6×10﹣9米
5.(3分)如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
6.(3分)如图,阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列4幅图割拼方法:
其中能够验证平方差公式有( )
A.①②③④ B.①③ C.①④ D.①③④
7.(3分)若方程组的解是,则方程组的解是( )
A. B.
C. D.
8.(3分)某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:“已知AB∥CD,∠BAE=82°,∠DCE=120°,则∠E的度数是( )
A.38° B.44° C.46° D.56°
9.(3分)如图,在△ABC中,∠B=44°,∠C=56°,AD平分∠BAC交BC于点D,过点D作DE∥AC交AB于点E,则∠ADE的大小是( )
A.40° B.44° C.50° D.56°
10.(3分)我国古代数学著作《九章算术》卷七“盈不足”中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:几个人合伙买一件物品,每人出8元,则余3元;若每人出7元,则少4元,问几人合买?这件物品多少钱?若设有x人合买,这件物品y元,则根据题意列出的二元一次方程组为( )
A. B.
C. D.
11.(3分)如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
12.(3分)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2018,0) B.(2017,1) C.(2019,1) D.(2019,2)
二、填空题(本题共5个小题,每小题3分,共15分,只要求写出最后结果)
13.(3分)若2m=8,2n=32,则22m+n﹣4= .
14.(3分)在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形.
15.(3分)已知关于x,y的二元一次方程组与方程组的解相同,则2a﹣b= .
16.(3分)如图,六边形ABCDEF是正六边形,若l1∥l2,则∠1﹣∠2= .
17.(3分)在平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 .
三、解答题(本大题共7个小题,共69分.解答要写出必要的文字说明或演算步骤)
18.(8分)因式分解
(1)16x4﹣1;
(2)x2y﹣2xy2+y3;
(3)(x2+16y2)2﹣64x2y2;
(4)(a﹣b)(x﹣y)﹣(b﹣a)(x+y).
19.(8分)计算题
(1)(﹣2a2b)2?(﹣2a2b2)3;
(2)(﹣x)2?x3?(﹣2y)3﹣(﹣2xy)2?(﹣3x)3y;
(3)(x+y)(x2﹣xy+y2);
(4)(2t+3)(2t﹣3)﹣(4t+1)(t﹣9).
20.(8分)解下列方程组
(1);
(2).
21.(8分)甲、乙两人分别计算(3x+a)(4x+b).甲抄错a的符号,得到结果是12x2+17x+6,乙漏抄第二个括号中x的系数,得到结果是3x2+7x﹣6,问:
(1)a,b分别是多少?
(2)该题的正确答案是多少?
22.(8分)如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.
23.(9分)【阅读材料】
某地铁公司规定:自2019年3月31日起,普通成人持储值卡乘坐地铁出行,每个自然月内,达到规定消费累计金额后的乘次,享受相应的折扣优惠(见图).地铁出行消费累计金额月底清零,次月重新累计.
比如:李老师二月份无储值卡消费260元,若采用新规持储值卡消费,则需付费150×0.95+50×0.9+60×0.8=235.5元;
【解决问题】
甲,乙两个成人二月份无储值卡乘坐地铁消费金额合计300元(甲消费金额超过150元,但不超过200元).若两人采用新规持储值卡消费,则共需付费283.5元.求甲、乙二月份乘坐地铁的消费金额各是多少元?
24.(8分)如图,AB∥CD,点E在线段AB上,连接EC、ED、AD,且AD⊥CE于F,ED平分∠CEB,若∠ADC=40°,∠A﹣∠B=10°,求∠BDE的度数.
25.(12分)已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP的面积为△ABC面积的两倍,求点P的坐标.
2019-2020学年山东省聊城市东阿县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符题目要求)
1.【答案】D
【解答】解:A、a6+a6=2a6,故此选项错误;
B、2﹣8÷20×63=2,故此选项错误;
C、(﹣ab2)?(﹣2a2b)3=(﹣ab2)?(﹣8a6b8)=4a7b5,故此选项错误;
D、a3?(﹣a)5?a12=﹣a20,正确.
故选:D.
2.【答案】D
【解答】解:A、由OE⊥AB,可知∠AOE=90°,OF平分∠AOE,则∠2=45°,正确;
B、∠1与∠3互为对顶角,因而相等,正确;
C、∠AOD与∠3互为邻补角,正确;
D、∠EOD=180°﹣15°30'﹣45°≠75°30',错误;
故选:D.
3.【答案】B
【解答】解:如图所示:
点G的坐标为(2,2),
故选:B.
4.【答案】C
【解答】解:360000纳米=360000×10﹣9m=3.6×10﹣4米.
故选:C.
5.【答案】B
【解答】解:∵∠A=35°,∠C=24°,
∴∠DBC=∠A+∠C=59°,
∴∠D=∠DBC=59°,
故选:B.
6.【答案】A
【解答】解:图①,左边图形的阴影部分的面积=a2﹣b2,右边图形阴影部分的面积=(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),故①可以验证平方差公式;
∴a3﹣b2=(a+b)(a﹣b),故②可以验证平方差公式;
∴a2﹣b2=(a+b)(a﹣b),故③可以验证平方差公式;
∴a2﹣b2=(a+b)(a﹣b),故④可以验证平方差公式.
故选:A.
7.【答案】B
【解答】解:由题意得:,
解得:,
故选:B.
8.【答案】A
【解答】解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=82°,
又∵∠DCE=120°,
故选:A.
9.【答案】A
【解答】解:∵∠BAC=180°﹣∠B﹣∠C,∠B=44°,∠C=56°,
∴∠BAC=80°,
∴∠DAC=∠BAC=40°,
∴∠ADE=∠DAC=40°,
故选:A.
10.【答案】D
【解答】解:由题意可得:,
故选:D.
11.【答案】A
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∵∠BOD+∠BOM=180°,
故选:A.
12.【答案】D
【解答】解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3,
故选:D.
二、填空题(本题共5个小题,每小题3分,共15分,只要求写出最后结果)
13.【答案】128.
【解答】解:∵2m=8,2n=32,
∴24m+n﹣4=(2m)2×2n÷24
=128.
故答案为:128.
14.【答案】12.
【解答】解:∵正方形的一个内角度数为180°×(4﹣2)÷4=90°,正六边形的一个内角度数为180°×(6﹣2)÷6=120°,
∴需要的多边形的一个内角度数为360°﹣90°﹣120°=150°,
∴第三个正多边形的边数为360÷30=12,
故答案为:12.
15.【答案】见试题解答内容
【解答】解:
解得:
得:
故答案为:4
16.【答案】见试题解答内容
【解答】解:如图,过A作l∥l1,则∠4=∠2,
∵六边形ABCDEF是正六边形,
∴∠5+∠3=120°,即∠3=120°﹣∠2,
∴l∥l2,
∴∠1+120°﹣∠2=180°,
故答案为:60°.
17.【答案】2,(3,2).
【解答】解:依题意可得:
∴y=2,
点B到AC的距离最短,即BC的最小值=4﹣2=3,
故答为:2,(3,2).
三、解答题(本大题共7个小题,共69分.解答要写出必要的文字说明或演算步骤)
18.【答案】(1)(4x2+1)(2x+1)(2x﹣1);
(2)y(x﹣y)2;
(3)(x+4y)2(x﹣4y)2;
(4)2x(a﹣b).
【解答】解:(1)原式=(4x2+6)(4x2﹣1)
=(4x2+1)(2x+1)(2x﹣1);
=y(x﹣y)4;
=(x+4y)2(x﹣4y)2;
=(a﹣b)(x﹣y+x+y)
=2x(a﹣b).
19.【答案】(1)﹣32a10b8;
(2)100x5y3;
(3)x3+y3;
(4)35t.
【解答】解:(1)原式=4a4b2?(﹣8a6b5)
=﹣32a10b8;
(3)原式=x3﹣x2y+xy2+x6y﹣xy2+y3
(4)原式=4t6﹣9﹣(4t2﹣35t﹣9)
=35t.
20.【答案】(1);(2).
【解答】解:(1),
①×3+②,可得8m=12,
把m=1.5代入①,解得n=3,
(2)由,
①+②×11,可得16x=﹣100,
把x=﹣代入②,解得y=﹣,
∴原方程组的解是.
21.【答案】见试题解答内容
【解答】解:(1)∵乙漏抄第二个括号中x的系数,得到结果是3x2+5x﹣6,
∴(3x+a)(x+b)=3x2+3x﹣6,
∴3b+a=7,
∴(3x﹣a)(4x+b)=12x6+17x+6,
∴3b﹣4a=17,
解得:a=﹣2,b=3.
=(8x﹣2)(4x+3)
=12x2+x﹣6.
22.【答案】见试题解答内容
【解答】解:∵EP⊥EF,
∴∠PEM=90°,∠PEF=90°.
∴∠BEM=∠PEM﹣∠BEP=90°﹣40°=50°.
∴∠BEM=∠EFD=50°.
∴∠EFP=∠EFD=25°,
∴∠P=90°﹣25°=65°.
23.【答案】见试题解答内容
【解答】解:甲二月份乘坐地铁的消费金额是x元,
乙二月份乘坐地铁的消费金额是y元,
答:甲、乙二月份乘坐地铁的消费金额各是180元、120元.
24.【答案】见试题解答内容
【解答】解:∵AB∥CD,
∴∠ADC=∠A=40°,
∴∠B=30°,
∴∠AFE=90°,
∴∠BEC=130°,
∴∠BED=∠BEC=65°,
∴∠BDE=180°﹣30°﹣65°=85°.
25.【答案】见试题解答内容
【解答】解:(1)△ABC如图所示;
∴S△ABC=S四边形CEOF﹣S△AEC﹣S△AOB﹣S△BCF
=4.
∴BP=16,
当点P在y轴上时,△ABP的面积=?OB?AP=2,
∴P(0,9)或(0,﹣7),
综上所述,满足条件的点P坐标为(18,2)或(﹣14,0)或(0,9)或(0,﹣4).
同课章节目录
