北师大版三年级数学上册5.1 什么是周长(16张ppt)
文档属性
| 名称 | 北师大版三年级数学上册5.1 什么是周长(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 563.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 14:01:24 | ||
图片预览





文档简介
5.1 什么是周长
五 周 长
学习目标
1.结合具体实物或图形,在观察、思考、操作等活动中,认识物体表面或图形的周长。
2.会计算多边形的周长,并能寻求简单合理的运算途径。
3.能与他人合作,测量物体表面或简单图形的周长,获得测量周长的活动经验,感受周长与实际生活的密切联系,并发展合作技能。
回顾复习
口算。
20
2100
200
300
90
32
100÷5=
300×7=
40×5=
2700÷9=
360÷4=
96÷3=
例题解读
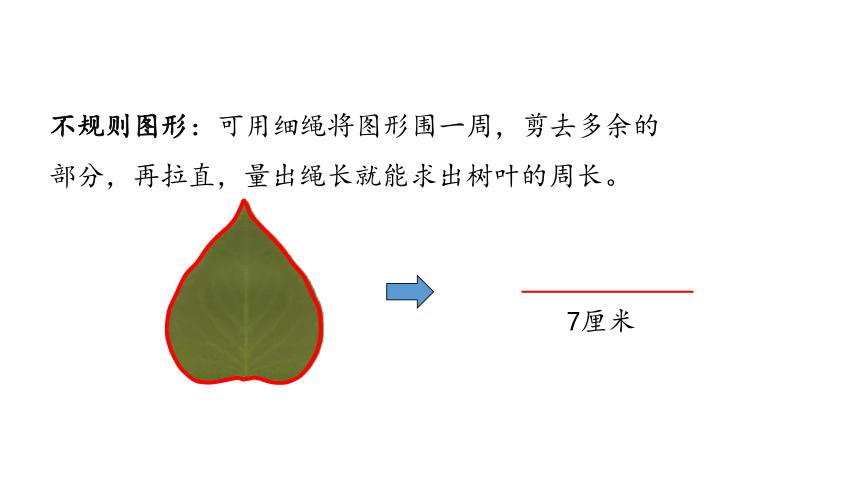
用彩笔描出树叶和数学书封面的边线。
你能得到树叶和数学书封面的周长吗?
7厘米
不规则图形:可用细绳将图形围一周,剪去多余的部分,再拉直,量出绳长就能求出树叶的周长。
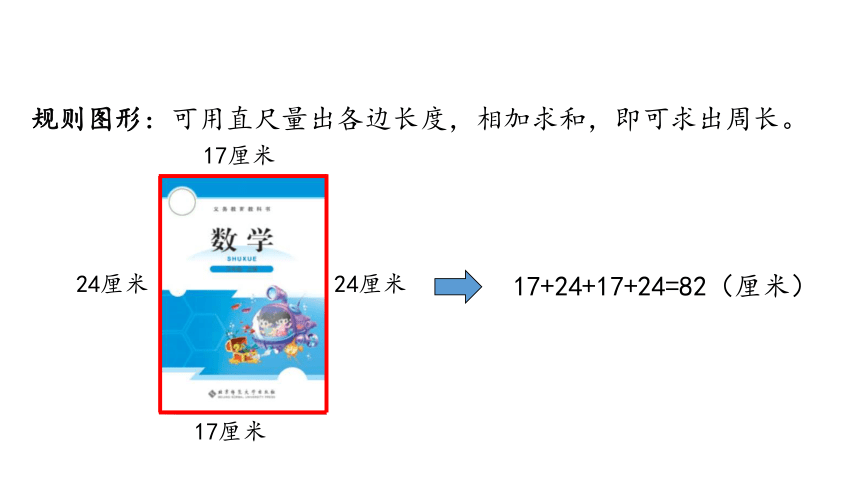
规则图形:可用直尺量出各边长度,相加求和,即可求出周长。
24厘米
17厘米
24厘米
17厘米
17+24+17+24=82(厘米)
1厘米
1厘米
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
20厘米
18厘米
30厘米
数一数,下面图形的周长分别是多少厘米?
方法一:240+410+200+190+560=1600(米)
方法二:190+410=600(米)
560+240=800(米)
600+800+200=1600(米)
一条小路环绕着一个小公园,小公园的周长是多少?
答:小公园的周长是1600米。
120×3=360(米)
(110+90)+(124+86)=410(米)
75×4+100=400(米)
求出下面图形的周长。
典型例题
笑笑在动物园里沿着右面这条路线走了一周,她一共走了多少米?
(170+230)+(140+160)+200=900(米)
提示:为了计算简单,凑成整百数的一起算。
答:她一共走了900米。
小结
周 长
(1)封闭图形一周的长度,是它的周长。
(2)测量图形的周长时,规则图形可采用直尺测量法,不规则图形可采用绕绳法。
随堂小测
1.下面图形的周长是多少?
6厘米
3厘米
4厘米
2厘米
2厘米
3厘米
3厘米
1厘米
3厘米
2厘米
2厘米
6+4+3=13(厘米)
2+3+2+3=10(厘米)
2+1+2+3=8(厘米)
2.下图是一个公园的示意图。王奶奶绕着公园走一圈是多少米?
20+150+100+180+80=530(米)
答:王奶奶绕着公园走一圈是530米。
3.下面图形的周长一样吗?为什么?
一样,因为一周的长度相等。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
五 周 长
学习目标
1.结合具体实物或图形,在观察、思考、操作等活动中,认识物体表面或图形的周长。
2.会计算多边形的周长,并能寻求简单合理的运算途径。
3.能与他人合作,测量物体表面或简单图形的周长,获得测量周长的活动经验,感受周长与实际生活的密切联系,并发展合作技能。
回顾复习
口算。
20
2100
200
300
90
32
100÷5=
300×7=
40×5=
2700÷9=
360÷4=
96÷3=
例题解读
用彩笔描出树叶和数学书封面的边线。
你能得到树叶和数学书封面的周长吗?
7厘米
不规则图形:可用细绳将图形围一周,剪去多余的部分,再拉直,量出绳长就能求出树叶的周长。
规则图形:可用直尺量出各边长度,相加求和,即可求出周长。
24厘米
17厘米
24厘米
17厘米
17+24+17+24=82(厘米)
1厘米
1厘米
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
20厘米
18厘米
30厘米
数一数,下面图形的周长分别是多少厘米?
方法一:240+410+200+190+560=1600(米)
方法二:190+410=600(米)
560+240=800(米)
600+800+200=1600(米)
一条小路环绕着一个小公园,小公园的周长是多少?
答:小公园的周长是1600米。
120×3=360(米)
(110+90)+(124+86)=410(米)
75×4+100=400(米)
求出下面图形的周长。
典型例题
笑笑在动物园里沿着右面这条路线走了一周,她一共走了多少米?
(170+230)+(140+160)+200=900(米)
提示:为了计算简单,凑成整百数的一起算。
答:她一共走了900米。
小结
周 长
(1)封闭图形一周的长度,是它的周长。
(2)测量图形的周长时,规则图形可采用直尺测量法,不规则图形可采用绕绳法。
随堂小测
1.下面图形的周长是多少?
6厘米
3厘米
4厘米
2厘米
2厘米
3厘米
3厘米
1厘米
3厘米
2厘米
2厘米
6+4+3=13(厘米)
2+3+2+3=10(厘米)
2+1+2+3=8(厘米)
2.下图是一个公园的示意图。王奶奶绕着公园走一圈是多少米?
20+150+100+180+80=530(米)
答:王奶奶绕着公园走一圈是530米。
3.下面图形的周长一样吗?为什么?
一样,因为一周的长度相等。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
