北师大版七年级上册数学 4.3角 课件(17张)
文档属性
| 名称 | 北师大版七年级上册数学 4.3角 课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 13:30:29 | ||
图片预览





文档简介
1.理解角以及平角、周角的概念
2.掌握角的表示方法。
3.掌握角的常用度量单位:度、分、秒,及他们之间的换算关系,并会进行简单的换算。
1.角及相关的概念
2.角的表示方法
3.角的度量单位
以一点为端点画两条射线
组成的图形是什么?
这个图形有什么特征?
观察并思考:
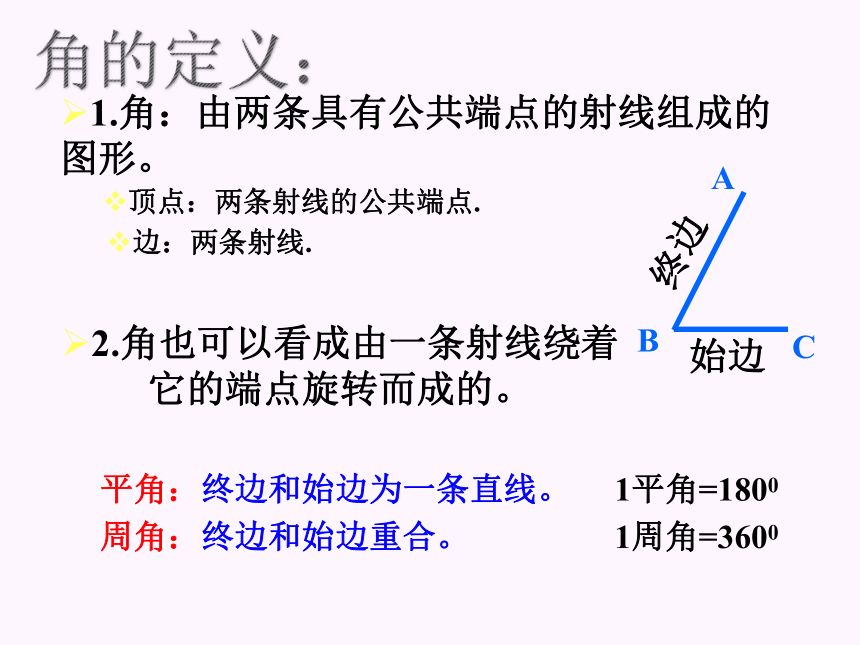
1.角:由两条具有公共端点的射线组成的 图形。
顶点:两条射线的公共端点.
边:两条射线.
始边
终边
2.角也可以看成由一条射线绕着 它的端点旋转而成的。
B
A
C
平角:终边和始边为一条直线。
1平角=1800
1周角=3600
周角:终边和始边重合。
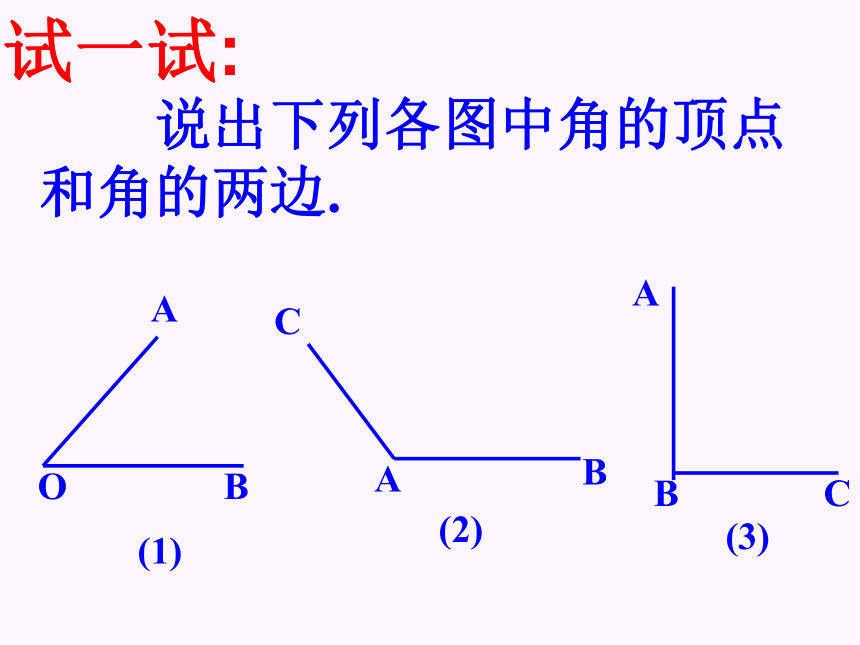
说出下列各图中角的顶点和角的两边.
A
B
O
B
C
A
A
B
C
(1)
(3)
(2)
试一试:
A
B
C
角的表示方法:
1、用符号“∠”及三个大写英文字母来表示.如:
2、当为一个单独的角时,可用符号“∠”及一个大写英文字母来表示.如:
3、用符号“∠”及一个数字来表示.如:
4、用符号“∠”及一个希腊字母(α、β、γ...)来表示.
∠ABC
A
B
C
∠B
A
B
C
C
A
B
∠1
∠α
1
α
∠2
∠α
∠BCE
∠BAD
∠BAC
∠1
∠3
∠4
∠ABC
∠BCA
将图中的角用不同方法表示出来并填写下表
A
C
2
1
3
4
B
D
E
α
练一练:
做一做
如图, D、E分别是AB、AC上的点.
(1)∠ ABC与∠ DBC 。
(2)∠BAC与∠ DAE 。
(3)∠BAC与∠ ACB 。
D
E
A
C
B
图
O
A
D
E
C
B
图
1°的 为1分,
1
60
记作“1′”,
即1°=60′.
1′的 为1秒,
1
60
记作“1″”,
即1′=60″.
例1.计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′×1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″×87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
0.25°= 分= 秒
2700″= 分= 度
1
8
(
) °= 分= 秒
6000″= 分= 度
当堂检测:
45
0.75
15
900
7.5
450
100
5
3
1.角的概念(两种定义)
2.角的表示方法有四种
3.角的单位及其换算.
表示方法
图例
记法
适用范围
B
A
C
1
A
用三个大写字母表示
用一个大写字母表示
用数字表示
用希腊字母表示
∠CAB或∠BAC
∠A
∠1
∠α
任何情况都适用,表示顶点的字母必须写在中间
以这一点为顶点的角只有一个
任何情况都使用
任何情况都使用
α
确定相应钟表上时针与分针所成的角度。
120°
1、每经过1小时,时针转过多少度?
每经过1分钟,分针转过多少度?
思考:
2、八点半时,时针和分针的夹角是多少度?
5:25的时候,时针和分针的夹角是多少度?
2.掌握角的表示方法。
3.掌握角的常用度量单位:度、分、秒,及他们之间的换算关系,并会进行简单的换算。
1.角及相关的概念
2.角的表示方法
3.角的度量单位
以一点为端点画两条射线
组成的图形是什么?
这个图形有什么特征?
观察并思考:
1.角:由两条具有公共端点的射线组成的 图形。
顶点:两条射线的公共端点.
边:两条射线.
始边
终边
2.角也可以看成由一条射线绕着 它的端点旋转而成的。
B
A
C
平角:终边和始边为一条直线。
1平角=1800
1周角=3600
周角:终边和始边重合。
说出下列各图中角的顶点和角的两边.
A
B
O
B
C
A
A
B
C
(1)
(3)
(2)
试一试:
A
B
C
角的表示方法:
1、用符号“∠”及三个大写英文字母来表示.如:
2、当为一个单独的角时,可用符号“∠”及一个大写英文字母来表示.如:
3、用符号“∠”及一个数字来表示.如:
4、用符号“∠”及一个希腊字母(α、β、γ...)来表示.
∠ABC
A
B
C
∠B
A
B
C
C
A
B
∠1
∠α
1
α
∠2
∠α
∠BCE
∠BAD
∠BAC
∠1
∠3
∠4
∠ABC
∠BCA
将图中的角用不同方法表示出来并填写下表
A
C
2
1
3
4
B
D
E
α
练一练:
做一做
如图, D、E分别是AB、AC上的点.
(1)∠ ABC与∠ DBC 。
(2)∠BAC与∠ DAE 。
(3)∠BAC与∠ ACB 。
D
E
A
C
B
图
O
A
D
E
C
B
图
1°的 为1分,
1
60
记作“1′”,
即1°=60′.
1′的 为1秒,
1
60
记作“1″”,
即1′=60″.
例1.计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′×1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″×87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
0.25°= 分= 秒
2700″= 分= 度
1
8
(
) °= 分= 秒
6000″= 分= 度
当堂检测:
45
0.75
15
900
7.5
450
100
5
3
1.角的概念(两种定义)
2.角的表示方法有四种
3.角的单位及其换算.
表示方法
图例
记法
适用范围
B
A
C
1
A
用三个大写字母表示
用一个大写字母表示
用数字表示
用希腊字母表示
∠CAB或∠BAC
∠A
∠1
∠α
任何情况都适用,表示顶点的字母必须写在中间
以这一点为顶点的角只有一个
任何情况都使用
任何情况都使用
α
确定相应钟表上时针与分针所成的角度。
120°
1、每经过1小时,时针转过多少度?
每经过1分钟,分针转过多少度?
思考:
2、八点半时,时针和分针的夹角是多少度?
5:25的时候,时针和分针的夹角是多少度?
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
