高中数学选择性必修(第一册)知识讲义 空间向量基本定理及坐标表示-人教A版(2019)
文档属性
| 名称 | 高中数学选择性必修(第一册)知识讲义 空间向量基本定理及坐标表示-人教A版(2019) |
|
|
| 格式 | docx | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 00:00:00 | ||
图片预览



文档简介
空间向量基本定理及坐标表示
重点
1. 理解空间向量的基本定理及其意义;
2. 掌握空间向量的正交分解及其坐标表示。
难点
用不用的基底表示空间任一向量
考试要求
考试
题型 选择题、填空题、解答题
难度 中等
核心知识点一:空间向量基本定理
定理:如果三个向量false不共面,那么对任意一个空间向量false,存在唯一的有序实数组{x,y,z},使得false,其中false叫做空间的一个基底,false都叫做基向量。空间中任意三个不共面的向量都可以构成空间的一个基底。
核心知识点二:空间向量的正交分解
如果空间中的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用false表示。由空间向量基本定理可知,对空间中的任意向量false,均可以分解为三个向量false,使false。像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解。
注意:
(1)空间任意三个不共面的向量都可以作为空间向量的一个基底。
(2)false与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是false。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念。
核心知识点三:空间直角坐标系及向量坐标
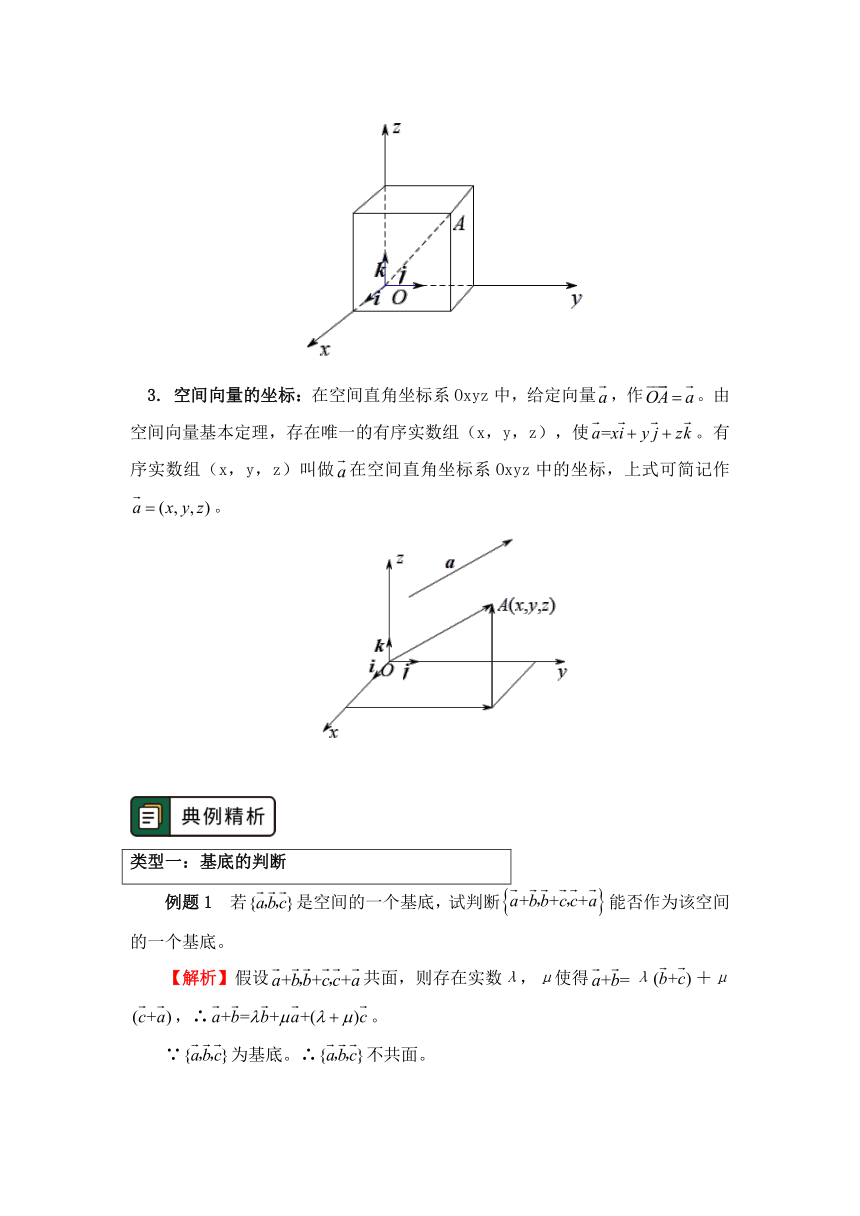
1. 空间直角坐标系:在空间选定一点O和一个单位正交基底false。以点O为原点,分别以false的方向为正方向,以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴。这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,false都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分。
教材中所用的坐标系都是右手直角坐标系,其规则是:让右手拇指指向x轴正方向,食指指向y轴正方向,则中指指向z轴正方向。
2. 空间点的坐标:数轴Ox上点M用实数x表示,直角坐标平面上的点M用一对有序实数(x,y)表示,建立空间直角坐标系后,空间的点M可用有序实数组(x,y,z)表示。
在空间直角坐标系Oxyz中,false为坐标向量,对空间任意一点A,对应一个向量false,且点A的位置由向量false唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使false。
在单位正交基底false下与向量false对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中z叫做A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标。
3. 空间向量的坐标:在空间直角坐标系Oxyz中,给定向量false,作false。由空间向量基本定理,存在唯一的有序实数组(x,y,z),使false。有序实数组(x,y,z)叫做false在空间直角坐标系Oxyz中的坐标,上式可简记作false。
类型一:基底的判断
例题1 若false是空间的一个基底,试判断false能否作为该空间的一个基底。
【解析】假设false共面,则存在实数λ,μ使得falseλfalse+μfalse,∴false。
∵false为基底。∴false不共面。
∴false此方程组无解,∴false不共面。
∴false可以作为空间的一个基底。
总结提升:
判断给出的某一向量组能否作为基底,关键是要判断它们是否共面。如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断。
类型二:用基底表示向量
例题2 四棱锥P-OABC的底面为一矩形,PO⊥平面OABC。设false=false,false=false,false=false,E,F分别是PC和PB的中点,试用false,false,false表示false,false,false,false。
【解析】连接BO,则false=falsefalse=false(false+false)=false(false+false+false)=false(false-false-false)=-falsefalse-falsefalse+falsefalse。
false=false+false=-false+falsefalse=-false+false(false+false)=-false-falsefalse+falsefalse。
false=false+false=false+false+false(false+false)=-false+false+false(-false+false)=-false+falsefalse+falsefalse。
false=falsefalse=falsefalse=falsefalse。
总结提升:
用基底表示空间向量一般要用到向量的加法、减法、数乘的运算,包括平行四边形法则及三角形法则。
类型三:用坐标表示空间向量
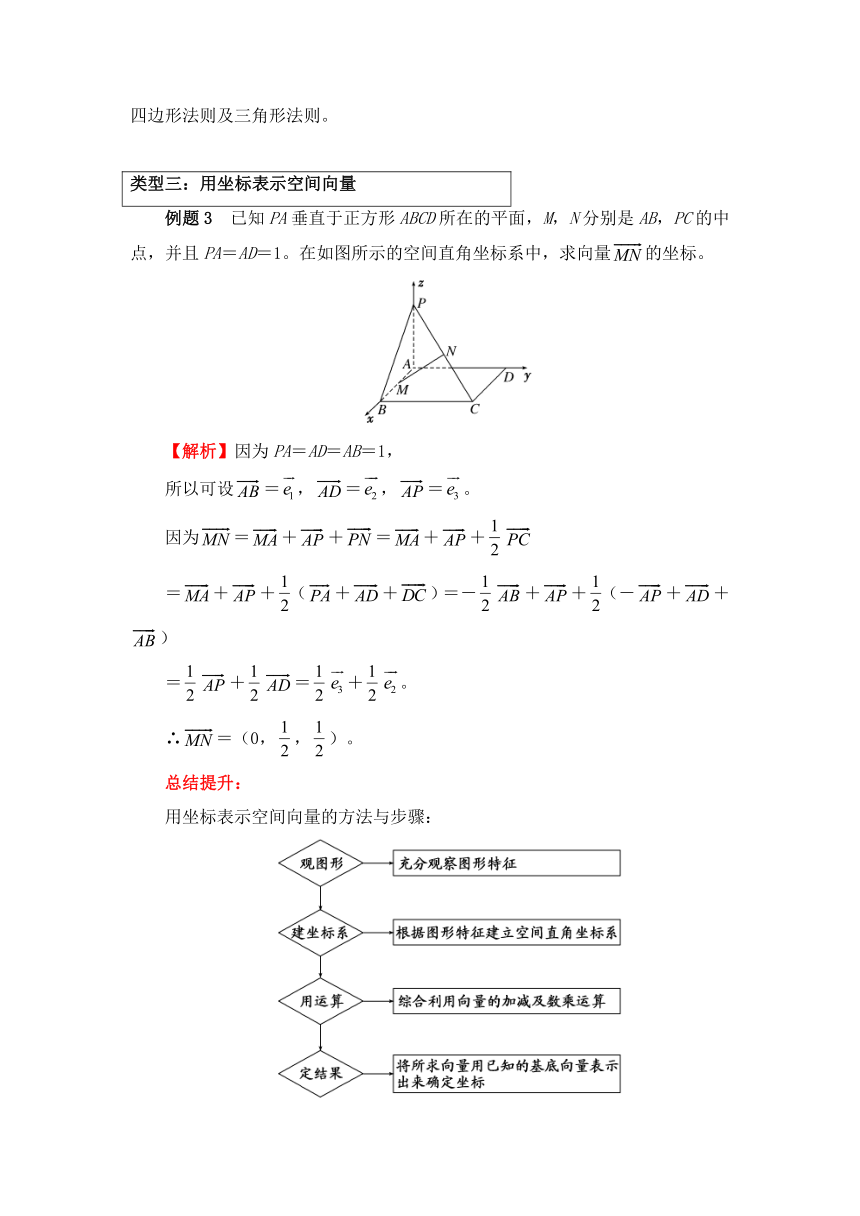
例题3 已知PA垂直于正方形ABCD所在的平面,M,N分别是AB,PC的中点,并且PA=AD=1。在如图所示的空间直角坐标系中,求向量false的坐标。
【解析】因为PA=AD=AB=1,
所以可设false=false,false=false,false=false。
因为false=false+false+false=false+false+falsefalse
=false+false+false(false+false+false)=-falsefalse+false+false(-false+false+false)
=falsefalse+falsefalse=falsefalse+falsefalse。
∴false=(0,false,false)。
总结提升:
用坐标表示空间向量的方法与步骤:
1. 三个向量不共面是三个向量构成空间一个基底的充要条件。
2. 用基底可表示空间任一向量,且表示方式是唯一的,解题时要注意三角形法则和平行四边形法则的应用;若基底false为单位正交基底,可由false得到false的坐标为(x,y,z)。
(答题时间:40分钟)
一、选择题
1. 在以下三个命题中,真命题的个数是( )
①三个非零向量false,false,false不能构成空间的一个基底,则false,false,false共面;
②若两个非零向量false,false与任何一个向量都不能构成空间的一个基底,则false,false共线;
③若false,false是两个不共线的向量,而false=λfalse+μfalse(λ,μ∈R且λμ≠0),则{false,false,false}构成空间的一个基底。
A. 0 B. 1
C. 2 D. 3
2. 已知{false,false,false}是空间的一个基底,则可以与向量false=false+false,false=false-false构成基底的向量是( )
A. false B. false
C. false+2false D. false+2false
3. 如图,长方体ABCD-A1B1C1D1中,AC与BD的交点为M。设false=false,false=false,false=false,则下列向量中与false相等的向量是( )
A. -falsefalse+falsefalse+false B. falsefalse+falsefalse+false
C. falsefalse-falsefalse+false D. -falsefalse-falsefalse+false
4. 已知点A在基底{false,false,false}下的坐标为(1,2,3),其中false=false,false=false,false=false,则点A在基底false下的坐标为( )
A. (7,3,12) B. (12,7,3)
C. (2,4,6) D. (12,3,7)
二、解答题
5. 如图所示,空间四边形OABC中,G是△ABC的重心,D为BC的中点,H为OD的中点。设false=false,false=false,false=false,试用向量false,false,false表示向量false。
6. 如图,在长方体ABCD-A1B1C1D1中,O为AC的中点。
(1)化简:false-falsefalse-falsefalse;
(2)设E是棱DD1上的点,且false=falsefalse,若false=xfalse+yfalse+zfalse,试求x,y,z的值。
1. 答案:C
解析:①正确。基底的向量必须不共面;②正确;③不对,false,false不共线,当false=λfalse+μfalse时false,false,false共面,故只有①②正确。
2. 答案:D
解析:能与false,false构成基底,则与false,false不共面。
∵false,false,false+2false=false。
∴A、B、C都不合题意。因为{false,false,false}为基底,
∴false+2false与false,false不共面,可构成基底。
3. 答案:A
解析:false=false+false+false
=-false+false+falsefalse
=-false+false+falsefalse+falsefalse
=-falsefalse+falsefalse+false。
4. 答案:A
解析:设O为坐标原点,则false=false+2false+3false=false+2false+3false=false,
∴点A在false下的坐标为(7,3,12)。
5. 解:false=false-false。
∵false=falsefalse=false(false+false)=false(false+false),
false=false+false=false+falsefalse=false+false(false-false)
=falsefalse+false×false(false+false)=falsefalse+false(false+false),
∴false=false(false+false)-falsefalse-false(false+false)=-falsefalse+falsefalse+falsefalse,
即false=-falsefalse+falsefalse+falsefalse。
6. 解:(1)∵false+false=false,
∴false-falsefalse-falsefalse=false-false(false+false)
=false-falsefalse=false-false=false。
(2)∵false=false+false=falsefalse+falsefalse
=falsefalse+false(false+false)
=falsefalse+falsefalse+falsefalse
=falsefalse-falsefalse-falsefalse,
∴x=false,y=-false,z=-false。
重点
1. 理解空间向量的基本定理及其意义;
2. 掌握空间向量的正交分解及其坐标表示。
难点
用不用的基底表示空间任一向量
考试要求
考试
题型 选择题、填空题、解答题
难度 中等
核心知识点一:空间向量基本定理
定理:如果三个向量false不共面,那么对任意一个空间向量false,存在唯一的有序实数组{x,y,z},使得false,其中false叫做空间的一个基底,false都叫做基向量。空间中任意三个不共面的向量都可以构成空间的一个基底。
核心知识点二:空间向量的正交分解
如果空间中的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用false表示。由空间向量基本定理可知,对空间中的任意向量false,均可以分解为三个向量false,使false。像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解。
注意:
(1)空间任意三个不共面的向量都可以作为空间向量的一个基底。
(2)false与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是false。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念。
核心知识点三:空间直角坐标系及向量坐标
1. 空间直角坐标系:在空间选定一点O和一个单位正交基底false。以点O为原点,分别以false的方向为正方向,以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴。这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,false都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分。
教材中所用的坐标系都是右手直角坐标系,其规则是:让右手拇指指向x轴正方向,食指指向y轴正方向,则中指指向z轴正方向。
2. 空间点的坐标:数轴Ox上点M用实数x表示,直角坐标平面上的点M用一对有序实数(x,y)表示,建立空间直角坐标系后,空间的点M可用有序实数组(x,y,z)表示。
在空间直角坐标系Oxyz中,false为坐标向量,对空间任意一点A,对应一个向量false,且点A的位置由向量false唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使false。
在单位正交基底false下与向量false对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中z叫做A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标。
3. 空间向量的坐标:在空间直角坐标系Oxyz中,给定向量false,作false。由空间向量基本定理,存在唯一的有序实数组(x,y,z),使false。有序实数组(x,y,z)叫做false在空间直角坐标系Oxyz中的坐标,上式可简记作false。
类型一:基底的判断
例题1 若false是空间的一个基底,试判断false能否作为该空间的一个基底。
【解析】假设false共面,则存在实数λ,μ使得falseλfalse+μfalse,∴false。
∵false为基底。∴false不共面。
∴false此方程组无解,∴false不共面。
∴false可以作为空间的一个基底。
总结提升:
判断给出的某一向量组能否作为基底,关键是要判断它们是否共面。如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断。
类型二:用基底表示向量
例题2 四棱锥P-OABC的底面为一矩形,PO⊥平面OABC。设false=false,false=false,false=false,E,F分别是PC和PB的中点,试用false,false,false表示false,false,false,false。
【解析】连接BO,则false=falsefalse=false(false+false)=false(false+false+false)=false(false-false-false)=-falsefalse-falsefalse+falsefalse。
false=false+false=-false+falsefalse=-false+false(false+false)=-false-falsefalse+falsefalse。
false=false+false=false+false+false(false+false)=-false+false+false(-false+false)=-false+falsefalse+falsefalse。
false=falsefalse=falsefalse=falsefalse。
总结提升:
用基底表示空间向量一般要用到向量的加法、减法、数乘的运算,包括平行四边形法则及三角形法则。
类型三:用坐标表示空间向量
例题3 已知PA垂直于正方形ABCD所在的平面,M,N分别是AB,PC的中点,并且PA=AD=1。在如图所示的空间直角坐标系中,求向量false的坐标。
【解析】因为PA=AD=AB=1,
所以可设false=false,false=false,false=false。
因为false=false+false+false=false+false+falsefalse
=false+false+false(false+false+false)=-falsefalse+false+false(-false+false+false)
=falsefalse+falsefalse=falsefalse+falsefalse。
∴false=(0,false,false)。
总结提升:
用坐标表示空间向量的方法与步骤:
1. 三个向量不共面是三个向量构成空间一个基底的充要条件。
2. 用基底可表示空间任一向量,且表示方式是唯一的,解题时要注意三角形法则和平行四边形法则的应用;若基底false为单位正交基底,可由false得到false的坐标为(x,y,z)。
(答题时间:40分钟)
一、选择题
1. 在以下三个命题中,真命题的个数是( )
①三个非零向量false,false,false不能构成空间的一个基底,则false,false,false共面;
②若两个非零向量false,false与任何一个向量都不能构成空间的一个基底,则false,false共线;
③若false,false是两个不共线的向量,而false=λfalse+μfalse(λ,μ∈R且λμ≠0),则{false,false,false}构成空间的一个基底。
A. 0 B. 1
C. 2 D. 3
2. 已知{false,false,false}是空间的一个基底,则可以与向量false=false+false,false=false-false构成基底的向量是( )
A. false B. false
C. false+2false D. false+2false
3. 如图,长方体ABCD-A1B1C1D1中,AC与BD的交点为M。设false=false,false=false,false=false,则下列向量中与false相等的向量是( )
A. -falsefalse+falsefalse+false B. falsefalse+falsefalse+false
C. falsefalse-falsefalse+false D. -falsefalse-falsefalse+false
4. 已知点A在基底{false,false,false}下的坐标为(1,2,3),其中false=false,false=false,false=false,则点A在基底false下的坐标为( )
A. (7,3,12) B. (12,7,3)
C. (2,4,6) D. (12,3,7)
二、解答题
5. 如图所示,空间四边形OABC中,G是△ABC的重心,D为BC的中点,H为OD的中点。设false=false,false=false,false=false,试用向量false,false,false表示向量false。
6. 如图,在长方体ABCD-A1B1C1D1中,O为AC的中点。
(1)化简:false-falsefalse-falsefalse;
(2)设E是棱DD1上的点,且false=falsefalse,若false=xfalse+yfalse+zfalse,试求x,y,z的值。
1. 答案:C
解析:①正确。基底的向量必须不共面;②正确;③不对,false,false不共线,当false=λfalse+μfalse时false,false,false共面,故只有①②正确。
2. 答案:D
解析:能与false,false构成基底,则与false,false不共面。
∵false,false,false+2false=false。
∴A、B、C都不合题意。因为{false,false,false}为基底,
∴false+2false与false,false不共面,可构成基底。
3. 答案:A
解析:false=false+false+false
=-false+false+falsefalse
=-false+false+falsefalse+falsefalse
=-falsefalse+falsefalse+false。
4. 答案:A
解析:设O为坐标原点,则false=false+2false+3false=false+2false+3false=false,
∴点A在false下的坐标为(7,3,12)。
5. 解:false=false-false。
∵false=falsefalse=false(false+false)=false(false+false),
false=false+false=false+falsefalse=false+false(false-false)
=falsefalse+false×false(false+false)=falsefalse+false(false+false),
∴false=false(false+false)-falsefalse-false(false+false)=-falsefalse+falsefalse+falsefalse,
即false=-falsefalse+falsefalse+falsefalse。
6. 解:(1)∵false+false=false,
∴false-falsefalse-falsefalse=false-false(false+false)
=false-falsefalse=false-false=false。
(2)∵false=false+false=falsefalse+falsefalse
=falsefalse+false(false+false)
=falsefalse+falsefalse+falsefalse
=falsefalse-falsefalse-falsefalse,
∴x=false,y=-false,z=-false。
