高中数学选择性必修(第一册)知识讲义 空间向量及线性运算典例精析-人教A版(2019)
文档属性
| 名称 | 高中数学选择性必修(第一册)知识讲义 空间向量及线性运算典例精析-人教A版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 417.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 09:52:45 | ||
图片预览



文档简介
空间向量及线性运算典例精析
重点
能运用空间向量的有关知识解决立体几何中的线性运算问题,证明有关向量共线问题,以及向量共面问题。
难点
对共线定理及共面定理的理解
考试要求
考试
题型 选择题、填空题、解答题
难度 中等
类型一:空间向量的线性运算
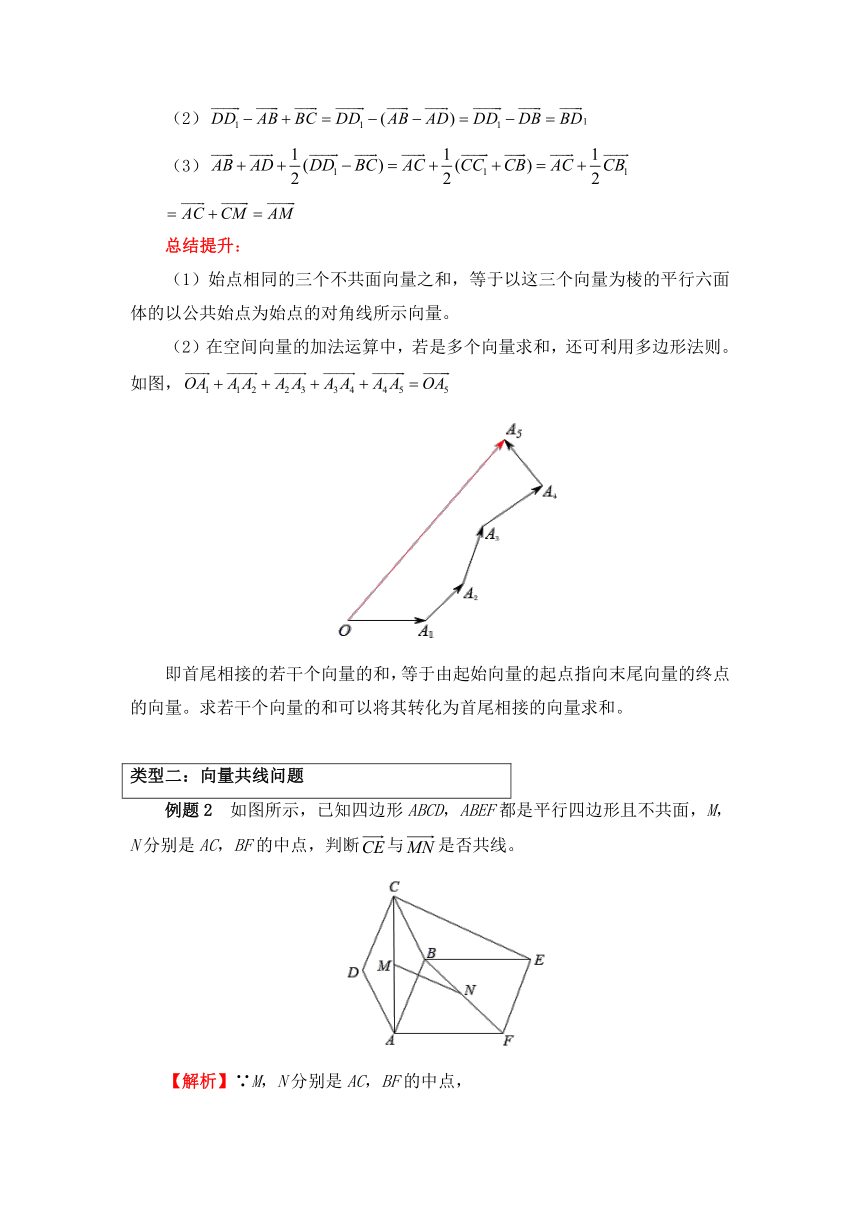
例题1 已知平行六面体ABCD-A1B1C1D1,M为B1C的中点,化简下列各向量表达式,并标出化简结果的向量。
(1)false;
(2)false;
(3)false。
【解析】(1)false
(2)false
(3)false
false
总结提升:
(1)始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量。
(2)在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则。如图,false
即首尾相接的若干个向量的和,等于由起始向量的起点指向末尾向量的终点的向量。求若干个向量的和可以将其转化为首尾相接的向量求和。
类型二:向量共线问题
例题2 如图所示,已知四边形ABCD,ABEF都是平行四边形且不共面,M,N分别是AC,BF的中点,判断false与false是否共线。
【解析】∵M,N分别是AC,BF的中点,
四边形ABCD,ABEF都是平行四边形,
∴false=false+false+false
=falsefalse+false+falsefalse
=false(false-false)+false+false(false+false)
=falsefalse+false+falsefalse
=false(false+false)
=falsefalse。
∴false∥false,即false与false共线。
总结提升:判定向量共线就是充分利用已知条件找到实数x,使false成立,同时要充分利用空间向量运算法则,结合具体的图形,化简得出false,从而得出false,即false与false共线。
类型三:向量共面问题
例题3 对于任意空间四边形ABCD,E,F分别是AB,CD的中点。
试证:false与false,false共面。
【解析】空间四边形ABCD中,E,F分别是AB,CD上的点,
则false=false+false+false,
false=false+false+false。①
又E,F分别是AB,CD的中点,故有false=-false,
false=-false。②
将②代入①中,两式相加得2 false=false+false。
所以false=falsefalse+falsefalse,即false与false,false共面。
总结提升:利用向量法证明向量共面问题,关键是熟练进行向量的表示,恰当应用向量共面的充要条件。解答本题实质上是证明存在实数x,y使向量false=xfalse+yfalse成立,也就是用空间向量的加、减法则及运算律,结合图形,用false,false表示false。
1. 化简空间向量式的常用思路
(1)统一成加法后利用空间多边形法则化简;
(2)利用向量的减法法则,即利用false化简;
(3)利用false把各个向量转化成与空间的某一点有关的向量化简。
2. 在几何体中用已知向量表示其他向量时的解答技巧
灵活运用空间向量的加法与减法法则,尽量走边路(即沿几何体的边选择途径),多个向量运算时,先观察分析“首尾相接”的向量使之结合,使用减法时,把握“共起点,方向指向被减向量”。
3. 利用共线向量定理可解决的主要问题及方法
(1)判定共线:判定两向量false是否共线,即判断是否存在实数λ,使false。
(2)求解参数:已知两非零向量共线,可求其中参数的值,即利用“若false,则false(λ∈R)”。
(3)判定或证明三点(如P,A,B)是否共线:
①考察是否存在实数λ,使false;
②考察对空间任意一点O,是否有false;
4. 利用共面向量定理需注意的问题
在利用false与false共面 false时,一定注意false不能共线。向量共面的充要条件是处理向量共面问题的主要依据。
(答题时间:30分钟)
一、选择题
1. 在正方体ABCD-A1B1C1D1中,false-false+false化简后的结果是( )
A. false B. false
C. false D. false
2. 在平行六面体ABCD-A′B′C′D′中,模与向量false的模相等的向量有( )
A. 7个 B. 3个
C. 5个 D. 6个
3. 如图所示,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点。若false=false,false=false,false=false,则下列向量中与false相等的向量是( )
A. -false+falsefalse+false B. falsefalse+falsefalse+false
C. falsefalse-falsefalse+false D. -falsefalse-falsefalse+false
4. 已知空间向量false,false,且false=false+2false,false=-5false+6false,false=7false-2false,则一定共线的三点是( )
A. A,B,D B. A,B,C
C. B,C,D D. A,C,D
5. 在四面体O-ABC中,false=false,false=false,false=false,D为BC的中点,E为AD的中点,则false=( )
A. false-false+false B. false-false+falsefalse
C. falsefalse+false+falsefalse D. falsefalse+falsefalse+falsefalse
二、解答题
6. 已知P是正方形ABCD所在平面外一点,P在平面ABCD上的射影恰好是正方形ABCD的中心O,Q是CD的中点,求下列各式中x,y的值:
(1)false=false+xfalse+yfalse;
(2)false=xfalse+yfalse+false。
7. 已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且false=falsefalse,false=falsefalse。
求证:四边形EFGH是梯形。
1. 答案:A
解析:由正方体的性质可得false-false+false=false-false+false=false+false=false。
2. 答案:A
解析:|false|=|false|=|false|=|false|=|false|=|false|=|false|=|false|。
3. 答案:A
解析:false=false+false=false+false(false-false)=false+falsefalse-falsefalse=-false+false+false。
4. 答案:A
解析:false=false+false=(-5false+6false)+(7false-2false)
=2false+4false=2false,∴A,B,D三点共线。
5. 答案:C
解析:false=false+false=false+falsefalse
=false+false×false(false+false)
=false+false(false-false+false-false)
=falsefalse+falsefalse+falsefalse
=false+false+false。
6. 解:(1)∵false=false-false
=false-false(false+false)
=false-falsefalse-falsefalse,
∴x=y=-false。
(2)∵false+false=2false,∴false=2false-false。
又∵false+false=2false,∴false=2false-false。
从而有false=2false-(2false-false)=2false-2false+false。
∴x=2,y=-2。
7. 证明:∵E,H分别是AB,AD的中点,
∴false=falsefalse,false=falsefalse,
false=false-false=falsefalse-falsefalse=false(false-false)
=falsefalse=false(false-false)=false(falsefalse-falsefalse)
=false(false-false)=falsefalse,
∴false∥false且|false|=false|false|≠|false|。
又点F不在false上,∴四边形EFGH是梯形。
重点
能运用空间向量的有关知识解决立体几何中的线性运算问题,证明有关向量共线问题,以及向量共面问题。
难点
对共线定理及共面定理的理解
考试要求
考试
题型 选择题、填空题、解答题
难度 中等
类型一:空间向量的线性运算
例题1 已知平行六面体ABCD-A1B1C1D1,M为B1C的中点,化简下列各向量表达式,并标出化简结果的向量。
(1)false;
(2)false;
(3)false。
【解析】(1)false
(2)false
(3)false
false
总结提升:
(1)始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量。
(2)在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则。如图,false
即首尾相接的若干个向量的和,等于由起始向量的起点指向末尾向量的终点的向量。求若干个向量的和可以将其转化为首尾相接的向量求和。
类型二:向量共线问题
例题2 如图所示,已知四边形ABCD,ABEF都是平行四边形且不共面,M,N分别是AC,BF的中点,判断false与false是否共线。
【解析】∵M,N分别是AC,BF的中点,
四边形ABCD,ABEF都是平行四边形,
∴false=false+false+false
=falsefalse+false+falsefalse
=false(false-false)+false+false(false+false)
=falsefalse+false+falsefalse
=false(false+false)
=falsefalse。
∴false∥false,即false与false共线。
总结提升:判定向量共线就是充分利用已知条件找到实数x,使false成立,同时要充分利用空间向量运算法则,结合具体的图形,化简得出false,从而得出false,即false与false共线。
类型三:向量共面问题
例题3 对于任意空间四边形ABCD,E,F分别是AB,CD的中点。
试证:false与false,false共面。
【解析】空间四边形ABCD中,E,F分别是AB,CD上的点,
则false=false+false+false,
false=false+false+false。①
又E,F分别是AB,CD的中点,故有false=-false,
false=-false。②
将②代入①中,两式相加得2 false=false+false。
所以false=falsefalse+falsefalse,即false与false,false共面。
总结提升:利用向量法证明向量共面问题,关键是熟练进行向量的表示,恰当应用向量共面的充要条件。解答本题实质上是证明存在实数x,y使向量false=xfalse+yfalse成立,也就是用空间向量的加、减法则及运算律,结合图形,用false,false表示false。
1. 化简空间向量式的常用思路
(1)统一成加法后利用空间多边形法则化简;
(2)利用向量的减法法则,即利用false化简;
(3)利用false把各个向量转化成与空间的某一点有关的向量化简。
2. 在几何体中用已知向量表示其他向量时的解答技巧
灵活运用空间向量的加法与减法法则,尽量走边路(即沿几何体的边选择途径),多个向量运算时,先观察分析“首尾相接”的向量使之结合,使用减法时,把握“共起点,方向指向被减向量”。
3. 利用共线向量定理可解决的主要问题及方法
(1)判定共线:判定两向量false是否共线,即判断是否存在实数λ,使false。
(2)求解参数:已知两非零向量共线,可求其中参数的值,即利用“若false,则false(λ∈R)”。
(3)判定或证明三点(如P,A,B)是否共线:
①考察是否存在实数λ,使false;
②考察对空间任意一点O,是否有false;
4. 利用共面向量定理需注意的问题
在利用false与false共面 false时,一定注意false不能共线。向量共面的充要条件是处理向量共面问题的主要依据。
(答题时间:30分钟)
一、选择题
1. 在正方体ABCD-A1B1C1D1中,false-false+false化简后的结果是( )
A. false B. false
C. false D. false
2. 在平行六面体ABCD-A′B′C′D′中,模与向量false的模相等的向量有( )
A. 7个 B. 3个
C. 5个 D. 6个
3. 如图所示,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点。若false=false,false=false,false=false,则下列向量中与false相等的向量是( )
A. -false+falsefalse+false B. falsefalse+falsefalse+false
C. falsefalse-falsefalse+false D. -falsefalse-falsefalse+false
4. 已知空间向量false,false,且false=false+2false,false=-5false+6false,false=7false-2false,则一定共线的三点是( )
A. A,B,D B. A,B,C
C. B,C,D D. A,C,D
5. 在四面体O-ABC中,false=false,false=false,false=false,D为BC的中点,E为AD的中点,则false=( )
A. false-false+false B. false-false+falsefalse
C. falsefalse+false+falsefalse D. falsefalse+falsefalse+falsefalse
二、解答题
6. 已知P是正方形ABCD所在平面外一点,P在平面ABCD上的射影恰好是正方形ABCD的中心O,Q是CD的中点,求下列各式中x,y的值:
(1)false=false+xfalse+yfalse;
(2)false=xfalse+yfalse+false。
7. 已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且false=falsefalse,false=falsefalse。
求证:四边形EFGH是梯形。
1. 答案:A
解析:由正方体的性质可得false-false+false=false-false+false=false+false=false。
2. 答案:A
解析:|false|=|false|=|false|=|false|=|false|=|false|=|false|=|false|。
3. 答案:A
解析:false=false+false=false+false(false-false)=false+falsefalse-falsefalse=-false+false+false。
4. 答案:A
解析:false=false+false=(-5false+6false)+(7false-2false)
=2false+4false=2false,∴A,B,D三点共线。
5. 答案:C
解析:false=false+false=false+falsefalse
=false+false×false(false+false)
=false+false(false-false+false-false)
=falsefalse+falsefalse+falsefalse
=false+false+false。
6. 解:(1)∵false=false-false
=false-false(false+false)
=false-falsefalse-falsefalse,
∴x=y=-false。
(2)∵false+false=2false,∴false=2false-false。
又∵false+false=2false,∴false=2false-false。
从而有false=2false-(2false-false)=2false-2false+false。
∴x=2,y=-2。
7. 证明:∵E,H分别是AB,AD的中点,
∴false=falsefalse,false=falsefalse,
false=false-false=falsefalse-falsefalse=false(false-false)
=falsefalse=false(false-false)=false(falsefalse-falsefalse)
=false(false-false)=falsefalse,
∴false∥false且|false|=false|false|≠|false|。
又点F不在false上,∴四边形EFGH是梯形。
