数学八年级上册第1章 全等三角形同步练习-青岛版(Word版含答案)
文档属性
| 名称 | 数学八年级上册第1章 全等三角形同步练习-青岛版(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 14:21:14 | ||
图片预览


文档简介
第1章 全等三角形同步练习
(答题时间:60分钟)
全等三角形的有关概念同步练习
一、选择题
1. 已知△ABC≌△DEF,∠A=50°,∠B=75°,则∠F的大小为( )
A. 50° B. 55° C. 65° D. 75°
*2. 如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A. 5 B. 4 C. 3 D. 2
**3. 如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF。如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为( )
A. 24cm? B. 25cm? C. 26cm? D. 27cm?
二、填空题
*4. 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于________。
*5. 如图,D是AB边上的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上的F处,若∠B=50°,则∠BDF=________。
*6. 如图,D在AB上,AC,DF交于E,AB∥FC,DE=EF,AB=15,CF=8,则BD= 。
三、解答题
7. 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF。能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明。
供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE。
*8. 支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?
全等三角形的判定方法同步练习
一、选择题
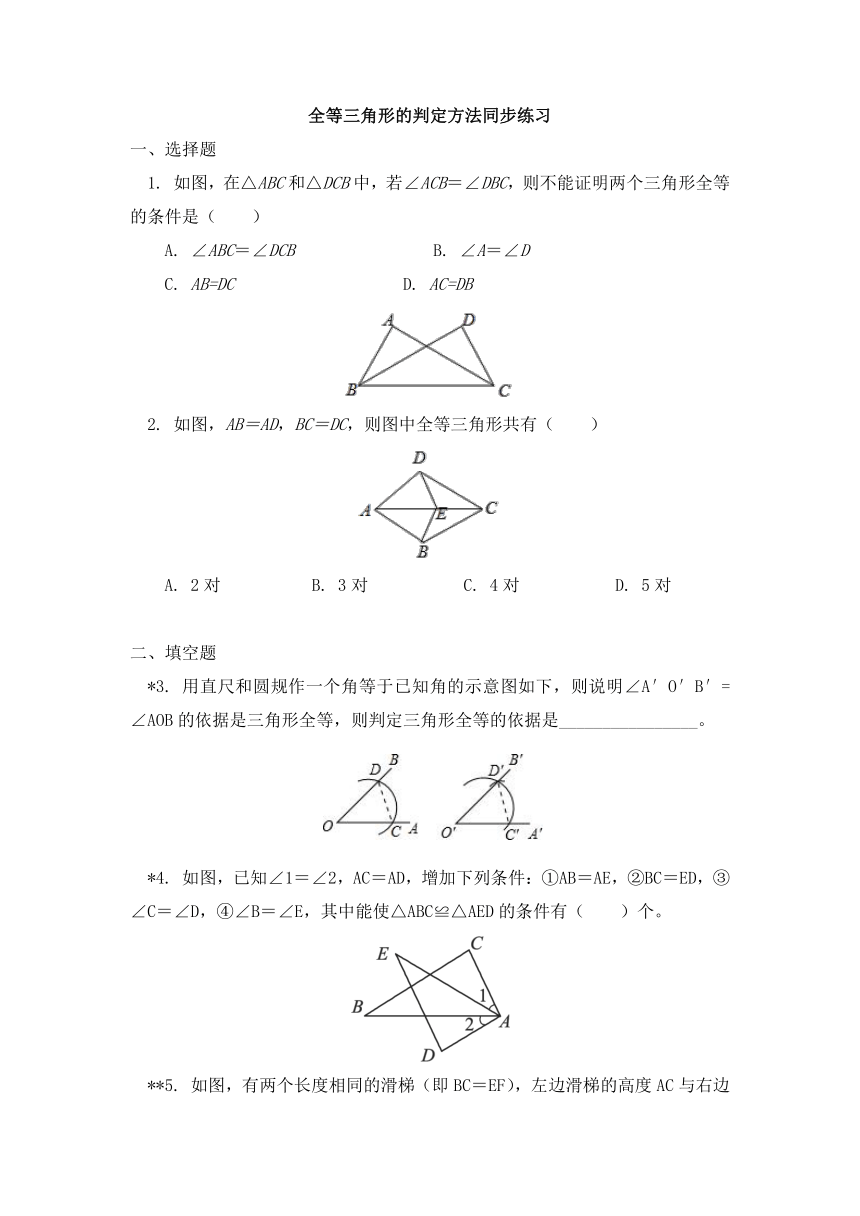
1. 如图,在△ABC和△DCB中,若∠ACB=∠DBC,则不能证明两个三角形全等的条件是( )
A. ∠ABC=∠DCB B. ∠A=∠D
C. AB=DC D. AC=DB
2. 如图,AB=AD,BC=DC,则图中全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
二、填空题
*3. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是三角形全等,则判定三角形全等的依据是________________。
*4. 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有( )个。
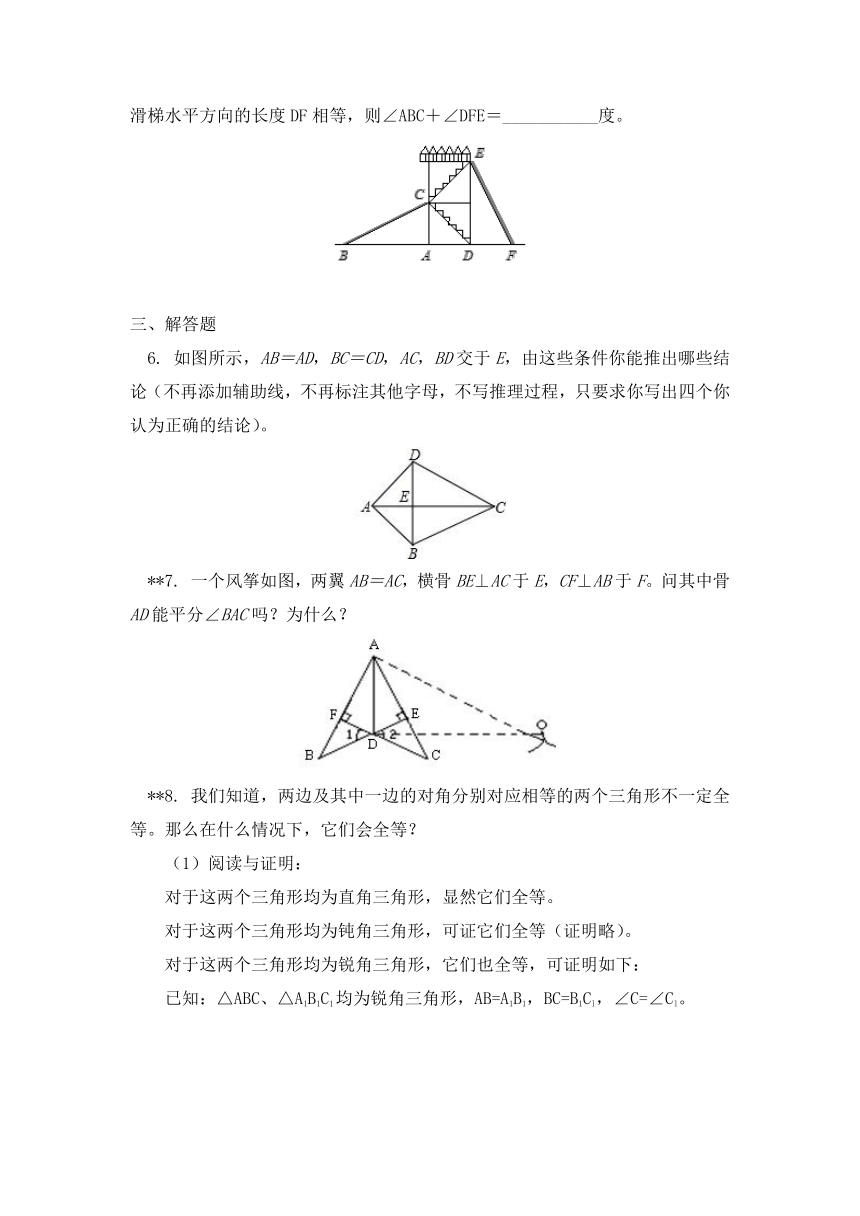
**5. 如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度。
三、解答题
6. 如图所示,AB=AD,BC=CD,AC,BD交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注其他字母,不写推理过程,只要求你写出四个你认为正确的结论)。
**7. 一个风筝如图,两翼AB=AC,横骨BE⊥AC于E,CF⊥AB于F。问其中骨AD能平分∠BAC吗?为什么?
**8. 我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等。那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等。
对于这两个三角形均为钝角三角形,可证它们全等(证明略)。
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl。
求证:△ABC≌△A1B1C1。
(请你将下列证明过程补充完整。)
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1。
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1。
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论。
**9. 两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC,
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE。
第1章 全等三角形同步练习参考答案
全等三角形的有关概念同步练习参考答案
1. B 解析:∠F与∠C是全等三角形的对应角,所以∠F=∠C=180°-∠A-∠B=180°-50°-75°=55°。
2. A 解析:由△ABC≌△DEF,可得AB=DE,则DE=AB=BE+AE=5。
3. C 解析:三角形ABC和三角形DEF全等,它们的面积相等,三角形HEC是两三角形重合的部分,两个三角形都减去重合的部分,剩下的部分是相等的,也就是HDFC与ABEH面积是相等的。那么只要求出ABHE的面积就可知阴影部分的面积了,即:(5+8)×4/2=26。
4. 60° 解析:因为OA=OB,OD=OC,∠O=∠O,所以△OAD≌△OBC,得到∠C=∠D=35°。由三角形的内外角关系可得,∠EAC=∠O+∠D=50°+35°=85°,所以∠AEC=180°-∠EAC-∠C=60°
5. 80° 解析:由折叠得△ADE≌△FDE,所以AD=DF,又AD=BD,∴BD=DF,又∠B=50°,∴∠BDF=180°-50°×2=80°。
6. 7 解析:由题易得△ADE≌△CEF,所以BD=AB-AD=AB-CF=15-8=7
7. 解:由上面两条件不能证明AB//ED。
有两种添加方法。
第一种:FB=CE,AC=DF添加 ①AB=ED
证明:因为FB=CE,所以BC=EF,又AC=DF,AB=ED,所以△ABC≌△DEF
所以∠ABC=∠DEF 所以AB//ED
第二种:FB=CE,AC=DF添加 ③∠ACB=∠DFE
证明:因为FB=CE,所以BC=EF,又∠ACB=∠DFE AC=EF,所以△ABC≌△DEF
所以∠ABC=∠DEF 所以AB//ED
8. AD=AE 解:∵AM=AN ∠MAC=∠NAB AB=AC ∴△MAC≌△NAB(SAS)∴∠C=∠B
∵∠DAB=∠EAC∴∠DAB+∠BAC=∠EAC+∠BAC∴∠DAC=∠EAB ∵∠C=∠B,AB=AC
△DAC≌△EAB(ASA)∴AD=AE
全等三角形的判定方法同步练习参考答案
1. C 解析:SSA不能判定三角形全等。
2. B 解析:△ADE≌△ABE , △ADC≌△ABC , △DEC≌△BEC
3. SSS 解析:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',则∠COD≌∠C'O'D',即∠A'O'B'=∠AOB(全等三角形的对应角相等)。
4. 3 解析:增加①AB=AE,则△ABC≌△AED(SAS);增加③∠C=∠D,则△ABC≌△AED(ASA);增加④∠B=∠E,则△ABC≌△AED(AAS)。
5. 90 解析:∵∠CAB=∠EDF=90°,∴△ABC与△DEF为直角三角形,又∵EF=BC,AC=DF,△ABC≌△DEF,∴∠ABC+∠DFE=∠ABC+∠ACB=90°
6. (1)△ADC≌△ABC;(2)AC平分∠DCB;(3)AC平分∠DAB;(4)DE=EB;(5)DB⊥AC;
7. AD能平分∠BAC;解:由∠1=∠2,得∠B=∠C,又AB=AC,故△ABE≌△ACF,从而AE=AF,又AD=AD,故Rt△ADF≌Rt△ADE,得∠FAD=∠EAD
8.(1)证明:分别过点B,B1作BD⊥CA于D
B1D1⊥C1A1于D1
则∠BDC=∠B1D1C1=90°
∵BC=B1C1,∠C=∠C1
∴△BCD≌△B1C1D1
∴BD=B1D1 又∵AB=A1B1 ∠BDC=∠B1D1C1=90° ∴△ABD≌△A1B1D1 ∴∠A=∠A1 又∵AB=A1B1,∠C=∠C1 ∴△ABC≌△A1B1C1
(2)归纳与叙述:由(1)可得到一个正确结论,两边及其中一边的对角分别对应相等的两个同类三角形(同为锐角、直角、钝角三角形)一定全等
9. △BAE≌△CAD 解:①∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中
AB=AC ∠BAE=∠DAC AE=AD
∴△BAE≌△CAD(SAS)
②由①得△BAE≌△CAD
∴∠DCA=∠B=45°
∵∠BCA=45°
∴∠BCD=∠BCA+∠DCA=90°
∴DC⊥BE
(答题时间:60分钟)
全等三角形的有关概念同步练习
一、选择题
1. 已知△ABC≌△DEF,∠A=50°,∠B=75°,则∠F的大小为( )
A. 50° B. 55° C. 65° D. 75°
*2. 如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A. 5 B. 4 C. 3 D. 2
**3. 如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF。如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为( )
A. 24cm? B. 25cm? C. 26cm? D. 27cm?
二、填空题
*4. 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于________。
*5. 如图,D是AB边上的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上的F处,若∠B=50°,则∠BDF=________。
*6. 如图,D在AB上,AC,DF交于E,AB∥FC,DE=EF,AB=15,CF=8,则BD= 。
三、解答题
7. 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF。能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明。
供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE。
*8. 支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?
全等三角形的判定方法同步练习
一、选择题
1. 如图,在△ABC和△DCB中,若∠ACB=∠DBC,则不能证明两个三角形全等的条件是( )
A. ∠ABC=∠DCB B. ∠A=∠D
C. AB=DC D. AC=DB
2. 如图,AB=AD,BC=DC,则图中全等三角形共有( )
A. 2对 B. 3对 C. 4对 D. 5对
二、填空题
*3. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是三角形全等,则判定三角形全等的依据是________________。
*4. 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有( )个。
**5. 如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度。
三、解答题
6. 如图所示,AB=AD,BC=CD,AC,BD交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注其他字母,不写推理过程,只要求你写出四个你认为正确的结论)。
**7. 一个风筝如图,两翼AB=AC,横骨BE⊥AC于E,CF⊥AB于F。问其中骨AD能平分∠BAC吗?为什么?
**8. 我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等。那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等。
对于这两个三角形均为钝角三角形,可证它们全等(证明略)。
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl。
求证:△ABC≌△A1B1C1。
(请你将下列证明过程补充完整。)
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1。
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1。
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论。
**9. 两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC,
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE。
第1章 全等三角形同步练习参考答案
全等三角形的有关概念同步练习参考答案
1. B 解析:∠F与∠C是全等三角形的对应角,所以∠F=∠C=180°-∠A-∠B=180°-50°-75°=55°。
2. A 解析:由△ABC≌△DEF,可得AB=DE,则DE=AB=BE+AE=5。
3. C 解析:三角形ABC和三角形DEF全等,它们的面积相等,三角形HEC是两三角形重合的部分,两个三角形都减去重合的部分,剩下的部分是相等的,也就是HDFC与ABEH面积是相等的。那么只要求出ABHE的面积就可知阴影部分的面积了,即:(5+8)×4/2=26。
4. 60° 解析:因为OA=OB,OD=OC,∠O=∠O,所以△OAD≌△OBC,得到∠C=∠D=35°。由三角形的内外角关系可得,∠EAC=∠O+∠D=50°+35°=85°,所以∠AEC=180°-∠EAC-∠C=60°
5. 80° 解析:由折叠得△ADE≌△FDE,所以AD=DF,又AD=BD,∴BD=DF,又∠B=50°,∴∠BDF=180°-50°×2=80°。
6. 7 解析:由题易得△ADE≌△CEF,所以BD=AB-AD=AB-CF=15-8=7
7. 解:由上面两条件不能证明AB//ED。
有两种添加方法。
第一种:FB=CE,AC=DF添加 ①AB=ED
证明:因为FB=CE,所以BC=EF,又AC=DF,AB=ED,所以△ABC≌△DEF
所以∠ABC=∠DEF 所以AB//ED
第二种:FB=CE,AC=DF添加 ③∠ACB=∠DFE
证明:因为FB=CE,所以BC=EF,又∠ACB=∠DFE AC=EF,所以△ABC≌△DEF
所以∠ABC=∠DEF 所以AB//ED
8. AD=AE 解:∵AM=AN ∠MAC=∠NAB AB=AC ∴△MAC≌△NAB(SAS)∴∠C=∠B
∵∠DAB=∠EAC∴∠DAB+∠BAC=∠EAC+∠BAC∴∠DAC=∠EAB ∵∠C=∠B,AB=AC
△DAC≌△EAB(ASA)∴AD=AE
全等三角形的判定方法同步练习参考答案
1. C 解析:SSA不能判定三角形全等。
2. B 解析:△ADE≌△ABE , △ADC≌△ABC , △DEC≌△BEC
3. SSS 解析:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',则∠COD≌∠C'O'D',即∠A'O'B'=∠AOB(全等三角形的对应角相等)。
4. 3 解析:增加①AB=AE,则△ABC≌△AED(SAS);增加③∠C=∠D,则△ABC≌△AED(ASA);增加④∠B=∠E,则△ABC≌△AED(AAS)。
5. 90 解析:∵∠CAB=∠EDF=90°,∴△ABC与△DEF为直角三角形,又∵EF=BC,AC=DF,△ABC≌△DEF,∴∠ABC+∠DFE=∠ABC+∠ACB=90°
6. (1)△ADC≌△ABC;(2)AC平分∠DCB;(3)AC平分∠DAB;(4)DE=EB;(5)DB⊥AC;
7. AD能平分∠BAC;解:由∠1=∠2,得∠B=∠C,又AB=AC,故△ABE≌△ACF,从而AE=AF,又AD=AD,故Rt△ADF≌Rt△ADE,得∠FAD=∠EAD
8.(1)证明:分别过点B,B1作BD⊥CA于D
B1D1⊥C1A1于D1
则∠BDC=∠B1D1C1=90°
∵BC=B1C1,∠C=∠C1
∴△BCD≌△B1C1D1
∴BD=B1D1 又∵AB=A1B1 ∠BDC=∠B1D1C1=90° ∴△ABD≌△A1B1D1 ∴∠A=∠A1 又∵AB=A1B1,∠C=∠C1 ∴△ABC≌△A1B1C1
(2)归纳与叙述:由(1)可得到一个正确结论,两边及其中一边的对角分别对应相等的两个同类三角形(同为锐角、直角、钝角三角形)一定全等
9. △BAE≌△CAD 解:①∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中
AB=AC ∠BAE=∠DAC AE=AD
∴△BAE≌△CAD(SAS)
②由①得△BAE≌△CAD
∴∠DCA=∠B=45°
∵∠BCA=45°
∴∠BCD=∠BCA+∠DCA=90°
∴DC⊥BE
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
