数学八年级上册1.1-1.2探索勾股定理;一定是直角三角形吗同步练习(Word版含答案)
文档属性
| 名称 | 数学八年级上册1.1-1.2探索勾股定理;一定是直角三角形吗同步练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 14:17:50 | ||
图片预览


文档简介
初二数学北师大版(2012教材)第一章 1.1-1.2 探索勾股定理;一定是直角三角形-同步练习
(答题时间:60分钟)
微课程:探索勾股定理同步练习
一、选择题
1. 如果直角三角形的三条边为2,4,a,那么a2的取值可以有( )
A. 0个 B. 1个 C. 2个 D. 3个
2. 一棵树在离地5米处断裂,树顶落在离树根12米处,问树断之前有多高( )米
A. 17 B. 17.5 C. 18 D. 20
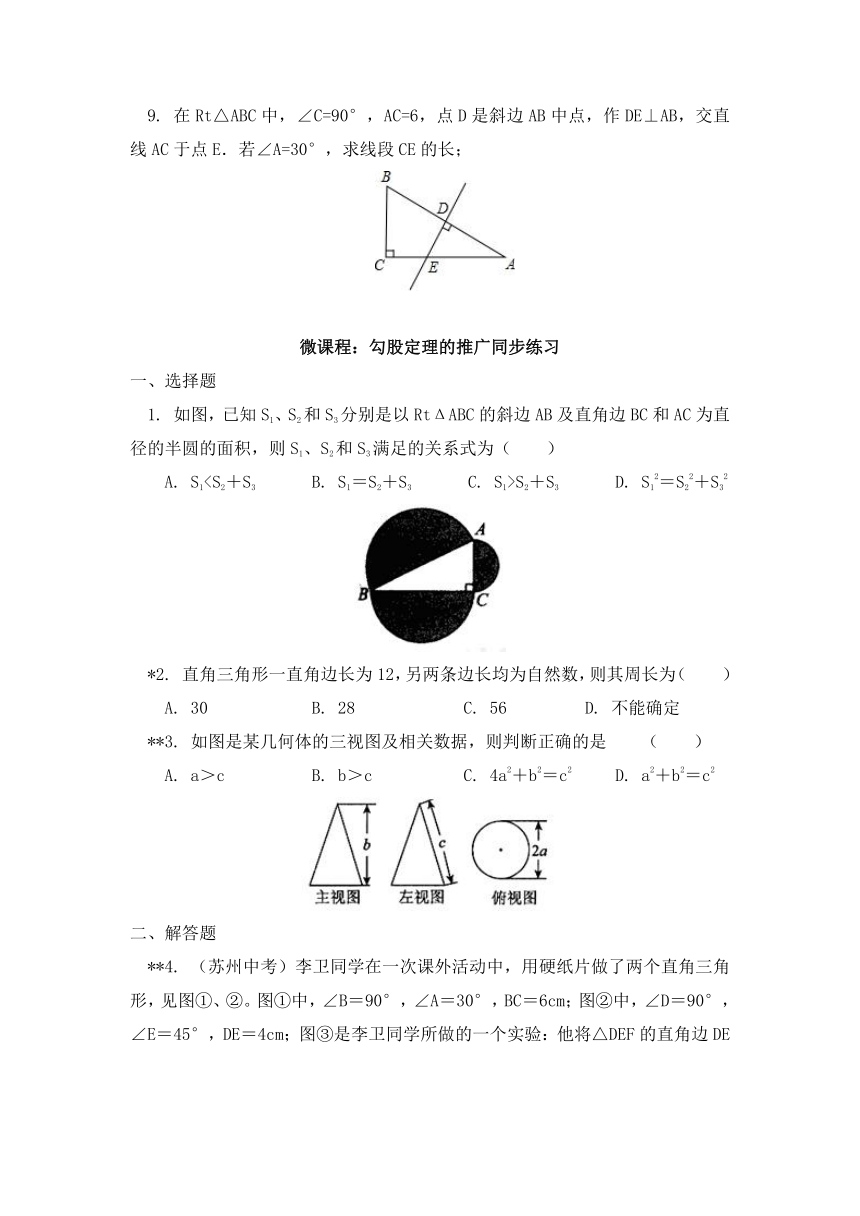
*3. (本溪中考)如图,在直角△ABC中,,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为( )
A. 16 B. 15 C. 14 D. 13
二、填空题
4. △ABC中,∠C=90o,AB=3,则AB2+BC2+AC2=_______。
*5. 如图,两个正方形的面积分别是25cm2和169 cm2,则直角三角形中边BC=____cm。
*6. 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=6,BC=5,将四个这样的直角三角形中边长为6的直角边向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是_________。
三、解答题
**7. (温州中考)勾股定理有着悠久的历史,它曾引起很多人的兴趣。l955年希腊发行了二枚以勾股图为背景的邮票。所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理。在下图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4。作
△PQR使得∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边_PQ上,则我们可发现△CGF≌△CAB,那么QH2+RD2的长等于多少?
8. 如图在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则BC的值。
9. 在Rt△ABC中,∠C=90°,AC=6,点D是斜边AB中点,作DE⊥AB,交直线AC于点E.若∠A=30°,求线段CE的长;
微课程:勾股定理的推广同步练习
一、选择题
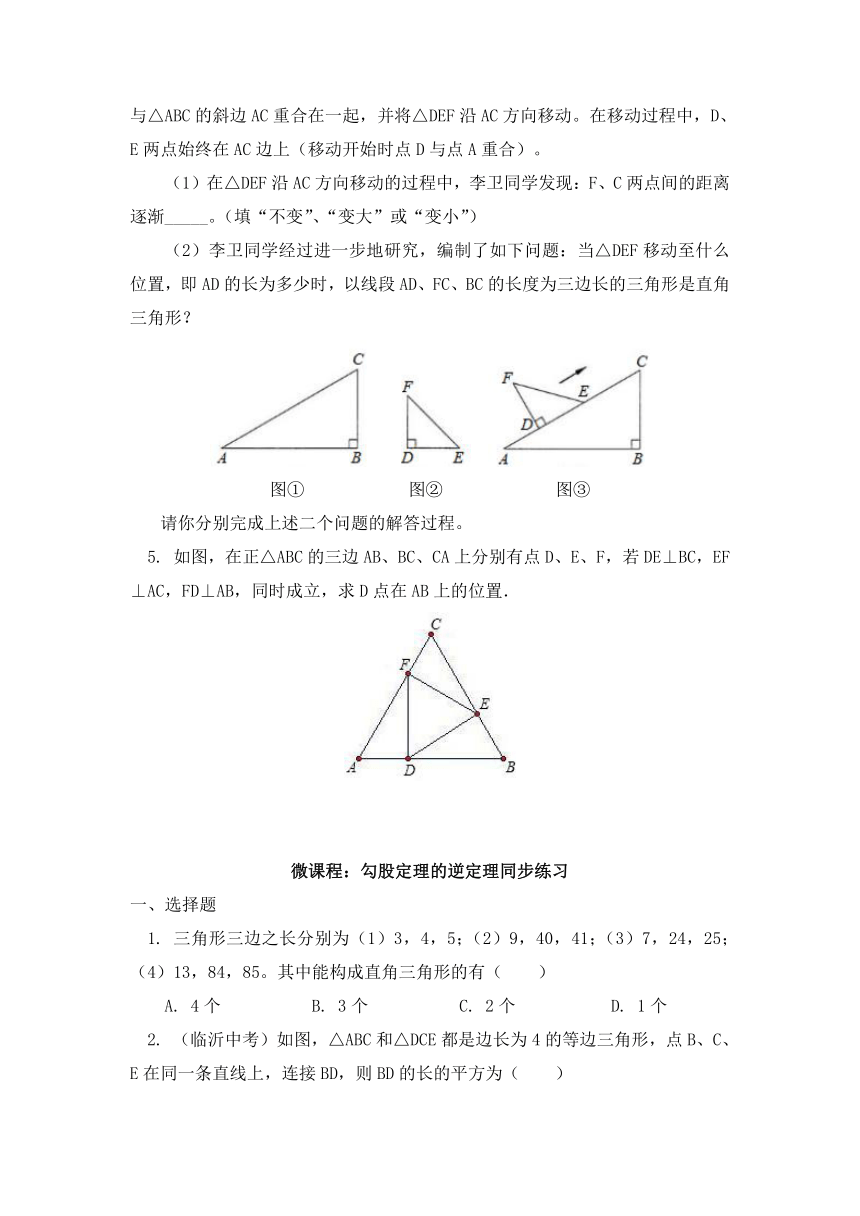
1. 如图,已知S1、S2和S3分别是以RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、S2和S3满足的关系式为( )
A. S1S2+S3 D. S12=S22+S32
*2. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( )
A. 30 B. 28 C. 56 D. 不能确定
**3. 如图是某几何体的三视图及相关数据,则判断正确的是 ( )
A. a>c B. b>c C. 4a2+b2=c2 D. a2+b2=c2
二、解答题
**4. (苏州中考)李卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②。图①中,∠B=90°,∠A=30°,BC=6cm;图②中,∠D=90°,∠E=45°,DE=4cm;图③是李卫同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动。在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合)。
(1)在△DEF沿AC方向移动的过程中,李卫同学发现:F、C两点间的距离逐渐_____。(填“不变”、“变大”或“变小”)
(2)李卫同学经过进一步地研究,编制了如下问题:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
图① 图② 图③
请你分别完成上述二个问题的解答过程。
5. 如图,在正△ABC的三边AB、BC、CA上分别有点D、E、F,若DE⊥BC,EF⊥AC,FD⊥AB,同时成立,求D点在AB上的位置.
微课程:勾股定理的逆定理同步练习
一、选择题
1. 三角形三边之长分别为(1)3,4,5;(2)9,40,41;(3)7,24,25;(4)13,84,85。其中能构成直角三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
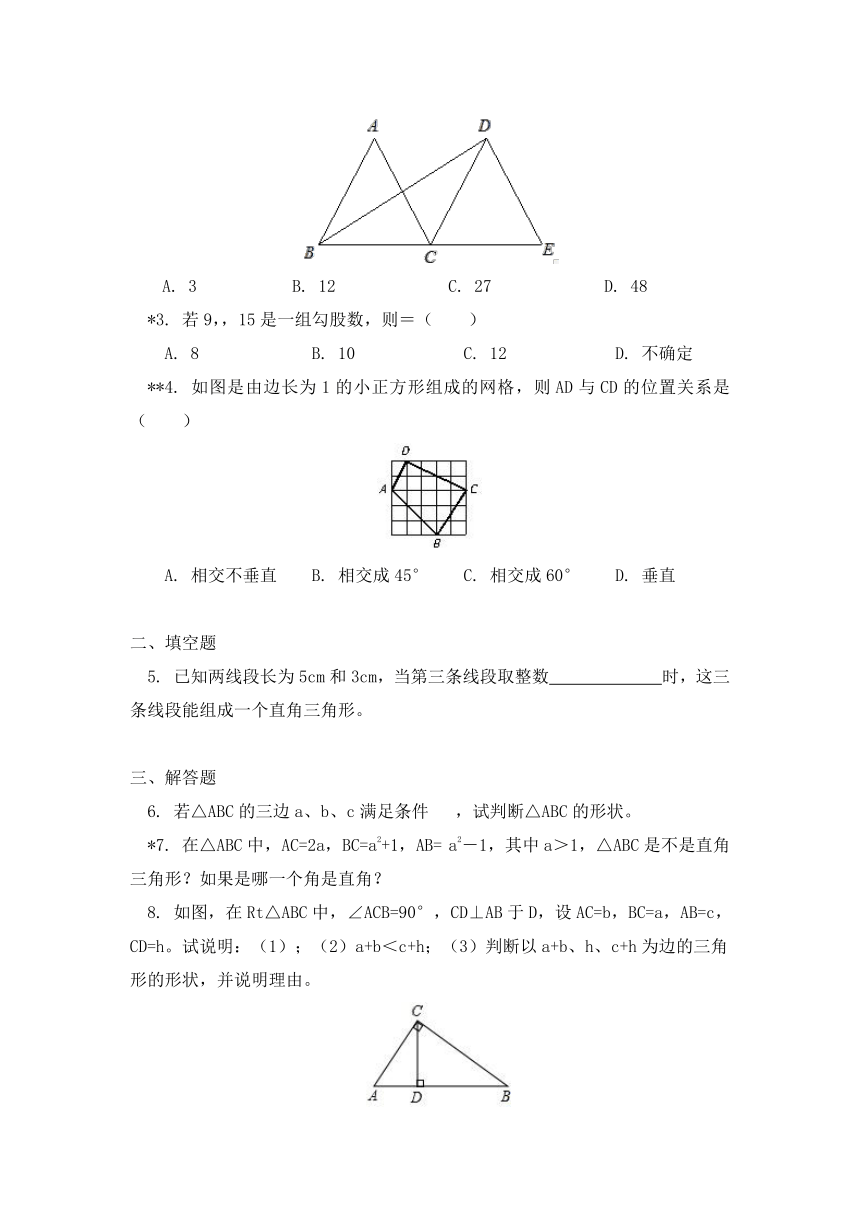
2. (临沂中考)如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长的平方为( )
A. 3 B. 12 C. 27 D. 48
*3. 若9,,15是一组勾股数,则=( )
A. 8 B. 10 C. 12 D. 不确定
**4. 如图是由边长为1的小正方形组成的网格,则AD与CD的位置关系是( )
A. 相交不垂直 B. 相交成45° C. 相交成60° D. 垂直
二、填空题
5. 已知两线段长为5cm和3cm,当第三条线段取整数 时,这三条线段能组成一个直角三角形。
三、解答题
6. 若△ABC的三边a、b、c满足条件 ,试判断△ABC的形状。
*7. 在△ABC中,AC=2a,BC=a2+1,AB= a2-1,其中a>1,△ABC是不是直角三角形?如果是哪一个角是直角?
8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h。试说明:(1);(2)a+b<c+h;(3)判断以a+b、h、c+h为边的三角形的形状,并说明理由。
初二数学北师大版(2012教材)第一章 1.1-1.2 探索勾股定理;一定是直角三角形?同步练习参考答案
微课程:探索勾股定理同步练习参考答案
1. C 解析:因为该三角形为直角三角形,所以满足a2+b2 =c2。在三边中,a有可能为直角边,也有可能为斜边,所以应选C。
2. C 解析:在Rt△ABC中标出已知条件,从而由勾股定理求得AB的长,再加上5米可知树高为18米。
*3. A 解析:直角△ABC中,,AB=8,AC=6,所以BC=10,因为DE是AB边的垂直平分线,所以AE=BE;=AC+CE+EA= AC+CE+BE=AC+BC=16。
4. 18 解析:根据勾股定理得BC2+AC2=AB2,所以AB2+BC2+AC2=(BC2+AC2)+AB2=AB2+AB2=2AB 2 =2×3 2=18。
*5. 12 解析:因为∠ABC=90°,所以由勾股定理得AB 2+BC 2=AC 2,即有25+BC 2=169,BC=12。
*6. 76 解析:利用勾股定理可以直接求解。
**7. 16 解析:题中仅知AB长,估计要求的要想方法联系它,要求的是平方和形式,则若它们在同一个三角形中,就有可能用勾股定理,但不在一起,则想方法把它们(或它们的相等线段)放在同一三角形中。过点A作AM⊥QH于点M,则可得△HMA≌△ACB,得∠QHG=60°,RD=AM=BC;△GCF≌△ACB,得∠QGH=60°,则△QHG是等边三角形,得QH=HG=AC,则QH2+RD2=AC2+BC2=AB2=16。
8. 解:∵在△ADE和△ADC中,
∴△ADE≌△ADC(AAS),
∴CD=DE,∵BD=2CD,
∴BC=BD+CD=3DE=9.
∴BC=9.
答:线段BC的长为9.
9. 解:连接BE,点D是斜边AB中点且DE⊥AB,
∵∠A=30°,∴∠ABC=90°-30°=60°,
又∵DE垂直平分AB,
∴∠ABE=∠BAE=30°,∠CBE=∠ABC-∠ABE=30°,
又∵∠C=90°,∴CE=·BE=·AE,
∵AC=6,∴BE=AE=4,CE=BE=×4=2
答:线段CE的长为2。
微课程:勾股定理的推广同步练习参考答案
1. B 解析:三个半圆的面积为π(边长之半)2=π(边长)2,而两个小的(边长)2之和=(大的边长)2,则两个小的面积之和等于大的面积。
*2. D 解析:例如9,12,15;12,16,20都满足条件。
**3. D 解析:弄清楚三视图之间的关系,本题只要知道主视图和左视图中三角形的底是俯视图中圆的直径,再利用勾股定理可解。
**4. 解析:(1)变小。
(2)解:设AD=x,在Rt△FDC中,FC2=DC2+FD2=(12-x)2+16
(Ⅰ)当FC为斜边时,
由AD2+BC2=FC2得,x2+62=(12-x)2+16,x=
(Ⅱ)当AD为斜边时,
由AD2=FC2+BC2得,x2=(12-x)2+16+62,x=>8(不符合题意,舍去)。
(Ⅲ)当BC为斜边时,
∵FC>CD∴FC+AD>12
∴FC、AD中至少有一条线段的长度大于6,
∴BC不能为斜边,
∴由(Ⅰ)、(Ⅱ)、(Ⅲ)得,当时,经线段AD、FC、BC的长度为三边长的三角形是直角三角形。
5. 解:∵DE⊥BC,
∴∠BDE=90°-∠B=30°,BD=2BE,
∴∠EDF=60°,同理∠DEF=60°,∠DFE=60°,
∴△DEF为等边三角形,故DE=DF=EF,
∵在△ADF和△CFE中,
∴△ADF≌△CFE(AAS),同理△CFE≌△BED,
故△ADF≌△CFE≌△BED,
∴BD=AF,
∴BD=2AD,
故D点为线段AB的三等分点.
微课程:勾股定理的逆定理同步练习参考答案
1. A 解析:根据勾股定理的逆定理进行判断。
2. D 解析: 关键能把BD放到特殊的模型中。∠ECD为60°,是△BCD的一个外角,而
CB=CD,得∠DBC=30°,则△BDE为直角三角形!DE=4,BE=8,则BD2=BE2-DE2。
*3. C 解析:勾股数一定为正整数,所以当15为最大边时有,,。当为最大边时,。显然不为整数,所以。
**4. D 解析:连接AC。在△ADC中,由于AD2=12+22=5,CD2=22+42=20,AC2=52=25。所以AD2+CD2=AC2,即△ADC是直角三角形。所以AD与CD之间是垂直关系。
5. 4cm 解析:根据勾股定理的逆定理进行判断。
6. 解析:,所以a=5,b=12,c=13。
因为 ,所以△ABC为直角三角形。
*7. 解析:因为,
,即所以△ABC是直角三角形,∠A 为直角。
8. (1)证明:∵Rt△ABC的面积为:ab或ch,
∴ab=ch,(ab)2=(ch)2,即a2b2=c2h2,
∵a2+b2=c2,
∴a2b2=(a2+b2)h2,
∴=,
∴=,
∴=,
∴;
(2)证明:∵c2<c2+h2,a2+b2=c2,
∴a2+b2<c2+h2,
∵ab=ch
∴a2+b2+2ab<c2+h2+2ch,
∴(a+b)2<(c+h)2,
∴a+b<c+h
(3)是直角三角形。
证明:∵(c+h)2=c2+2ch+h2,
h2+(a+b)2=h2+a2+2ab+b2,
∵a2+b2=c2,(勾股定理)
ab=ch(面积公式推导)
∴c2+2ch+h2=h2+a2+2ab+b2,
∴(c+h)2=h2+(a+b)2,
∴根据勾股定理的逆定理可知,以h,c+h,a+b为边构成的三角形是直角三角形。
(答题时间:60分钟)
微课程:探索勾股定理同步练习
一、选择题
1. 如果直角三角形的三条边为2,4,a,那么a2的取值可以有( )
A. 0个 B. 1个 C. 2个 D. 3个
2. 一棵树在离地5米处断裂,树顶落在离树根12米处,问树断之前有多高( )米
A. 17 B. 17.5 C. 18 D. 20
*3. (本溪中考)如图,在直角△ABC中,,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交BC于点E,连接AE,则△ACE的周长为( )
A. 16 B. 15 C. 14 D. 13
二、填空题
4. △ABC中,∠C=90o,AB=3,则AB2+BC2+AC2=_______。
*5. 如图,两个正方形的面积分别是25cm2和169 cm2,则直角三角形中边BC=____cm。
*6. 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=6,BC=5,将四个这样的直角三角形中边长为6的直角边向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是_________。
三、解答题
**7. (温州中考)勾股定理有着悠久的历史,它曾引起很多人的兴趣。l955年希腊发行了二枚以勾股图为背景的邮票。所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理。在下图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4。作
△PQR使得∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边_PQ上,则我们可发现△CGF≌△CAB,那么QH2+RD2的长等于多少?
8. 如图在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则BC的值。
9. 在Rt△ABC中,∠C=90°,AC=6,点D是斜边AB中点,作DE⊥AB,交直线AC于点E.若∠A=30°,求线段CE的长;
微课程:勾股定理的推广同步练习
一、选择题
1. 如图,已知S1、S2和S3分别是以RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、S2和S3满足的关系式为( )
A. S1
*2. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( )
A. 30 B. 28 C. 56 D. 不能确定
**3. 如图是某几何体的三视图及相关数据,则判断正确的是 ( )
A. a>c B. b>c C. 4a2+b2=c2 D. a2+b2=c2
二、解答题
**4. (苏州中考)李卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②。图①中,∠B=90°,∠A=30°,BC=6cm;图②中,∠D=90°,∠E=45°,DE=4cm;图③是李卫同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动。在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合)。
(1)在△DEF沿AC方向移动的过程中,李卫同学发现:F、C两点间的距离逐渐_____。(填“不变”、“变大”或“变小”)
(2)李卫同学经过进一步地研究,编制了如下问题:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
图① 图② 图③
请你分别完成上述二个问题的解答过程。
5. 如图,在正△ABC的三边AB、BC、CA上分别有点D、E、F,若DE⊥BC,EF⊥AC,FD⊥AB,同时成立,求D点在AB上的位置.
微课程:勾股定理的逆定理同步练习
一、选择题
1. 三角形三边之长分别为(1)3,4,5;(2)9,40,41;(3)7,24,25;(4)13,84,85。其中能构成直角三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
2. (临沂中考)如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长的平方为( )
A. 3 B. 12 C. 27 D. 48
*3. 若9,,15是一组勾股数,则=( )
A. 8 B. 10 C. 12 D. 不确定
**4. 如图是由边长为1的小正方形组成的网格,则AD与CD的位置关系是( )
A. 相交不垂直 B. 相交成45° C. 相交成60° D. 垂直
二、填空题
5. 已知两线段长为5cm和3cm,当第三条线段取整数 时,这三条线段能组成一个直角三角形。
三、解答题
6. 若△ABC的三边a、b、c满足条件 ,试判断△ABC的形状。
*7. 在△ABC中,AC=2a,BC=a2+1,AB= a2-1,其中a>1,△ABC是不是直角三角形?如果是哪一个角是直角?
8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h。试说明:(1);(2)a+b<c+h;(3)判断以a+b、h、c+h为边的三角形的形状,并说明理由。
初二数学北师大版(2012教材)第一章 1.1-1.2 探索勾股定理;一定是直角三角形?同步练习参考答案
微课程:探索勾股定理同步练习参考答案
1. C 解析:因为该三角形为直角三角形,所以满足a2+b2 =c2。在三边中,a有可能为直角边,也有可能为斜边,所以应选C。
2. C 解析:在Rt△ABC中标出已知条件,从而由勾股定理求得AB的长,再加上5米可知树高为18米。
*3. A 解析:直角△ABC中,,AB=8,AC=6,所以BC=10,因为DE是AB边的垂直平分线,所以AE=BE;=AC+CE+EA= AC+CE+BE=AC+BC=16。
4. 18 解析:根据勾股定理得BC2+AC2=AB2,所以AB2+BC2+AC2=(BC2+AC2)+AB2=AB2+AB2=2AB 2 =2×3 2=18。
*5. 12 解析:因为∠ABC=90°,所以由勾股定理得AB 2+BC 2=AC 2,即有25+BC 2=169,BC=12。
*6. 76 解析:利用勾股定理可以直接求解。
**7. 16 解析:题中仅知AB长,估计要求的要想方法联系它,要求的是平方和形式,则若它们在同一个三角形中,就有可能用勾股定理,但不在一起,则想方法把它们(或它们的相等线段)放在同一三角形中。过点A作AM⊥QH于点M,则可得△HMA≌△ACB,得∠QHG=60°,RD=AM=BC;△GCF≌△ACB,得∠QGH=60°,则△QHG是等边三角形,得QH=HG=AC,则QH2+RD2=AC2+BC2=AB2=16。
8. 解:∵在△ADE和△ADC中,
∴△ADE≌△ADC(AAS),
∴CD=DE,∵BD=2CD,
∴BC=BD+CD=3DE=9.
∴BC=9.
答:线段BC的长为9.
9. 解:连接BE,点D是斜边AB中点且DE⊥AB,
∵∠A=30°,∴∠ABC=90°-30°=60°,
又∵DE垂直平分AB,
∴∠ABE=∠BAE=30°,∠CBE=∠ABC-∠ABE=30°,
又∵∠C=90°,∴CE=·BE=·AE,
∵AC=6,∴BE=AE=4,CE=BE=×4=2
答:线段CE的长为2。
微课程:勾股定理的推广同步练习参考答案
1. B 解析:三个半圆的面积为π(边长之半)2=π(边长)2,而两个小的(边长)2之和=(大的边长)2,则两个小的面积之和等于大的面积。
*2. D 解析:例如9,12,15;12,16,20都满足条件。
**3. D 解析:弄清楚三视图之间的关系,本题只要知道主视图和左视图中三角形的底是俯视图中圆的直径,再利用勾股定理可解。
**4. 解析:(1)变小。
(2)解:设AD=x,在Rt△FDC中,FC2=DC2+FD2=(12-x)2+16
(Ⅰ)当FC为斜边时,
由AD2+BC2=FC2得,x2+62=(12-x)2+16,x=
(Ⅱ)当AD为斜边时,
由AD2=FC2+BC2得,x2=(12-x)2+16+62,x=>8(不符合题意,舍去)。
(Ⅲ)当BC为斜边时,
∵FC>CD∴FC+AD>12
∴FC、AD中至少有一条线段的长度大于6,
∴BC不能为斜边,
∴由(Ⅰ)、(Ⅱ)、(Ⅲ)得,当时,经线段AD、FC、BC的长度为三边长的三角形是直角三角形。
5. 解:∵DE⊥BC,
∴∠BDE=90°-∠B=30°,BD=2BE,
∴∠EDF=60°,同理∠DEF=60°,∠DFE=60°,
∴△DEF为等边三角形,故DE=DF=EF,
∵在△ADF和△CFE中,
∴△ADF≌△CFE(AAS),同理△CFE≌△BED,
故△ADF≌△CFE≌△BED,
∴BD=AF,
∴BD=2AD,
故D点为线段AB的三等分点.
微课程:勾股定理的逆定理同步练习参考答案
1. A 解析:根据勾股定理的逆定理进行判断。
2. D 解析: 关键能把BD放到特殊的模型中。∠ECD为60°,是△BCD的一个外角,而
CB=CD,得∠DBC=30°,则△BDE为直角三角形!DE=4,BE=8,则BD2=BE2-DE2。
*3. C 解析:勾股数一定为正整数,所以当15为最大边时有,,。当为最大边时,。显然不为整数,所以。
**4. D 解析:连接AC。在△ADC中,由于AD2=12+22=5,CD2=22+42=20,AC2=52=25。所以AD2+CD2=AC2,即△ADC是直角三角形。所以AD与CD之间是垂直关系。
5. 4cm 解析:根据勾股定理的逆定理进行判断。
6. 解析:,所以a=5,b=12,c=13。
因为 ,所以△ABC为直角三角形。
*7. 解析:因为,
,即所以△ABC是直角三角形,∠A 为直角。
8. (1)证明:∵Rt△ABC的面积为:ab或ch,
∴ab=ch,(ab)2=(ch)2,即a2b2=c2h2,
∵a2+b2=c2,
∴a2b2=(a2+b2)h2,
∴=,
∴=,
∴=,
∴;
(2)证明:∵c2<c2+h2,a2+b2=c2,
∴a2+b2<c2+h2,
∵ab=ch
∴a2+b2+2ab<c2+h2+2ch,
∴(a+b)2<(c+h)2,
∴a+b<c+h
(3)是直角三角形。
证明:∵(c+h)2=c2+2ch+h2,
h2+(a+b)2=h2+a2+2ab+b2,
∵a2+b2=c2,(勾股定理)
ab=ch(面积公式推导)
∴c2+2ch+h2=h2+a2+2ab+b2,
∴(c+h)2=h2+(a+b)2,
∴根据勾股定理的逆定理可知,以h,c+h,a+b为边构成的三角形是直角三角形。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
