湘教版九年级数学上册第4章锐角三角函数单元测试(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册第4章锐角三角函数单元测试(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 00:00:00 | ||
图片预览



文档简介
检测内容:第4章
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列等式中正确的是(
)
A.cos
A=
B.sin
B=
C.tan
B=
D.以上都不正确
2.下列等式成立的是(
)
A.sin
45°+cos
45°=1
B.2tan
30°=tan
60°
C.2
sin
30°=
tan
45°
D.
sin
30°=cos
60°
3.在Rt△ABC中,∠C=90°,sin
A=,则tan
B的值为(
)
A.
B.
C.
D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10
m,楼高AB=24
m,则树CD的高约为(
)
A.5
m
B.6
m
C.7
m
D.8
m
5.如图,在?ABCD中,点E是AD的中点,延长BC到点F,使CF∶BC=1∶2,连接DF,EC.若AB=5,AD=8,sin
B=,则DF的长等于(
)
A.
B.
C.
D.2
6.如图,∠AOB的顶点在坐标原点,边OB与x轴正半轴重合,边OA落在第一象限,P为OA上一点,OP=m,∠AOB=β,则点P的坐标为(
)
A.(m+tan
β,)
B.(m
sin
β,m
cos
β)
C.(,m
tan
β)
D.(m
cos
β,m
sin
β)
7.(2019·泰安)如图,一艘船由A港沿北偏东65°方向航行30
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(
)
A.(30+30)km
B.(30+10)km
C.(10+30)km
D.(30)km
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan
∠CFB的值等于(
)
A.
B.
C.
D.5
二、填空题(每小题3分,共24分)
9.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=(
).
10.在Rt△ABC中,∠C=90°,cos
B=,则a∶b=(
).
11.
(2019·乐山)如图,在△ABC中,∠B=30°,AC=2,cos
C=.则AB边的长为(
).
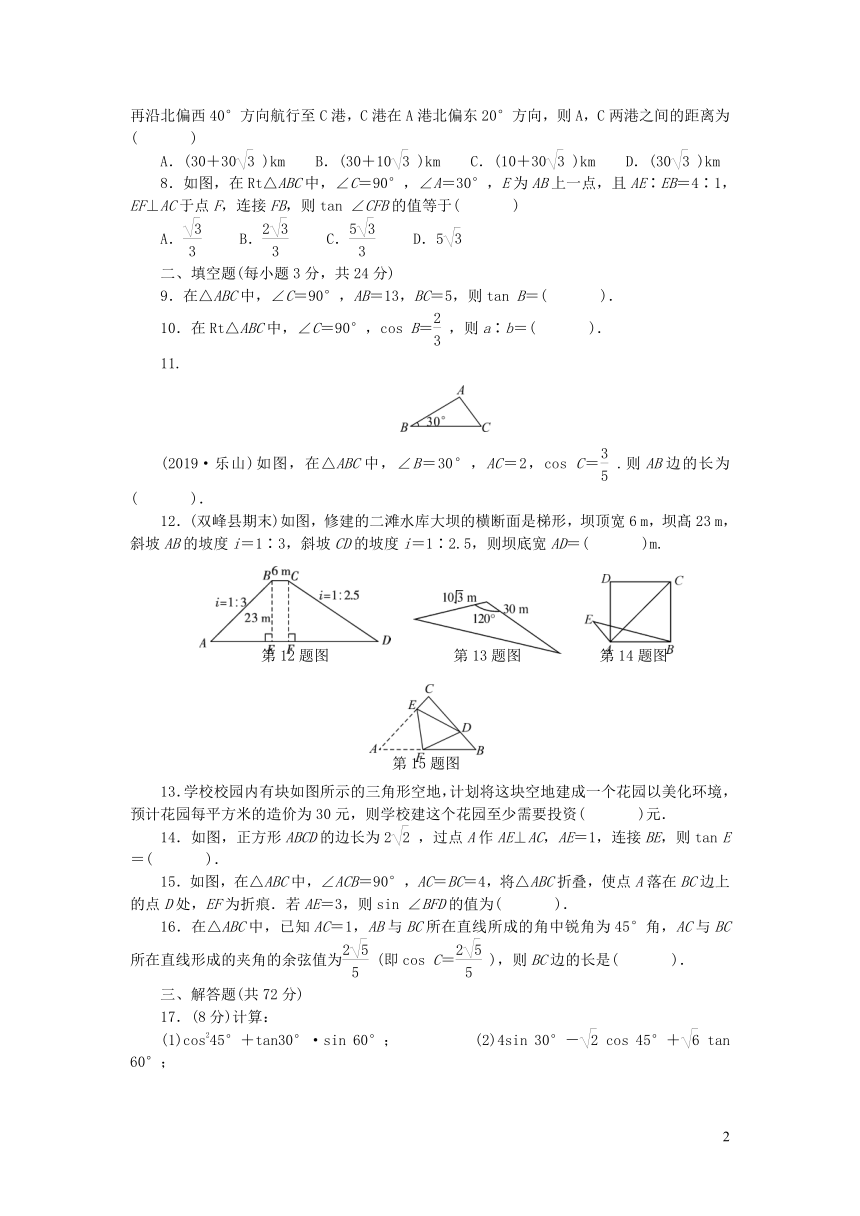
12.(双峰县期末)如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝髙23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,则坝底宽AD=(
)m.
13.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园以美化环境,预计花园每平方米的造价为30元,则学校建这个花园至少需要投资(
)元.
14.如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tan
E=(
).
15.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin
∠BFD的值为(
).
16.在△ABC中,已知AC=1,AB与BC所在直线所成的角中锐角为45°角,AC与BC所在直线形成的夹角的余弦值为(即cos
C=),则BC边的长是(
).
三、解答题(共72分)
17.(8分)计算:
(1)cos245°+tan30°·sin
60°; (2)4sin
30°-cos
45°+tan
60°;
(3)+2cos230°;
(4)-+tan
45°.
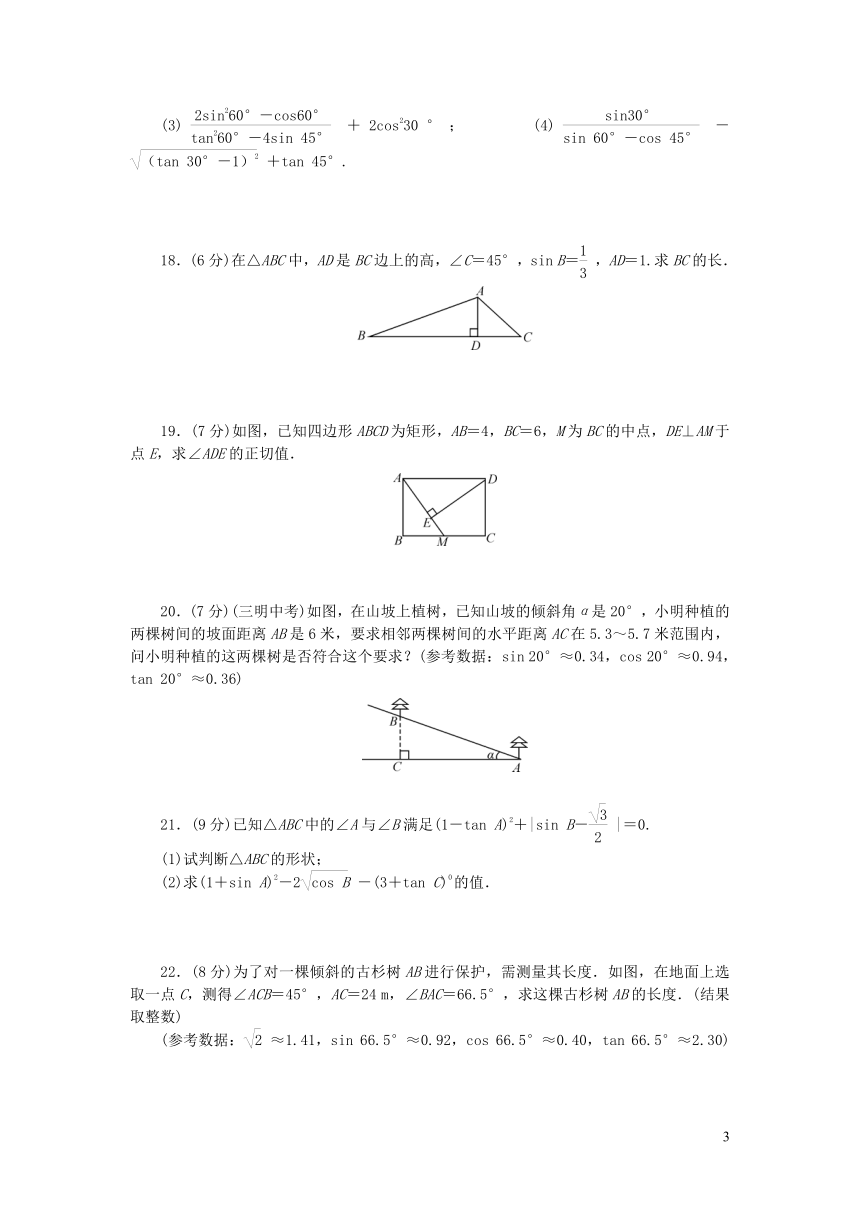
18.(6分)在△ABC中,AD是BC边上的高,∠C=45°,sin
B=,AD=1.求BC的长.
19.(7分)如图,已知四边形ABCD为矩形,AB=4,BC=6,M为BC的中点,DE⊥AM于点E,求∠ADE的正切值.
20.(7分)(三明中考)如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?(参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)
21.(9分)已知△ABC中的∠A与∠B满足(1-tan
A)2+|sin
B-|=0.
(1)试判断△ABC的形状;
(2)求(1+sin
A)2-2-(3+tan
C)0的值.
22.(8分)为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24
m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
(参考数据:≈1.41,sin
66.5°≈0.92,cos
66.5°≈0.40,tan
66.5°≈2.30)
23.(9分)(连云港中考)如图①,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图②,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
24.(9分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin
36.5°≈0.6,cos
36.5°≈0.8,tan
36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
25.(10分)如图①所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图②,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20
cm,且AH=DE=EG=20
cm.
(1)当∠CED=60°时,求C,D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1
cm)
(3)设DG=x
cm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1
cm)(参考数据≈1.732,可使用科学计算器)
检测内容:第4章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列等式中正确的是(D)
A.cos
A=
B.sin
B=
C.tan
B=
D.以上都不正确
2.下列等式成立的是(C)
A.sin
45°+cos
45°=1
B.2tan
30°=tan
60°
C.2
sin
30°=
tan
45°
D.
sin
30°=cos
60°
3.在Rt△ABC中,∠C=90°,sin
A=,则tan
B的值为(D)
A.
B.
C.
D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10
m,楼高AB=24
m,则树CD的高约为(C)
A.5
m
B.6
m
C.7
m
D.8
m
5.如图,在?ABCD中,点E是AD的中点,延长BC到点F,使CF∶BC=1∶2,连接DF,EC.若AB=5,AD=8,sin
B=,则DF的长等于(C)
A.
B.
C.
D.2
6.如图,∠AOB的顶点在坐标原点,边OB与x轴正半轴重合,边OA落在第一象限,P为OA上一点,OP=m,∠AOB=β,则点P的坐标为(D)
A.(m+tan
β,)
B.(m
sin
β,m
cos
β)
C.(,m
tan
β)
D.(m
cos
β,m
sin
β)
7.(2019·泰安)如图,一艘船由A港沿北偏东65°方向航行30
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(
B
)
A.(30+30)km
B.(30+10)km
C.(10+30)km
D.(30)km
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan
∠CFB的值等于(C)
A.
B.
C.
D.5
二、填空题(每小题3分,共24分)
9.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=____.
10.在Rt△ABC中,∠C=90°,cos
B=,则a∶b=__2∶__.
11.
(2019·乐山)如图,在△ABC中,∠B=30°,AC=2,cos
C=.则AB边的长为____.
12.(双峰县期末)如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝髙23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,则坝底宽AD=132.5m.
13.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园以美化环境,预计花园每平方米的造价为30元,则学校建这个花园至少需要投资__6_750__元.
14.如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tan
E=____.
15.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin
∠BFD的值为____.
16.在△ABC中,已知AC=1,AB与BC所在直线所成的角中锐角为45°角,AC与BC所在直线形成的夹角的余弦值为(即cos
C=),则BC边的长是__或__.
三、解答题(共72分)
17.(8分)计算:
(1)cos245°+tan30°·sin
60°; (2)4sin
30°-cos
45°+tan
60°;
解:原式=1;
解:原式=1+3;
(3)+2cos230°;
(4)-+tan
45°.
解:原式=;
解:原式=+.
18.(6分)在△ABC中,AD是BC边上的高,∠C=45°,sin
B=,AD=1.求BC的长.
解:在Rt△ABD中,∵sin
B==,又∵AD=1,∴AB=3.∵BD2=AB2-AD2,∴BD==2.在Rt△ADC中,∵∠C=45°,∴CD=AD=1.∴BC=BD+DC=2+1.
19.(7分)如图,已知四边形ABCD为矩形,AB=4,BC=6,M为BC的中点,DE⊥AM于点E,求∠ADE的正切值.
解:易知△ABM∽△DEA,∴=,又AB=4
cm,BM=3
cm,
∴tan
∠ADE===.
20.(7分)(三明中考)如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?(参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)
解:Rt△ACB中,AB=6米,∠A=20°,∴AC=AB·cos
∠A≈6×0.94=5.64米.∵5.64米在5.3~5.7米范围内,∴小明种植的这两棵树符合要求.
21.(9分)已知△ABC中的∠A与∠B满足(1-tan
A)2+|sin
B-|=0.
(1)试判断△ABC的形状;
(2)求(1+sin
A)2-2-(3+tan
C)0的值.
解:(1)∵(1-tan
A)2+|sin
B-|=0,∴tan
A=1,sin
B=,∴∠A=45°,∠B=60°,
∴∠C=180°-45°-60°=75°,∴△ABC是锐角三角形.
(2)∵∠A=45°,∠B=60°,∠C=75°,∴原式=(1+)2-2×-1=.
22.(8分)为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24
m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
(参考数据:≈1.41,sin
66.5°≈0.92,cos
66.5°≈0.40,tan
66.5°≈2.30)
解:过B点作BD⊥AC于D.∵∠ACB=45°,∠BAC=66.5°.∴在Rt△ADB中,AD=.在Rt△CDB中,CD=BD,∵AC=AD+CD=24
m,∴+BD=24,解得BD≈17
m.又∵sin
∠BAC=,∴AB=≈18
m.故这棵古杉树AB的长度大约为18
m.
23.(9分)(连云港中考)如图①,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图②,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
解:(1)作DM⊥AB于点M,CN⊥AB于点N.由题意得tan
∠DAB==2,设AM=x,则DM=2x.∵四边形DMNC是矩形,∴DM=CN=2x.在Rt△NBC中,tan
37°===,∴BN=x.∵x+3+x=14,∴x=3,∴DM=6,答:坝高为6
m.
(2)作FH⊥AB于点H.设DF=y,则AE=2y,EH=2y+3-y=3+y,BH=14+2y-(3+y)=11+y.由FH⊥AB,EF⊥BF可得△EFH∽△FBH,所以=,即=,解得y=-7+2或-7-2(舍弃),∴DF=2-7,答:DF的长为(2-7)m.
24.(9分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin
36.5°≈0.6,cos
36.5°≈0.8,tan
36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
解:(1)过点P作PE⊥AB于点E,由题意得,∠PAE=36.5°,∠PBA=45°,设PE为x海里,则BE=PE=x海里,∵AB=140海里,∴AE=(140-x)海里,在Rt△PAE中,=tan
∠PAE,即=0.75,解得:x=60海里,∴可疑漂浮物P到A,B两船所在直线的距离为60海里;(2)在Rt△PBE中,PE=60海里,∠PBE=45°,则BP=PE=60≈84.8海里,B船到达P处需要的时间为≈2.83小时.在Rt△PAE中,=sin
∠PAE,∴AP=PE÷sin
∠PAE=60÷0.6=100海里,∴A船到达P处需要的时间为100÷40=2.5小时.∵2.83>2.5,∴A船先到达P处.
25.(10分)如图①所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图②,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20
cm,且AH=DE=EG=20
cm.
(1)当∠CED=60°时,求C,D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1
cm)
(3)设DG=x
cm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1
cm)(参考数据≈1.732,可使用科学计算器)
解:(1)连接CD.∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20
cm;(2)根据题意得:AB=BC=CD,当∠CED=60°时,AD=3CD=60
cm,当∠CED=120°时,过点E作EH⊥CD于H,则∠CEH=60°,CH=HD.在直角△CHE中,sin
∠CEH=,∴CH=20·sin60°=20×=10(cm),∴CD=20
cm,∴AD=3×20=60≈103.9(cm),即点A向左移动了103.9-60=43.9
cm;(3)当∠CED=120°时,∠DEG=60°,∵DE=EG,∴△DEG是等边三角形,∴DG=DE=20
cm,当∠CED=60°时,则有∠DEG=120°,过点E作EI⊥DG于点I,∵DE=EG,∴∠DEI=∠GEI=60°,DI=IG,在直角△DIE中,sin
∠DEI=,∴DI=DE·sin
∠DEI=20×sin
60°=20×=10cm.∴DG=2DI=20≈34.6
cm.故x的范围是20
cm≤x≤34.6
cm.
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列等式中正确的是(
)
A.cos
A=
B.sin
B=
C.tan
B=
D.以上都不正确
2.下列等式成立的是(
)
A.sin
45°+cos
45°=1
B.2tan
30°=tan
60°
C.2
sin
30°=
tan
45°
D.
sin
30°=cos
60°
3.在Rt△ABC中,∠C=90°,sin
A=,则tan
B的值为(
)
A.
B.
C.
D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10
m,楼高AB=24
m,则树CD的高约为(
)
A.5
m
B.6
m
C.7
m
D.8
m
5.如图,在?ABCD中,点E是AD的中点,延长BC到点F,使CF∶BC=1∶2,连接DF,EC.若AB=5,AD=8,sin
B=,则DF的长等于(
)
A.
B.
C.
D.2
6.如图,∠AOB的顶点在坐标原点,边OB与x轴正半轴重合,边OA落在第一象限,P为OA上一点,OP=m,∠AOB=β,则点P的坐标为(
)
A.(m+tan
β,)
B.(m
sin
β,m
cos
β)
C.(,m
tan
β)
D.(m
cos
β,m
sin
β)
7.(2019·泰安)如图,一艘船由A港沿北偏东65°方向航行30
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(
)
A.(30+30)km
B.(30+10)km
C.(10+30)km
D.(30)km
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan
∠CFB的值等于(
)
A.
B.
C.
D.5
二、填空题(每小题3分,共24分)
9.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=(
).
10.在Rt△ABC中,∠C=90°,cos
B=,则a∶b=(
).
11.
(2019·乐山)如图,在△ABC中,∠B=30°,AC=2,cos
C=.则AB边的长为(
).
12.(双峰县期末)如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝髙23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,则坝底宽AD=(
)m.
13.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园以美化环境,预计花园每平方米的造价为30元,则学校建这个花园至少需要投资(
)元.
14.如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tan
E=(
).
15.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin
∠BFD的值为(
).
16.在△ABC中,已知AC=1,AB与BC所在直线所成的角中锐角为45°角,AC与BC所在直线形成的夹角的余弦值为(即cos
C=),则BC边的长是(
).
三、解答题(共72分)
17.(8分)计算:
(1)cos245°+tan30°·sin
60°; (2)4sin
30°-cos
45°+tan
60°;
(3)+2cos230°;
(4)-+tan
45°.
18.(6分)在△ABC中,AD是BC边上的高,∠C=45°,sin
B=,AD=1.求BC的长.
19.(7分)如图,已知四边形ABCD为矩形,AB=4,BC=6,M为BC的中点,DE⊥AM于点E,求∠ADE的正切值.
20.(7分)(三明中考)如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?(参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)
21.(9分)已知△ABC中的∠A与∠B满足(1-tan
A)2+|sin
B-|=0.
(1)试判断△ABC的形状;
(2)求(1+sin
A)2-2-(3+tan
C)0的值.
22.(8分)为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24
m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
(参考数据:≈1.41,sin
66.5°≈0.92,cos
66.5°≈0.40,tan
66.5°≈2.30)
23.(9分)(连云港中考)如图①,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图②,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
24.(9分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin
36.5°≈0.6,cos
36.5°≈0.8,tan
36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
25.(10分)如图①所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图②,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20
cm,且AH=DE=EG=20
cm.
(1)当∠CED=60°时,求C,D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1
cm)
(3)设DG=x
cm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1
cm)(参考数据≈1.732,可使用科学计算器)
检测内容:第4章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列等式中正确的是(D)
A.cos
A=
B.sin
B=
C.tan
B=
D.以上都不正确
2.下列等式成立的是(C)
A.sin
45°+cos
45°=1
B.2tan
30°=tan
60°
C.2
sin
30°=
tan
45°
D.
sin
30°=cos
60°
3.在Rt△ABC中,∠C=90°,sin
A=,则tan
B的值为(D)
A.
B.
C.
D.
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10
m,楼高AB=24
m,则树CD的高约为(C)
A.5
m
B.6
m
C.7
m
D.8
m
5.如图,在?ABCD中,点E是AD的中点,延长BC到点F,使CF∶BC=1∶2,连接DF,EC.若AB=5,AD=8,sin
B=,则DF的长等于(C)
A.
B.
C.
D.2
6.如图,∠AOB的顶点在坐标原点,边OB与x轴正半轴重合,边OA落在第一象限,P为OA上一点,OP=m,∠AOB=β,则点P的坐标为(D)
A.(m+tan
β,)
B.(m
sin
β,m
cos
β)
C.(,m
tan
β)
D.(m
cos
β,m
sin
β)
7.(2019·泰安)如图,一艘船由A港沿北偏东65°方向航行30
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(
B
)
A.(30+30)km
B.(30+10)km
C.(10+30)km
D.(30)km
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan
∠CFB的值等于(C)
A.
B.
C.
D.5
二、填空题(每小题3分,共24分)
9.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=____.
10.在Rt△ABC中,∠C=90°,cos
B=,则a∶b=__2∶__.
11.
(2019·乐山)如图,在△ABC中,∠B=30°,AC=2,cos
C=.则AB边的长为____.
12.(双峰县期末)如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6
m,坝髙23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,则坝底宽AD=132.5m.
13.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园以美化环境,预计花园每平方米的造价为30元,则学校建这个花园至少需要投资__6_750__元.
14.如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tan
E=____.
15.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin
∠BFD的值为____.
16.在△ABC中,已知AC=1,AB与BC所在直线所成的角中锐角为45°角,AC与BC所在直线形成的夹角的余弦值为(即cos
C=),则BC边的长是__或__.
三、解答题(共72分)
17.(8分)计算:
(1)cos245°+tan30°·sin
60°; (2)4sin
30°-cos
45°+tan
60°;
解:原式=1;
解:原式=1+3;
(3)+2cos230°;
(4)-+tan
45°.
解:原式=;
解:原式=+.
18.(6分)在△ABC中,AD是BC边上的高,∠C=45°,sin
B=,AD=1.求BC的长.
解:在Rt△ABD中,∵sin
B==,又∵AD=1,∴AB=3.∵BD2=AB2-AD2,∴BD==2.在Rt△ADC中,∵∠C=45°,∴CD=AD=1.∴BC=BD+DC=2+1.
19.(7分)如图,已知四边形ABCD为矩形,AB=4,BC=6,M为BC的中点,DE⊥AM于点E,求∠ADE的正切值.
解:易知△ABM∽△DEA,∴=,又AB=4
cm,BM=3
cm,
∴tan
∠ADE===.
20.(7分)(三明中考)如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?(参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)
解:Rt△ACB中,AB=6米,∠A=20°,∴AC=AB·cos
∠A≈6×0.94=5.64米.∵5.64米在5.3~5.7米范围内,∴小明种植的这两棵树符合要求.
21.(9分)已知△ABC中的∠A与∠B满足(1-tan
A)2+|sin
B-|=0.
(1)试判断△ABC的形状;
(2)求(1+sin
A)2-2-(3+tan
C)0的值.
解:(1)∵(1-tan
A)2+|sin
B-|=0,∴tan
A=1,sin
B=,∴∠A=45°,∠B=60°,
∴∠C=180°-45°-60°=75°,∴△ABC是锐角三角形.
(2)∵∠A=45°,∠B=60°,∠C=75°,∴原式=(1+)2-2×-1=.
22.(8分)为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24
m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
(参考数据:≈1.41,sin
66.5°≈0.92,cos
66.5°≈0.40,tan
66.5°≈2.30)
解:过B点作BD⊥AC于D.∵∠ACB=45°,∠BAC=66.5°.∴在Rt△ADB中,AD=.在Rt△CDB中,CD=BD,∵AC=AD+CD=24
m,∴+BD=24,解得BD≈17
m.又∵sin
∠BAC=,∴AB=≈18
m.故这棵古杉树AB的长度大约为18
m.
23.(9分)(连云港中考)如图①,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3
m,背水坡AD的坡度i(即tan
∠DAB)为1∶0.5,坝底AB=14
m.
(1)求坝高;
(2)如图②,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin
37°≈,cos
37°≈,tan
37°≈)
解:(1)作DM⊥AB于点M,CN⊥AB于点N.由题意得tan
∠DAB==2,设AM=x,则DM=2x.∵四边形DMNC是矩形,∴DM=CN=2x.在Rt△NBC中,tan
37°===,∴BN=x.∵x+3+x=14,∴x=3,∴DM=6,答:坝高为6
m.
(2)作FH⊥AB于点H.设DF=y,则AE=2y,EH=2y+3-y=3+y,BH=14+2y-(3+y)=11+y.由FH⊥AB,EF⊥BF可得△EFH∽△FBH,所以=,即=,解得y=-7+2或-7-2(舍弃),∴DF=2-7,答:DF的长为(2-7)m.
24.(9分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin
36.5°≈0.6,cos
36.5°≈0.8,tan
36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
解:(1)过点P作PE⊥AB于点E,由题意得,∠PAE=36.5°,∠PBA=45°,设PE为x海里,则BE=PE=x海里,∵AB=140海里,∴AE=(140-x)海里,在Rt△PAE中,=tan
∠PAE,即=0.75,解得:x=60海里,∴可疑漂浮物P到A,B两船所在直线的距离为60海里;(2)在Rt△PBE中,PE=60海里,∠PBE=45°,则BP=PE=60≈84.8海里,B船到达P处需要的时间为≈2.83小时.在Rt△PAE中,=sin
∠PAE,∴AP=PE÷sin
∠PAE=60÷0.6=100海里,∴A船到达P处需要的时间为100÷40=2.5小时.∵2.83>2.5,∴A船先到达P处.
25.(10分)如图①所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图②,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20
cm,且AH=DE=EG=20
cm.
(1)当∠CED=60°时,求C,D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1
cm)
(3)设DG=x
cm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1
cm)(参考数据≈1.732,可使用科学计算器)
解:(1)连接CD.∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20
cm;(2)根据题意得:AB=BC=CD,当∠CED=60°时,AD=3CD=60
cm,当∠CED=120°时,过点E作EH⊥CD于H,则∠CEH=60°,CH=HD.在直角△CHE中,sin
∠CEH=,∴CH=20·sin60°=20×=10(cm),∴CD=20
cm,∴AD=3×20=60≈103.9(cm),即点A向左移动了103.9-60=43.9
cm;(3)当∠CED=120°时,∠DEG=60°,∵DE=EG,∴△DEG是等边三角形,∴DG=DE=20
cm,当∠CED=60°时,则有∠DEG=120°,过点E作EI⊥DG于点I,∵DE=EG,∴∠DEI=∠GEI=60°,DI=IG,在直角△DIE中,sin
∠DEI=,∴DI=DE·sin
∠DEI=20×sin
60°=20×=10cm.∴DG=2DI=20≈34.6
cm.故x的范围是20
cm≤x≤34.6
cm.
5
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
