湘教版九年级数学上册第3章图形的相似单元测试(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册第3章图形的相似单元测试(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 15:03:54 | ||
图片预览



文档简介
检测内容:第3章
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
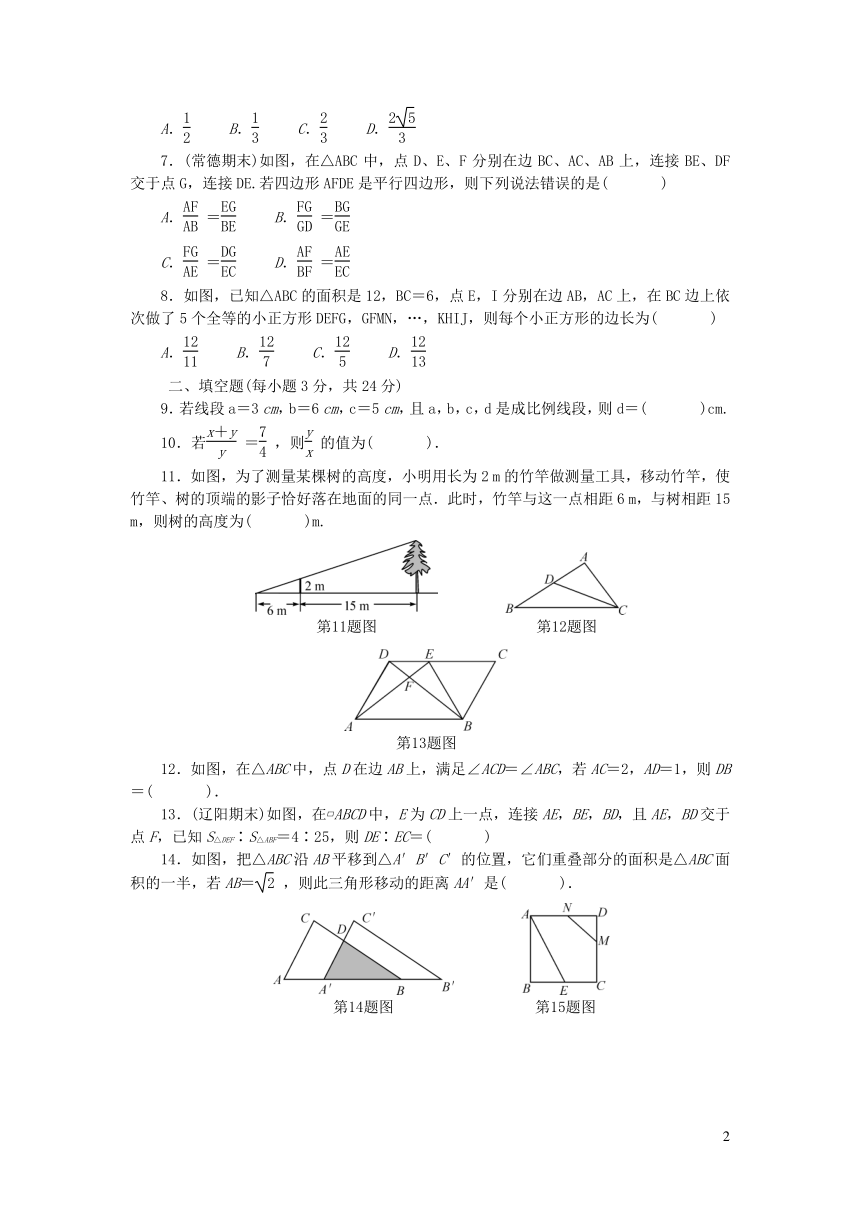
1.如图,DE∥BC,则下列比例式错误的是(
)
A.=
B.=
C.=
D.=
2.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于(
)
A.
B.
C.
D.
3.如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(
)
A.∠B=∠C
B.∠ADC=∠AEB
C.BD=CE,AB=AC
D.AD∶AB=AE∶AD
4.已知==(a≠0),那么(a+2b+3c)∶a等于(
)
A.8
B.9
C.10
D.11
5.如图是一个测量小玻璃管口径的量具ABC,AB的长为12
cm,AC被分为60等份,如果小玻璃管口DE正好对着量具的20等份处(DE∥AB),那么小玻璃管口径DE为(
)
A.8
cm
B.10
cm
C.20
cm
D.60
cm
6.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于(
)
A.
B.
C.
D.
7.(常德期末)如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是(
)
A.=
B.=
C.=
D.=
8.如图,已知△ABC的面积是12,BC=6,点E,I分别在边AB,AC上,在BC边上依次做了5个全等的小正方形DEFG,GFMN,…,KHIJ,则每个小正方形的边长为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
9.若线段a=3
cm,b=6
cm,c=5
cm,且a,b,c,d是成比例线段,则d=(
)cm.
10.若=,则的值为(
).
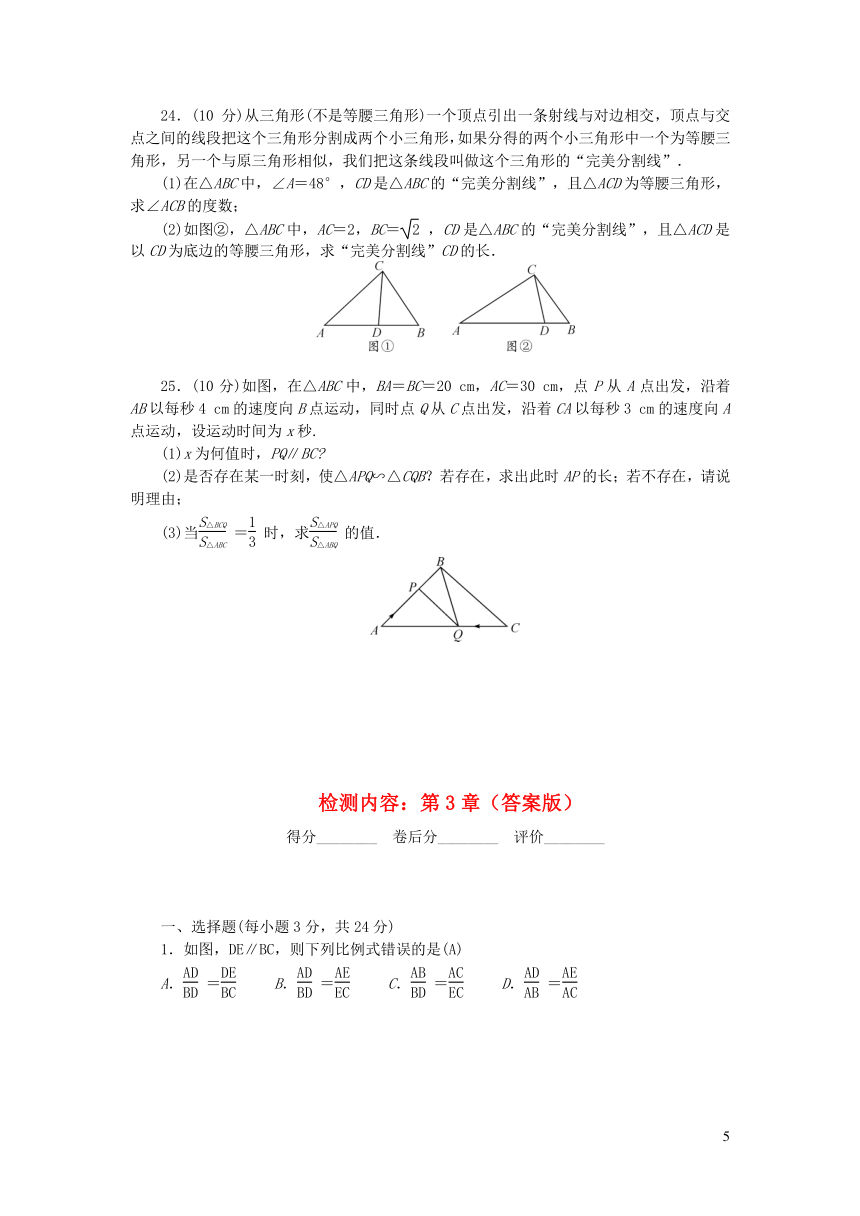
11.如图,为了测量某棵树的高度,小明用长为2
m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距6
m,与树相距15
m,则树的高度为(
)m.
12.如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=(
).
13.(辽阳期末)如图,在?ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,已知S△DEF∶S△ABF=4∶25,则DE∶EC=(
)
14.如图,把△ABC沿AB平移到△A′B′C′的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是(
).
15.如图所示,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=(
)时,△ABE与以D,M,N为顶点的三角形相似.
16.如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E点,且BE⊥CD,CE∶ED=2∶1.如果△BEC的面积为2,那么四边形ABED的面积是(
).
三、解答题(共72分)
17.(6分)如图,两平行线交∠A的一边于B,C两点,交∠A的另一边于D,M两点,已知AC+AB=14,且AM∶AD=4∶3,求AB的长.
18.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
19.(6分)如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.
20.(8分)(巴中中考)如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即SA1B1C1∶SA2B2C2=(
)
(不写解答过程,直接写出结果).
21.(8分)如图,马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移动到跷跷板PQ的什么位置时,狮子刚好将公鸡送到吊环上?
22.(8分)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E点.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
23.(10分)如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上的一点,且∠BAD=∠BGD=∠C,连接AD,AG,DG.求证:
(1)BD·BC=BG·BE;
(2)∠BGA=∠BAC.
24.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.
(1)在△ABC中,∠A=48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数;
(2)如图②,△ABC中,AC=2,BC=,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
25.(10分)如图,在△ABC中,BA=BC=20
cm,AC=30
cm,点P从A点出发,沿着AB以每秒4
cm的速度向B点运动,同时点Q从C点出发,沿着CA以每秒3
cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC?
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当=时,求的值.
检测内容:第3章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.如图,DE∥BC,则下列比例式错误的是(A)
A.=
B.=
C.=
D.=
2.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于(B)
A.
B.
C.
D.
3.如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(D)
A.∠B=∠C
B.∠ADC=∠AEB
C.BD=CE,AB=AC
D.AD∶AB=AE∶AD
4.已知==(a≠0),那么(a+2b+3c)∶a等于(C)
A.8
B.9
C.10
D.11
5.如图是一个测量小玻璃管口径的量具ABC,AB的长为12
cm,AC被分为60等份,如果小玻璃管口DE正好对着量具的20等份处(DE∥AB),那么小玻璃管口径DE为(A)
A.8
cm
B.10
cm
C.20
cm
D.60
cm
6.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于(A)
A.
B.
C.
D.
7.(常德期末)如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是(D)
A.=
B.=
C.=
D.=
8.如图,已知△ABC的面积是12,BC=6,点E,I分别在边AB,AC上,在BC边上依次做了5个全等的小正方形DEFG,GFMN,…,KHIJ,则每个小正方形的边长为(D)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
9.若线段a=3
cm,b=6
cm,c=5
cm,且a,b,c,d是成比例线段,则d=__10__cm.
10.若=,则的值为____.
11.如图,为了测量某棵树的高度,小明用长为2
m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距6
m,与树相距15
m,则树的高度为__7__m.
12.如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=__3__.
13.(辽阳期末)如图,在?ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,已知S△DEF∶S△ABF=4∶25,则DE∶EC=2∶3.
14.如图,把△ABC沿AB平移到△A′B′C′的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是__-1__.
15.如图所示,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=__或__时,△ABE与以D,M,N为顶点的三角形相似.
16.如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E点,且BE⊥CD,CE∶ED=2∶1.如果△BEC的面积为2,那么四边形ABED的面积是____.
三、解答题(共72分)
17.(6分)如图,两平行线交∠A的一边于B,C两点,交∠A的另一边于D,M两点,已知AC+AB=14,且AM∶AD=4∶3,求AB的长.
解:∵AM∶AD=4∶3,又BD∥CM,∴==.设AB=3x,AC=4x,又AC+AB=14,∴4x+3x=14,解得x=2,∴AB=3×2=6.
18.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
证明:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.又EF∥AB,∴∠B=∠CFE,∴∠ADE=∠CFE,又∠AED=∠C,∴△ADE∽△EFC.
19.(6分)如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.
证明:∵AD,BE是钝角△ABC的边BC,AC上的高,∴∠D=∠E=90°,∵∠ACD=∠BCE,∴△ACD∽△BCE,∴=.
20.(8分)(巴中中考)如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即SA1B1C1∶SA2B2C2=__1∶4__(不写解答过程,直接写出结果).
解:(1)略;(2)略.
21.(8分)如图,马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移动到跷跷板PQ的什么位置时,狮子刚好将公鸡送到吊环上?
解:(1)狮子能将公鸡送到吊环上.理由如下:过点Q作QH⊥PC,可证△PAB∽△PQH,得==,∴QH=2AB=2×1.2=2.4
m>2
m,因此狮子能将公鸡送到吊环上;(2)由(1)可知==,∴=,即当支点A移到跷跷板PQ靠近点P的处时,狮子刚好将公鸡送到吊环上.
22.(8分)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E点.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB,∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC,∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC;(2)∵AB=AD,又AE⊥BD,∴BE=DE,∴BD=2BE,由△ABE∽△DBC,得=,∵AB=AD=25,BC=32,∴=,∴BE=20(舍负值),∴AE===15.
23.(10分)如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上的一点,且∠BAD=∠BGD=∠C,连接AD,AG,DG.求证:
(1)BD·BC=BG·BE;
(2)∠BGA=∠BAC.
证明:(1)∵∠BGD=∠C,∠GBD=∠CBE,∴△BDG∽△BEC,∴=,∴BD·BC=BG·BE;
(2)∵∠BAD=∠C,∠ABD=∠CBA,∴△ABD∽△CBA,∴=,∴AB2=BD·BC.又由(1)知BD·BC=BG·BE,∴AB2=BG·BE,∴=.又∵∠GBA=∠ABE,∴△GBA∽△ABE,∴∠BGA=∠BAC.
24.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.
(1)在△ABC中,∠A=48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数;
(2)如图②,△ABC中,AC=2,BC=,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
解:(1)∵△BDC∽△BCA,∴∠BCD=∠A=48°.①当AD=CD时,∠ACD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°;②当AD=AC时,∠ACD=∠ADC==66°,∴∠ACB=∠ACD+∠BCD=114°;③当AC=CD时,∠ADC=∠A=48°=∠BCD,这与∠ADC=∠BCD+∠B相矛盾,舍去.∴∠ACB=96°或114°;
(2)由已知可知AC=AD=2,∵△BCD∽△BAC,∴==.∴BC2=BD·BA.设BD=x,∴()2=x(x+2),解得x=-1或x=--1(舍去).∴=,∴CD=×2=-.
25.(10分)如图,在△ABC中,BA=BC=20
cm,AC=30
cm,点P从A点出发,沿着AB以每秒4
cm的速度向B点运动,同时点Q从C点出发,沿着CA以每秒3
cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC?
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当=时,求的值.
解:(1)由题意知AP=4x,CQ=3x,若PQ∥BC,则△APQ∽△ABC,∴=,∵AB=BC=20,AC=30,∴AQ=30-3x,∵=,∴x=,∴当x=时,PQ∥BC;(2)存在.理由如下:∵△APQ∽△CQB,则=,∴=,∴9x2-10x=0,∴x1=0(舍去),x2=.∴当AP长为时,△APQ∽△CQB;(3)∵=,∴=,又AC=30,∴CQ=10,即3x=10,解得x=,此时,AP=4x=,∴==.∴==.
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.如图,DE∥BC,则下列比例式错误的是(
)
A.=
B.=
C.=
D.=
2.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于(
)
A.
B.
C.
D.
3.如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(
)
A.∠B=∠C
B.∠ADC=∠AEB
C.BD=CE,AB=AC
D.AD∶AB=AE∶AD
4.已知==(a≠0),那么(a+2b+3c)∶a等于(
)
A.8
B.9
C.10
D.11
5.如图是一个测量小玻璃管口径的量具ABC,AB的长为12
cm,AC被分为60等份,如果小玻璃管口DE正好对着量具的20等份处(DE∥AB),那么小玻璃管口径DE为(
)
A.8
cm
B.10
cm
C.20
cm
D.60
cm
6.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于(
)
A.
B.
C.
D.
7.(常德期末)如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是(
)
A.=
B.=
C.=
D.=
8.如图,已知△ABC的面积是12,BC=6,点E,I分别在边AB,AC上,在BC边上依次做了5个全等的小正方形DEFG,GFMN,…,KHIJ,则每个小正方形的边长为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
9.若线段a=3
cm,b=6
cm,c=5
cm,且a,b,c,d是成比例线段,则d=(
)cm.
10.若=,则的值为(
).
11.如图,为了测量某棵树的高度,小明用长为2
m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距6
m,与树相距15
m,则树的高度为(
)m.
12.如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=(
).
13.(辽阳期末)如图,在?ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,已知S△DEF∶S△ABF=4∶25,则DE∶EC=(
)
14.如图,把△ABC沿AB平移到△A′B′C′的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是(
).
15.如图所示,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=(
)时,△ABE与以D,M,N为顶点的三角形相似.
16.如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E点,且BE⊥CD,CE∶ED=2∶1.如果△BEC的面积为2,那么四边形ABED的面积是(
).
三、解答题(共72分)
17.(6分)如图,两平行线交∠A的一边于B,C两点,交∠A的另一边于D,M两点,已知AC+AB=14,且AM∶AD=4∶3,求AB的长.
18.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
19.(6分)如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.
20.(8分)(巴中中考)如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即SA1B1C1∶SA2B2C2=(
)
(不写解答过程,直接写出结果).
21.(8分)如图,马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移动到跷跷板PQ的什么位置时,狮子刚好将公鸡送到吊环上?
22.(8分)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E点.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
23.(10分)如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上的一点,且∠BAD=∠BGD=∠C,连接AD,AG,DG.求证:
(1)BD·BC=BG·BE;
(2)∠BGA=∠BAC.
24.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.
(1)在△ABC中,∠A=48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数;
(2)如图②,△ABC中,AC=2,BC=,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
25.(10分)如图,在△ABC中,BA=BC=20
cm,AC=30
cm,点P从A点出发,沿着AB以每秒4
cm的速度向B点运动,同时点Q从C点出发,沿着CA以每秒3
cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC?
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当=时,求的值.
检测内容:第3章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.如图,DE∥BC,则下列比例式错误的是(A)
A.=
B.=
C.=
D.=
2.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于(B)
A.
B.
C.
D.
3.如图,D,E分别是AB,AC上的点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是(D)
A.∠B=∠C
B.∠ADC=∠AEB
C.BD=CE,AB=AC
D.AD∶AB=AE∶AD
4.已知==(a≠0),那么(a+2b+3c)∶a等于(C)
A.8
B.9
C.10
D.11
5.如图是一个测量小玻璃管口径的量具ABC,AB的长为12
cm,AC被分为60等份,如果小玻璃管口DE正好对着量具的20等份处(DE∥AB),那么小玻璃管口径DE为(A)
A.8
cm
B.10
cm
C.20
cm
D.60
cm
6.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于(A)
A.
B.
C.
D.
7.(常德期末)如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是(D)
A.=
B.=
C.=
D.=
8.如图,已知△ABC的面积是12,BC=6,点E,I分别在边AB,AC上,在BC边上依次做了5个全等的小正方形DEFG,GFMN,…,KHIJ,则每个小正方形的边长为(D)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
9.若线段a=3
cm,b=6
cm,c=5
cm,且a,b,c,d是成比例线段,则d=__10__cm.
10.若=,则的值为____.
11.如图,为了测量某棵树的高度,小明用长为2
m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距6
m,与树相距15
m,则树的高度为__7__m.
12.如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=__3__.
13.(辽阳期末)如图,在?ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,已知S△DEF∶S△ABF=4∶25,则DE∶EC=2∶3.
14.如图,把△ABC沿AB平移到△A′B′C′的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是__-1__.
15.如图所示,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=__或__时,△ABE与以D,M,N为顶点的三角形相似.
16.如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E点,且BE⊥CD,CE∶ED=2∶1.如果△BEC的面积为2,那么四边形ABED的面积是____.
三、解答题(共72分)
17.(6分)如图,两平行线交∠A的一边于B,C两点,交∠A的另一边于D,M两点,已知AC+AB=14,且AM∶AD=4∶3,求AB的长.
解:∵AM∶AD=4∶3,又BD∥CM,∴==.设AB=3x,AC=4x,又AC+AB=14,∴4x+3x=14,解得x=2,∴AB=3×2=6.
18.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
证明:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.又EF∥AB,∴∠B=∠CFE,∴∠ADE=∠CFE,又∠AED=∠C,∴△ADE∽△EFC.
19.(6分)如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.
证明:∵AD,BE是钝角△ABC的边BC,AC上的高,∴∠D=∠E=90°,∵∠ACD=∠BCE,∴△ACD∽△BCE,∴=.
20.(8分)(巴中中考)如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即SA1B1C1∶SA2B2C2=__1∶4__(不写解答过程,直接写出结果).
解:(1)略;(2)略.
21.(8分)如图,马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移动到跷跷板PQ的什么位置时,狮子刚好将公鸡送到吊环上?
解:(1)狮子能将公鸡送到吊环上.理由如下:过点Q作QH⊥PC,可证△PAB∽△PQH,得==,∴QH=2AB=2×1.2=2.4
m>2
m,因此狮子能将公鸡送到吊环上;(2)由(1)可知==,∴=,即当支点A移到跷跷板PQ靠近点P的处时,狮子刚好将公鸡送到吊环上.
22.(8分)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E点.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB,∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC,∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC;(2)∵AB=AD,又AE⊥BD,∴BE=DE,∴BD=2BE,由△ABE∽△DBC,得=,∵AB=AD=25,BC=32,∴=,∴BE=20(舍负值),∴AE===15.
23.(10分)如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上的一点,且∠BAD=∠BGD=∠C,连接AD,AG,DG.求证:
(1)BD·BC=BG·BE;
(2)∠BGA=∠BAC.
证明:(1)∵∠BGD=∠C,∠GBD=∠CBE,∴△BDG∽△BEC,∴=,∴BD·BC=BG·BE;
(2)∵∠BAD=∠C,∠ABD=∠CBA,∴△ABD∽△CBA,∴=,∴AB2=BD·BC.又由(1)知BD·BC=BG·BE,∴AB2=BG·BE,∴=.又∵∠GBA=∠ABE,∴△GBA∽△ABE,∴∠BGA=∠BAC.
24.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.
(1)在△ABC中,∠A=48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数;
(2)如图②,△ABC中,AC=2,BC=,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
解:(1)∵△BDC∽△BCA,∴∠BCD=∠A=48°.①当AD=CD时,∠ACD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°;②当AD=AC时,∠ACD=∠ADC==66°,∴∠ACB=∠ACD+∠BCD=114°;③当AC=CD时,∠ADC=∠A=48°=∠BCD,这与∠ADC=∠BCD+∠B相矛盾,舍去.∴∠ACB=96°或114°;
(2)由已知可知AC=AD=2,∵△BCD∽△BAC,∴==.∴BC2=BD·BA.设BD=x,∴()2=x(x+2),解得x=-1或x=--1(舍去).∴=,∴CD=×2=-.
25.(10分)如图,在△ABC中,BA=BC=20
cm,AC=30
cm,点P从A点出发,沿着AB以每秒4
cm的速度向B点运动,同时点Q从C点出发,沿着CA以每秒3
cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC?
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当=时,求的值.
解:(1)由题意知AP=4x,CQ=3x,若PQ∥BC,则△APQ∽△ABC,∴=,∵AB=BC=20,AC=30,∴AQ=30-3x,∵=,∴x=,∴当x=时,PQ∥BC;(2)存在.理由如下:∵△APQ∽△CQB,则=,∴=,∴9x2-10x=0,∴x1=0(舍去),x2=.∴当AP长为时,△APQ∽△CQB;(3)∵=,∴=,又AC=30,∴CQ=10,即3x=10,解得x=,此时,AP=4x=,∴==.∴==.
5
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
