湘教版九年级数学上册第1章反比例函数单元测试(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册第1章反比例函数单元测试(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 00:00:00 | ||
图片预览




文档简介
检测内容:第1章
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.下列函数中,不是反比例函数的是(
)
A.y=
B.y=-(m≠0)
C.y=
D.y=
2.若反比例函数y=(k≠0)的图象过点(2,1),则这个函数的图象一定过点(
)
A.(2,-1)
B.(1,-2)
C.(-2,1)
D.(-2,-1)
3.已知反比例函数y=的图象经过点P(-1,2),则这个函数的图象位于(
)
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
4.已知反比例函数y=,下列结论错误的是(
)
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
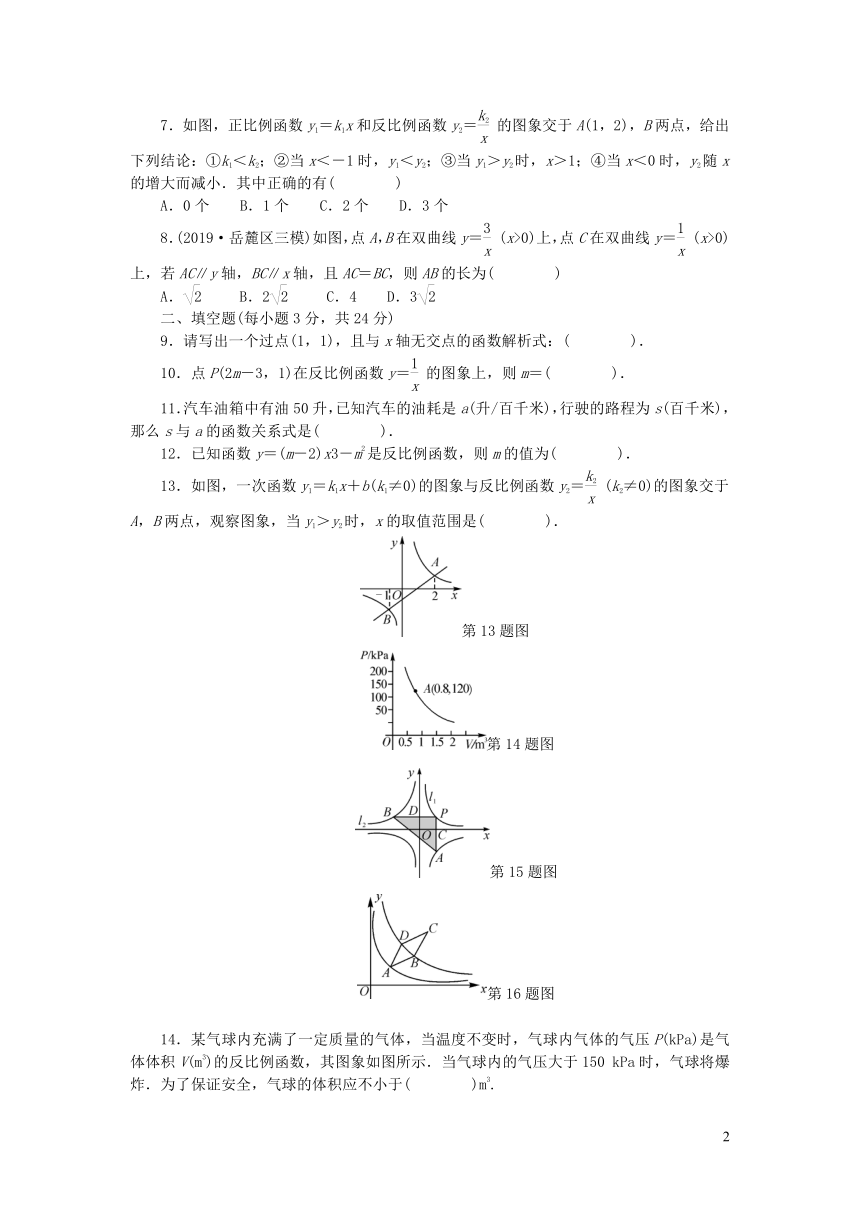
5.如图,一张正方形的纸片剪去两个一样的小长方形,得到一个“E”图案,设小长方形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是(
)
6.(怀化中考)已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是(
)
7.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,x>1;④当x<0时,y2随x的增大而减小.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
8.(2019·岳麓区三模)如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB的长为(
)
A.
B.2
C.4
D.3
二、填空题(每小题3分,共24分)
9.请写出一个过点(1,1),且与x轴无交点的函数解析式:(
).
10.点P(2m-3,1)在反比例函数y=的图象上,则m=(
).
11.汽车油箱中有油50升,已知汽车的油耗是a(升/百千米),行驶的路程为s(百千米),那么s与a的函数关系式是(
).
12.已知函数y=(m-2)x3-m2是反比例函数,则m的值为(
).
13.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是(
).
第13题图
第14题图
第15题图
第16题图
14.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150
kPa时,气球将爆炸.为了保证安全,气球的体积应不小于(
)m3.
15.如图,函数y=和y=-的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为(
).
16.(2019?福建)如图,菱形ABCD的顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B,D两点,若AB=2,∠BAD=30°,则k=(
).
三、解答题(共72分)
17.(8分)已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
18.(8分)小红家在七月初用购电卡买了1
000度电,设这些电够使用的天数为y,小红家平均每天的用电度数为x.
(1)求y关于x的函数表达式;
(2)若她家平均每天用电8度,则这些电可以用多长时间?
19.(8分)如图是反比例函数y=的图象的一支.
(1)根据图象画出反比例函数图象的另一支,并确定常数m的取值范围;
(2)若点A(m-3,b1)和点B(m-4,b2)是该反比例函数图象上的两点,请判断点A,B所在象限及b1与b2的大小,并说明判断理由.
20.(9分)在平面直角坐标系中,一次函数y=-x+b的图象与反比例函数y=(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的坐标为(-2,3).
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
21.(9分)已知y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=-1时,y=1.求x=-时,y的值.
22.(9分)(2019·襄阳)如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较大小:AD(
)BC(填“>”或“<”或“=”);
(3)直接写出y1<y2时,x的取值范围.
23.(10分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18
℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18
℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少摄氏度?
24.(11分)(镇江中考)六·一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A,B,C是弯道MN上的三点,矩形ADOG,矩形BEOH,矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数表达式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
检测内容:第1章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.下列函数中,不是反比例函数的是(C)
A.y=
B.y=-(m≠0)
C.y=
D.y=
2.若反比例函数y=(k≠0)的图象过点(2,1),则这个函数的图象一定过点(D)
A.(2,-1)
B.(1,-2)
C.(-2,1)
D.(-2,-1)
3.已知反比例函数y=的图象经过点P(-1,2),则这个函数的图象位于(D)
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
4.已知反比例函数y=,下列结论错误的是(B)
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
5.如图,一张正方形的纸片剪去两个一样的小长方形,得到一个“E”图案,设小长方形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是(
A
)
6.(怀化中考)已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是(C)
7.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,x>1;④当x<0时,y2随x的增大而减小.其中正确的有(C)
A.0个
B.1个
C.2个
D.3个
8.(2019·岳麓区三模)如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB的长为(B)
A.
B.2
C.4
D.3
二、填空题(每小题3分,共24分)
9.请写出一个过点(1,1),且与x轴无交点的函数解析式:y=.
10.点P(2m-3,1)在反比例函数y=的图象上,则m=__2__.
11.汽车油箱中有油50升,已知汽车的油耗是a(升/百千米),行驶的路程为s(百千米),那么s与a的函数关系式是__s=__.
12.已知函数y=(m-2)x3-m2是反比例函数,则m的值为__-2__.
13.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是__-1<x<0或x>2__.
第13题图
第14题图
第15题图
第16题图
14.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150
kPa时,气球将爆炸.为了保证安全,气球的体积应不小于__0.64__m3.
15.如图,函数y=和y=-的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为__8__.
16.(2019?福建)如图,菱形ABCD的顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B,D两点,若AB=2,∠BAD=30°,则k=6+2
.
三、解答题(共72分)
17.(8分)已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
解:(1)根据题意得k-1=1×2,解得k=3;(2)由题意得k-1>0,解得k>1.
18.(8分)小红家在七月初用购电卡买了1
000度电,设这些电够使用的天数为y,小红家平均每天的用电度数为x.
(1)求y关于x的函数表达式;
(2)若她家平均每天用电8度,则这些电可以用多长时间?
解:(1)根据题意可得x·y=1
000,即y=(x>0);(2)当x=8时,y==125,故这些电可以用125天.
19.(8分)如图是反比例函数y=的图象的一支.
(1)根据图象画出反比例函数图象的另一支,并确定常数m的取值范围;
(2)若点A(m-3,b1)和点B(m-4,b2)是该反比例函数图象上的两点,请判断点A,B所在象限及b1与b2的大小,并说明判断理由.
解:(1)∵反比例函数y=的图象的一支在第一象限,∴5-2m>0,解得m<.∵反比例函数的图象关于原点对称,据此可画出图象的另一支,图略;(2)点A,B在第三象限,b1<b2.理由如下:由(1)知m<,∴m-3<-,m-4<-,∴点A(m-3,b1)和点B(m-4,b2)都在第三象限的分支上.∵在第三象限内,y随x的增大而减小,且m-3>m-4,∴b1<b2.
20.(9分)在平面直角坐标系中,一次函数y=-x+b的图象与反比例函数y=(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的坐标为(-2,3).
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
解:(1)把(-2,3)分别代入y=-x+b,与y=中,有3=2+b,=3,解得b=1,k=-6,∴一次函数的解析式为y=-x+1,反比例函数的解析式为y=-;
(2)一次函数的解析式为y=-x+1,当x=0时,y=1,∴C(0,1),若将点C向上平移4个单位长度得到点F,则CF=4.∵一次函数y=-x+b的图象与反比例函数y=
(k≠0)的图象交于A、B两点,∴解得或∴B(3,-2),A(-2,3),
∴S△ABF=×4×(2+3)=10.
21.(9分)已知y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=-1时,y=1.求x=-时,y的值.
解:设y1=k1x2(k1≠0),y2=(k2≠0),∴y=k1x2+.由题意,得解得∴y=2x2+,当x=-时,y=-.
22.(9分)(2019·襄阳)如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较大小:AD__=__BC(填“>”或“<”或“=”);
(3)直接写出y1<y2时,x的取值范围.
解:(1)把A(3,4)代入反比例函数y2=,解得m=12,∴反比例函数的解析式为y2=;∵B(a,-2)点在反比例函数y2=的图象上,∴-2a=12,解得a=-6,∴B(-6,-2),∵一次函数y1=kx+b的图象经过A(3,4),B(-6,-2)两点,∴解得∴一次函数的解析式为y1=x+2;
(2)由一次函数的解析式为y1=x+2可知C(0,2),D(-3,0),∴AD==2,BC==2,∴AD=BC;
(3)由图象可知:y1<y2时x的取值范围是x<-6或0<x<3.
23.(10分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18
℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18
℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少摄氏度?
解:(1)恒温系统在这天保持大棚温度为18
℃的时间为12-2=10(小时);(2)∵点B(12,18)在双曲线y=上,∴18=,解得k=216;(3)由(2)得y=,∴当x=16时,大棚内的温度为=13.5
(℃).
24.(11分)(镇江中考)六·一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A,B,C是弯道MN上的三点,矩形ADOG,矩形BEOH,矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数表达式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
解:(1)∵矩形ADOG、矩形BEOH、矩形CFOI的面积相等,∴弯道为反比例函数图象的一部分.设函数表达式为y=(k≠0),OG=GH=HI=a,则AG=,BH=,CI=,所以S2=·a-·a=6,解得k=36,所以S1=·a-·a=k=×36=18,S3=·a=k=×36=12;(2)∵k=36,∴弯道函数表达式为y=.∵T(x,y)是弯道MN上的任一点,∴y=;(3)∵MP=2米,NQ=3米,∴GM==18,=3,解得OQ=12.∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),∴x=2时,y=18,可以种8棵,x=4时,y=9,可以种4棵,x=6时,y=6,可以种2棵,x=8时,y=4.5,可以种2棵,x=10时,y=3.6,可以种1棵.故一共能种植17棵花木.
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.下列函数中,不是反比例函数的是(
)
A.y=
B.y=-(m≠0)
C.y=
D.y=
2.若反比例函数y=(k≠0)的图象过点(2,1),则这个函数的图象一定过点(
)
A.(2,-1)
B.(1,-2)
C.(-2,1)
D.(-2,-1)
3.已知反比例函数y=的图象经过点P(-1,2),则这个函数的图象位于(
)
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
4.已知反比例函数y=,下列结论错误的是(
)
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
5.如图,一张正方形的纸片剪去两个一样的小长方形,得到一个“E”图案,设小长方形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是(
)
6.(怀化中考)已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是(
)
7.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,x>1;④当x<0时,y2随x的增大而减小.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
8.(2019·岳麓区三模)如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB的长为(
)
A.
B.2
C.4
D.3
二、填空题(每小题3分,共24分)
9.请写出一个过点(1,1),且与x轴无交点的函数解析式:(
).
10.点P(2m-3,1)在反比例函数y=的图象上,则m=(
).
11.汽车油箱中有油50升,已知汽车的油耗是a(升/百千米),行驶的路程为s(百千米),那么s与a的函数关系式是(
).
12.已知函数y=(m-2)x3-m2是反比例函数,则m的值为(
).
13.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是(
).
第13题图
第14题图
第15题图
第16题图
14.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150
kPa时,气球将爆炸.为了保证安全,气球的体积应不小于(
)m3.
15.如图,函数y=和y=-的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为(
).
16.(2019?福建)如图,菱形ABCD的顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B,D两点,若AB=2,∠BAD=30°,则k=(
).
三、解答题(共72分)
17.(8分)已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
18.(8分)小红家在七月初用购电卡买了1
000度电,设这些电够使用的天数为y,小红家平均每天的用电度数为x.
(1)求y关于x的函数表达式;
(2)若她家平均每天用电8度,则这些电可以用多长时间?
19.(8分)如图是反比例函数y=的图象的一支.
(1)根据图象画出反比例函数图象的另一支,并确定常数m的取值范围;
(2)若点A(m-3,b1)和点B(m-4,b2)是该反比例函数图象上的两点,请判断点A,B所在象限及b1与b2的大小,并说明判断理由.
20.(9分)在平面直角坐标系中,一次函数y=-x+b的图象与反比例函数y=(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的坐标为(-2,3).
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
21.(9分)已知y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=-1时,y=1.求x=-时,y的值.
22.(9分)(2019·襄阳)如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较大小:AD(
)BC(填“>”或“<”或“=”);
(3)直接写出y1<y2时,x的取值范围.
23.(10分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18
℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18
℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少摄氏度?
24.(11分)(镇江中考)六·一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A,B,C是弯道MN上的三点,矩形ADOG,矩形BEOH,矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数表达式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
检测内容:第1章(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共24分)
1.下列函数中,不是反比例函数的是(C)
A.y=
B.y=-(m≠0)
C.y=
D.y=
2.若反比例函数y=(k≠0)的图象过点(2,1),则这个函数的图象一定过点(D)
A.(2,-1)
B.(1,-2)
C.(-2,1)
D.(-2,-1)
3.已知反比例函数y=的图象经过点P(-1,2),则这个函数的图象位于(D)
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
4.已知反比例函数y=,下列结论错误的是(B)
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
5.如图,一张正方形的纸片剪去两个一样的小长方形,得到一个“E”图案,设小长方形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是(
A
)
6.(怀化中考)已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是(C)
7.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,x>1;④当x<0时,y2随x的增大而减小.其中正确的有(C)
A.0个
B.1个
C.2个
D.3个
8.(2019·岳麓区三模)如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB的长为(B)
A.
B.2
C.4
D.3
二、填空题(每小题3分,共24分)
9.请写出一个过点(1,1),且与x轴无交点的函数解析式:y=.
10.点P(2m-3,1)在反比例函数y=的图象上,则m=__2__.
11.汽车油箱中有油50升,已知汽车的油耗是a(升/百千米),行驶的路程为s(百千米),那么s与a的函数关系式是__s=__.
12.已知函数y=(m-2)x3-m2是反比例函数,则m的值为__-2__.
13.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是__-1<x<0或x>2__.
第13题图
第14题图
第15题图
第16题图
14.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150
kPa时,气球将爆炸.为了保证安全,气球的体积应不小于__0.64__m3.
15.如图,函数y=和y=-的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为__8__.
16.(2019?福建)如图,菱形ABCD的顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B,D两点,若AB=2,∠BAD=30°,则k=6+2
.
三、解答题(共72分)
17.(8分)已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
解:(1)根据题意得k-1=1×2,解得k=3;(2)由题意得k-1>0,解得k>1.
18.(8分)小红家在七月初用购电卡买了1
000度电,设这些电够使用的天数为y,小红家平均每天的用电度数为x.
(1)求y关于x的函数表达式;
(2)若她家平均每天用电8度,则这些电可以用多长时间?
解:(1)根据题意可得x·y=1
000,即y=(x>0);(2)当x=8时,y==125,故这些电可以用125天.
19.(8分)如图是反比例函数y=的图象的一支.
(1)根据图象画出反比例函数图象的另一支,并确定常数m的取值范围;
(2)若点A(m-3,b1)和点B(m-4,b2)是该反比例函数图象上的两点,请判断点A,B所在象限及b1与b2的大小,并说明判断理由.
解:(1)∵反比例函数y=的图象的一支在第一象限,∴5-2m>0,解得m<.∵反比例函数的图象关于原点对称,据此可画出图象的另一支,图略;(2)点A,B在第三象限,b1<b2.理由如下:由(1)知m<,∴m-3<-,m-4<-,∴点A(m-3,b1)和点B(m-4,b2)都在第三象限的分支上.∵在第三象限内,y随x的增大而减小,且m-3>m-4,∴b1<b2.
20.(9分)在平面直角坐标系中,一次函数y=-x+b的图象与反比例函数y=(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的坐标为(-2,3).
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
解:(1)把(-2,3)分别代入y=-x+b,与y=中,有3=2+b,=3,解得b=1,k=-6,∴一次函数的解析式为y=-x+1,反比例函数的解析式为y=-;
(2)一次函数的解析式为y=-x+1,当x=0时,y=1,∴C(0,1),若将点C向上平移4个单位长度得到点F,则CF=4.∵一次函数y=-x+b的图象与反比例函数y=
(k≠0)的图象交于A、B两点,∴解得或∴B(3,-2),A(-2,3),
∴S△ABF=×4×(2+3)=10.
21.(9分)已知y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=-1时,y=1.求x=-时,y的值.
解:设y1=k1x2(k1≠0),y2=(k2≠0),∴y=k1x2+.由题意,得解得∴y=2x2+,当x=-时,y=-.
22.(9分)(2019·襄阳)如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较大小:AD__=__BC(填“>”或“<”或“=”);
(3)直接写出y1<y2时,x的取值范围.
解:(1)把A(3,4)代入反比例函数y2=,解得m=12,∴反比例函数的解析式为y2=;∵B(a,-2)点在反比例函数y2=的图象上,∴-2a=12,解得a=-6,∴B(-6,-2),∵一次函数y1=kx+b的图象经过A(3,4),B(-6,-2)两点,∴解得∴一次函数的解析式为y1=x+2;
(2)由一次函数的解析式为y1=x+2可知C(0,2),D(-3,0),∴AD==2,BC==2,∴AD=BC;
(3)由图象可知:y1<y2时x的取值范围是x<-6或0<x<3.
23.(10分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18
℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18
℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少摄氏度?
解:(1)恒温系统在这天保持大棚温度为18
℃的时间为12-2=10(小时);(2)∵点B(12,18)在双曲线y=上,∴18=,解得k=216;(3)由(2)得y=,∴当x=16时,大棚内的温度为=13.5
(℃).
24.(11分)(镇江中考)六·一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A,B,C是弯道MN上的三点,矩形ADOG,矩形BEOH,矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数表达式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
解:(1)∵矩形ADOG、矩形BEOH、矩形CFOI的面积相等,∴弯道为反比例函数图象的一部分.设函数表达式为y=(k≠0),OG=GH=HI=a,则AG=,BH=,CI=,所以S2=·a-·a=6,解得k=36,所以S1=·a-·a=k=×36=18,S3=·a=k=×36=12;(2)∵k=36,∴弯道函数表达式为y=.∵T(x,y)是弯道MN上的任一点,∴y=;(3)∵MP=2米,NQ=3米,∴GM==18,=3,解得OQ=12.∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),∴x=2时,y=18,可以种8棵,x=4时,y=9,可以种4棵,x=6时,y=6,可以种2棵,x=8时,y=4.5,可以种2棵,x=10时,y=3.6,可以种1棵.故一共能种植17棵花木.
5
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
