华东师大版九年级数学上册周周清八检测内容24.1-24.3(word版含答案)
文档属性
| 名称 | 华东师大版九年级数学上册周周清八检测内容24.1-24.3(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 12:03:05 | ||
图片预览


文档简介
检测内容:24.1-24.3
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共32分)
1.(南召期末)已知sin
A=,则下列正确的是(
)
A.cos
A=
B.tan
A=1
C.cos
A=
D.tan
A=
2.如图,校园内有两棵树相距12
m,一棵树高13
m,另一棵树高8
m.一只小鸟从一棵树顶飞到另一棵树顶,小鸟至少要飞的路程为(
)
A.13
m
B.12
m
C.8
m
D.以上都不对
3.如图,在△ABC中,D为AB中点,点E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为(
)
A.10
B.11
C.12
D.13
4.化简等于(
)
A.1-
B.-1
C.-1
D.+1
5.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot
A=.则下列关系式中不成立的是(
)
A.tan
A·cot
A=1
B.sin
A=tan
A·cos
A
C.cos
A=cot
A·sin
A
D.tan2A+cot2A=1
6.计算(sin
30°)2-(cos
45°)0+tan
60°·sin
60°的结果是(
)
A.
B.0
C.
D.
7.已知∠A为锐角,且cos
A≤,那么(
)
A.0°B.60°≤A<90°
C.0°D.30°≤A<90°
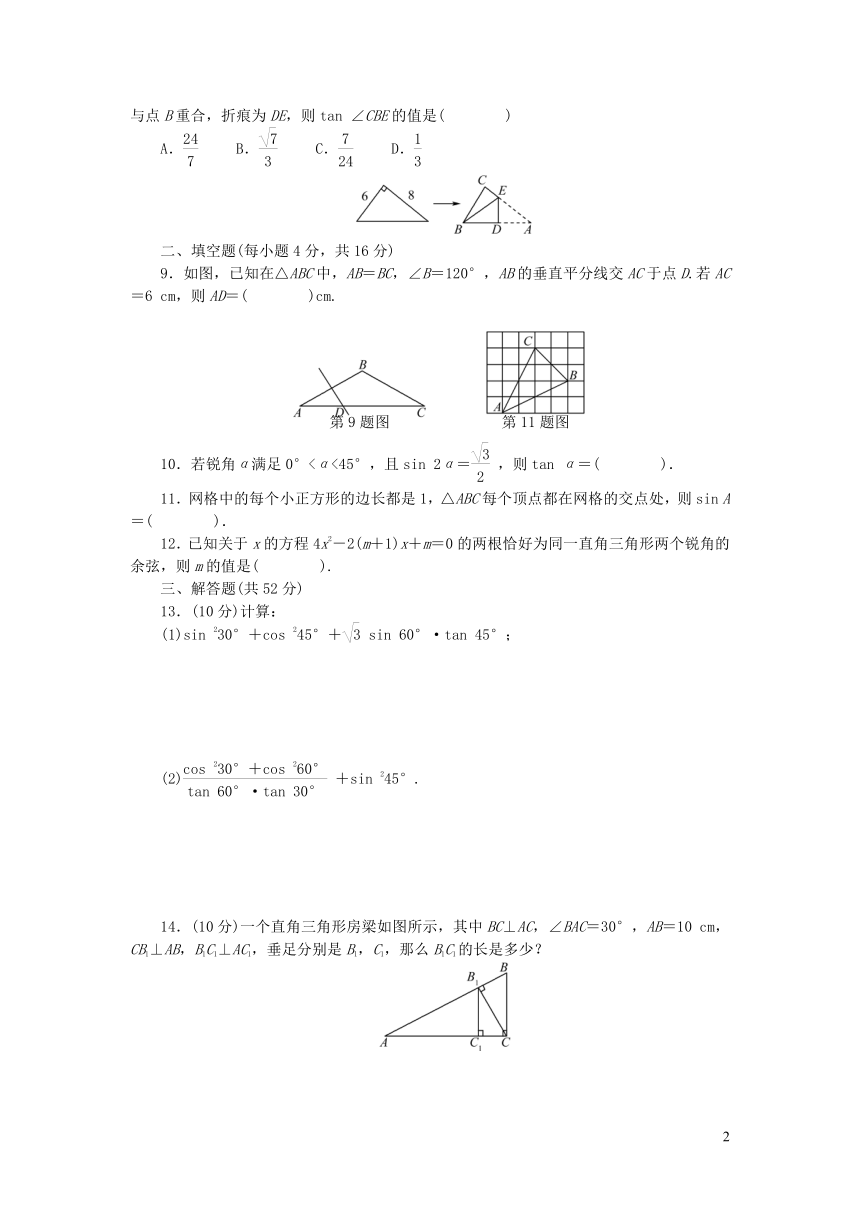
8.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,折痕为DE,则tan
∠CBE的值是(
)
A.
B.
C.
D.
二、填空题(每小题4分,共16分)
9.如图,已知在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6
cm,则AD=(
)cm.
10.若锐角α满足0°<α<45°,且sin
2α=,则tan
α=(
).
11.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sin
A=(
).
12.已知关于x的方程4x2-2(m+1)x+m=0的两根恰好为同一直角三角形两个锐角的余弦,则m的值是(
).
三、解答题(共52分)
13.(10分)计算:
(1)sin
230°+cos
245°+sin
60°·tan
45°;
(2)+sin
245°.
14.(10分)一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,AB=10
cm,CB1⊥AB,B1C1⊥AC1,垂足分别是B1,C1,那么B1C1的长是多少?
15.(10分)如图,在△ABC中,AD是BC上的高,且tan
B=cos
∠DAC.
(1)求证:AC=BD;
(2)若sin
C=,BC=12,求AD的长.
16.(10分)如图,已知AE,BD相交于点C,AC=AD,BC=BE,F,G,H分别是DC,CE,AB的中点.求证:HF=HG.
17.(12分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin
∠DFE=,求tan
∠EBC的值.
检测内容:24.1-24.3(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共32分)
1.(南召期末)已知sin
A=,则下列正确的是(C)
A.cos
A=
B.tan
A=1
C.cos
A=
D.tan
A=
2.如图,校园内有两棵树相距12
m,一棵树高13
m,另一棵树高8
m.一只小鸟从一棵树顶飞到另一棵树顶,小鸟至少要飞的路程为(A)
A.13
m
B.12
m
C.8
m
D.以上都不对
3.如图,在△ABC中,D为AB中点,点E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为(C)
A.10
B.11
C.12
D.13
4.化简等于(A)
A.1-
B.-1
C.-1
D.+1
5.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot
A=.则下列关系式中不成立的是(D)
A.tan
A·cot
A=1
B.sin
A=tan
A·cos
A
C.cos
A=cot
A·sin
A
D.tan2A+cot2A=1
6.计算(sin
30°)2-(cos
45°)0+tan
60°·sin
60°的结果是(C)
A.
B.0
C.
D.
7.已知∠A为锐角,且cos
A≤,那么(B)
A.0°B.60°≤A<90°
C.0°D.30°≤A<90°
8.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,折痕为DE,则tan
∠CBE的值是(C)
A.
B.
C.
D.
二、填空题(每小题4分,共16分)
9.如图,已知在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6
cm,则AD=__2__cm.
10.若锐角α满足0°<α<45°,且sin
2α=,则tan
α=____.
11.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sin
A=____.
12.已知关于x的方程4x2-2(m+1)x+m=0的两根恰好为同一直角三角形两个锐角的余弦,则m的值是____.
三、解答题(共52分)
13.(10分)计算:
(1)sin
230°+cos
245°+sin
60°·tan
45°;
解:
(2)+sin
245°.
解:
14.(10分)一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,AB=10
cm,CB1⊥AB,B1C1⊥AC1,垂足分别是B1,C1,那么B1C1的长是多少?
解:∵BC⊥AC,∠A=30°,AB=10,∴BC=5
cm.∵CB1⊥AB,∠B=90°-∠A=60°,∴∠BCB1=90°-∠B=30°,∴BB1=2.5
cm,∴AB1=AB-BB1=7.5
cm.∵B1C1⊥AC,∠B1AC1=30°,∴B1C1=3.75
cm
15.(10分)如图,在△ABC中,AD是BC上的高,且tan
B=cos
∠DAC.
(1)求证:AC=BD;
(2)若sin
C=,BC=12,求AD的长.
解:(1)略 (2)∵sin
C==,设AD=12k,则AC=13k,由勾股定理得CD=5k,由BC=BD+CD=12,AC=BD,得13k+5k=12,∴k=,∴AD=12k=8
16.(10分)如图,已知AE,BD相交于点C,AC=AD,BC=BE,F,G,H分别是DC,CE,AB的中点.求证:HF=HG.
证明:连结AF,BG.∵AC=AD,BC=BE,∴AF⊥DC,BG⊥EC,∴∠AFB=90°,∠AGB=90°,又∵H为AB的中点,∴FH=AB,GH=AB,∴HF=HG
17.(12分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin
∠DFE=,求tan
∠EBC的值.
解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°.∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°.∴∠AFB+∠DFE=180°-∠BFE=90°.又∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE (2)在Rt△DEF中,sin
∠DFE==,∴设DE=a,EF=3a,则DF==2a.∵△BCE沿BE折叠为△BFE,∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF.又由(1)知△ABF∽△DFE,∴===.∴tan
∠EBF==,即tan
∠EBC=tan
∠EBF=
4
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共32分)
1.(南召期末)已知sin
A=,则下列正确的是(
)
A.cos
A=
B.tan
A=1
C.cos
A=
D.tan
A=
2.如图,校园内有两棵树相距12
m,一棵树高13
m,另一棵树高8
m.一只小鸟从一棵树顶飞到另一棵树顶,小鸟至少要飞的路程为(
)
A.13
m
B.12
m
C.8
m
D.以上都不对
3.如图,在△ABC中,D为AB中点,点E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为(
)
A.10
B.11
C.12
D.13
4.化简等于(
)
A.1-
B.-1
C.-1
D.+1
5.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot
A=.则下列关系式中不成立的是(
)
A.tan
A·cot
A=1
B.sin
A=tan
A·cos
A
C.cos
A=cot
A·sin
A
D.tan2A+cot2A=1
6.计算(sin
30°)2-(cos
45°)0+tan
60°·sin
60°的结果是(
)
A.
B.0
C.
D.
7.已知∠A为锐角,且cos
A≤,那么(
)
A.0°
C.0°
8.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,折痕为DE,则tan
∠CBE的值是(
)
A.
B.
C.
D.
二、填空题(每小题4分,共16分)
9.如图,已知在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6
cm,则AD=(
)cm.
10.若锐角α满足0°<α<45°,且sin
2α=,则tan
α=(
).
11.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sin
A=(
).
12.已知关于x的方程4x2-2(m+1)x+m=0的两根恰好为同一直角三角形两个锐角的余弦,则m的值是(
).
三、解答题(共52分)
13.(10分)计算:
(1)sin
230°+cos
245°+sin
60°·tan
45°;
(2)+sin
245°.
14.(10分)一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,AB=10
cm,CB1⊥AB,B1C1⊥AC1,垂足分别是B1,C1,那么B1C1的长是多少?
15.(10分)如图,在△ABC中,AD是BC上的高,且tan
B=cos
∠DAC.
(1)求证:AC=BD;
(2)若sin
C=,BC=12,求AD的长.
16.(10分)如图,已知AE,BD相交于点C,AC=AD,BC=BE,F,G,H分别是DC,CE,AB的中点.求证:HF=HG.
17.(12分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin
∠DFE=,求tan
∠EBC的值.
检测内容:24.1-24.3(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共32分)
1.(南召期末)已知sin
A=,则下列正确的是(C)
A.cos
A=
B.tan
A=1
C.cos
A=
D.tan
A=
2.如图,校园内有两棵树相距12
m,一棵树高13
m,另一棵树高8
m.一只小鸟从一棵树顶飞到另一棵树顶,小鸟至少要飞的路程为(A)
A.13
m
B.12
m
C.8
m
D.以上都不对
3.如图,在△ABC中,D为AB中点,点E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为(C)
A.10
B.11
C.12
D.13
4.化简等于(A)
A.1-
B.-1
C.-1
D.+1
5.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot
A=.则下列关系式中不成立的是(D)
A.tan
A·cot
A=1
B.sin
A=tan
A·cos
A
C.cos
A=cot
A·sin
A
D.tan2A+cot2A=1
6.计算(sin
30°)2-(cos
45°)0+tan
60°·sin
60°的结果是(C)
A.
B.0
C.
D.
7.已知∠A为锐角,且cos
A≤,那么(B)
A.0°
C.0°
8.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,折痕为DE,则tan
∠CBE的值是(C)
A.
B.
C.
D.
二、填空题(每小题4分,共16分)
9.如图,已知在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6
cm,则AD=__2__cm.
10.若锐角α满足0°<α<45°,且sin
2α=,则tan
α=____.
11.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sin
A=____.
12.已知关于x的方程4x2-2(m+1)x+m=0的两根恰好为同一直角三角形两个锐角的余弦,则m的值是____.
三、解答题(共52分)
13.(10分)计算:
(1)sin
230°+cos
245°+sin
60°·tan
45°;
解:
(2)+sin
245°.
解:
14.(10分)一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,AB=10
cm,CB1⊥AB,B1C1⊥AC1,垂足分别是B1,C1,那么B1C1的长是多少?
解:∵BC⊥AC,∠A=30°,AB=10,∴BC=5
cm.∵CB1⊥AB,∠B=90°-∠A=60°,∴∠BCB1=90°-∠B=30°,∴BB1=2.5
cm,∴AB1=AB-BB1=7.5
cm.∵B1C1⊥AC,∠B1AC1=30°,∴B1C1=3.75
cm
15.(10分)如图,在△ABC中,AD是BC上的高,且tan
B=cos
∠DAC.
(1)求证:AC=BD;
(2)若sin
C=,BC=12,求AD的长.
解:(1)略 (2)∵sin
C==,设AD=12k,则AC=13k,由勾股定理得CD=5k,由BC=BD+CD=12,AC=BD,得13k+5k=12,∴k=,∴AD=12k=8
16.(10分)如图,已知AE,BD相交于点C,AC=AD,BC=BE,F,G,H分别是DC,CE,AB的中点.求证:HF=HG.
证明:连结AF,BG.∵AC=AD,BC=BE,∴AF⊥DC,BG⊥EC,∴∠AFB=90°,∠AGB=90°,又∵H为AB的中点,∴FH=AB,GH=AB,∴HF=HG
17.(12分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin
∠DFE=,求tan
∠EBC的值.
解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°.∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°.∴∠AFB+∠DFE=180°-∠BFE=90°.又∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE (2)在Rt△DEF中,sin
∠DFE==,∴设DE=a,EF=3a,则DF==2a.∵△BCE沿BE折叠为△BFE,∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF.又由(1)知△ABF∽△DFE,∴===.∴tan
∠EBF==,即tan
∠EBC=tan
∠EBF=
4
