北师大版五年级数学上册 6.1 组合图形的面积课件(15张ppt)
文档属性
| 名称 | 北师大版五年级数学上册 6.1 组合图形的面积课件(15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1018.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 20:51:52 | ||
图片预览


文档简介
六 组合图形的面积
1 组合图形的面积
学习目标
1.在探索组合图形面积计算的方法中,体会割补法的应用。
2.能根据组合图形的条件,灵活运用割补法正确计算其面积。
3.能解决生活中与组合图形有关的实际问题,认识数学的价值。
重点
能根据组合图形的条件,灵活运用割补法正确计算其面积。
难点
能解决生活中与组合图形有关的实际问题。
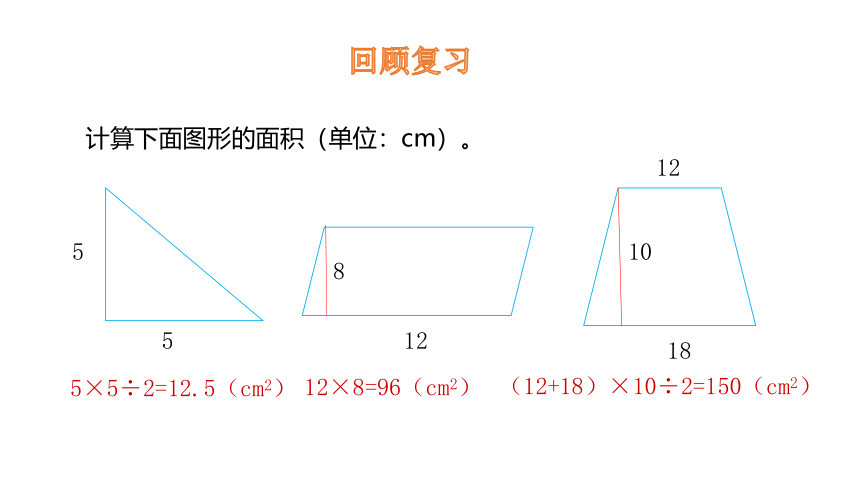
回顾复习
计算下面图形的面积(单位:cm)。
5
5
12
8
18
10
12
5×5÷2=12.5(cm2)
12×8=96(cm2)
(12+18)×10÷2=150(cm2)
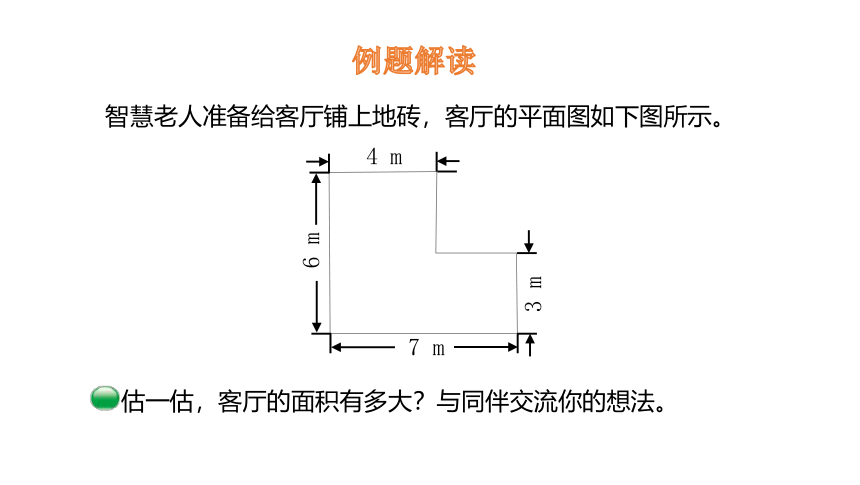
例题解读
估一估,客厅的面积有多大?与同伴交流你的想法。
智慧老人准备给客厅铺上地砖,客厅的平面图如下图所示。
7 m
4 m
6 m
3 m
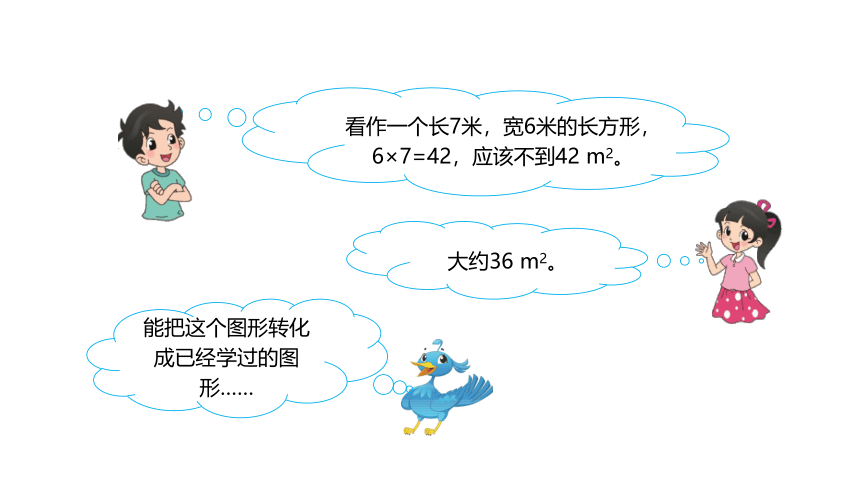
看作一个长7米,宽6米的长方形,6×7=42,应该不到42 m2。
大约36 m2。
能把这个图形转化成已经学过的图形……
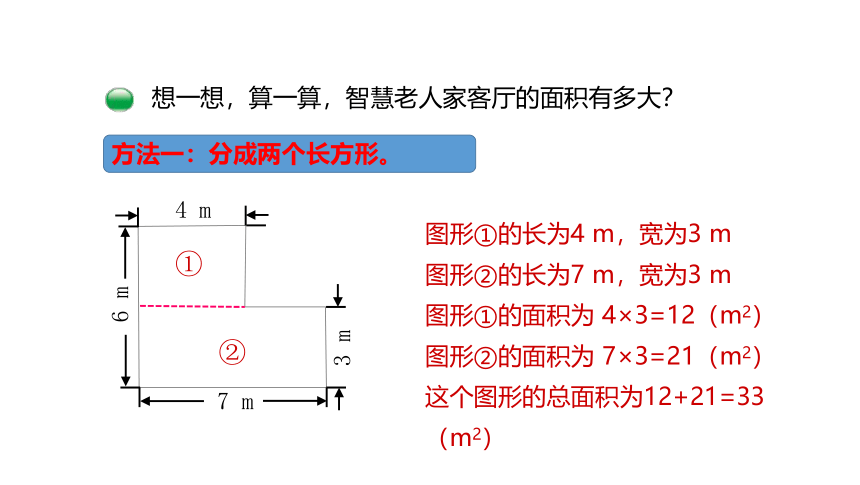
想一想,算一算,智慧老人家客厅的面积有多大?
方法一:分成两个长方形。
7 m
4 m
6 m
3 m
①
②
图形①的长为4 m,宽为3 m
图形②的长为7 m,宽为3 m
图形①的面积为 4×3=12(m2)
图形②的面积为 7×3=21(m2)
这个图形的总面积为12+21=33(m2)
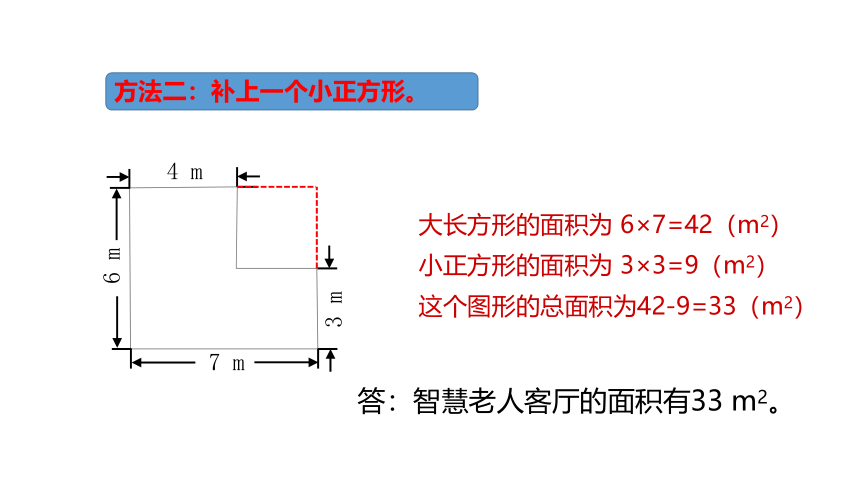
方法二:补上一个小正方形。
7 m
4 m
6 m
3 m
大长方形的面积为 6×7=42(m2)
小正方形的面积为 3×3=9(m2)
这个图形的总面积为42-9=33(m2)
答:智慧老人客厅的面积有33 m2。
还有其他方法计算客厅的面积吗?试一试,与同伴交流。
7 m
4 m
6 m
3 m
①
②
图形①的长为6 m,宽为4 m
图形②的长为3 m,宽为3 m
图形①的面积为 6×4=24(m2)
图形②的面积为 3×3=9(m2)
这个图形的总面积为24+9=33(m2)
7 m
4 m
6 m
3 m
图形①的面积为
(3+6)×4÷2=18(m2)
图形②的面积为
(3+7)×3÷2=15(m2)
这个图形的总面积为18+15=33(m2)
①
②
典型例题
【例1】右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
分成一个三角形和一个正方形
三角形面积=5×2÷2=5(m2)
正方形面积=5×5=25(m2)
房子侧面墙面积=25+5 =30(m2)
【例2】一个指示牌的形状是一个组合图形,求它的面积。
20×10
+ 20×10÷2
= 300(cm2)
小结
求组合图形面积的方法
(1)观察、分析组合图形可分割或添补哪些学过的基本图形。
(2)找出计算基本图形面积需要的条件,然后利用合理的方
法,计算出基本图形的面积。
(3)利用基本图形的面积和或差计算出组合图形的面积。
随堂小测
1.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2
- 3×4÷2
- (4+6)×4÷2
= 46(cm2)
2.为举办秋季体育节,学校制作了锦旗(如下图),一面锦旗需要多少平方厘米布料?
30×60-30×(60-45)÷2=1575(平方厘米)
答:一面锦旗需要1575平方厘米布料。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1 组合图形的面积
学习目标
1.在探索组合图形面积计算的方法中,体会割补法的应用。
2.能根据组合图形的条件,灵活运用割补法正确计算其面积。
3.能解决生活中与组合图形有关的实际问题,认识数学的价值。
重点
能根据组合图形的条件,灵活运用割补法正确计算其面积。
难点
能解决生活中与组合图形有关的实际问题。
回顾复习
计算下面图形的面积(单位:cm)。
5
5
12
8
18
10
12
5×5÷2=12.5(cm2)
12×8=96(cm2)
(12+18)×10÷2=150(cm2)
例题解读
估一估,客厅的面积有多大?与同伴交流你的想法。
智慧老人准备给客厅铺上地砖,客厅的平面图如下图所示。
7 m
4 m
6 m
3 m
看作一个长7米,宽6米的长方形,6×7=42,应该不到42 m2。
大约36 m2。
能把这个图形转化成已经学过的图形……
想一想,算一算,智慧老人家客厅的面积有多大?
方法一:分成两个长方形。
7 m
4 m
6 m
3 m
①
②
图形①的长为4 m,宽为3 m
图形②的长为7 m,宽为3 m
图形①的面积为 4×3=12(m2)
图形②的面积为 7×3=21(m2)
这个图形的总面积为12+21=33(m2)
方法二:补上一个小正方形。
7 m
4 m
6 m
3 m
大长方形的面积为 6×7=42(m2)
小正方形的面积为 3×3=9(m2)
这个图形的总面积为42-9=33(m2)
答:智慧老人客厅的面积有33 m2。
还有其他方法计算客厅的面积吗?试一试,与同伴交流。
7 m
4 m
6 m
3 m
①
②
图形①的长为6 m,宽为4 m
图形②的长为3 m,宽为3 m
图形①的面积为 6×4=24(m2)
图形②的面积为 3×3=9(m2)
这个图形的总面积为24+9=33(m2)
7 m
4 m
6 m
3 m
图形①的面积为
(3+6)×4÷2=18(m2)
图形②的面积为
(3+7)×3÷2=15(m2)
这个图形的总面积为18+15=33(m2)
①
②
典型例题
【例1】右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
分成一个三角形和一个正方形
三角形面积=5×2÷2=5(m2)
正方形面积=5×5=25(m2)
房子侧面墙面积=25+5 =30(m2)
【例2】一个指示牌的形状是一个组合图形,求它的面积。
20×10
+ 20×10÷2
= 300(cm2)
小结
求组合图形面积的方法
(1)观察、分析组合图形可分割或添补哪些学过的基本图形。
(2)找出计算基本图形面积需要的条件,然后利用合理的方
法,计算出基本图形的面积。
(3)利用基本图形的面积和或差计算出组合图形的面积。
随堂小测
1.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2
- 3×4÷2
- (4+6)×4÷2
= 46(cm2)
2.为举办秋季体育节,学校制作了锦旗(如下图),一面锦旗需要多少平方厘米布料?
30×60-30×(60-45)÷2=1575(平方厘米)
答:一面锦旗需要1575平方厘米布料。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
