北师大版六年级数学上册 数学好玩 第3课时 比赛场次课件(19张ppt)
文档属性
| 名称 | 北师大版六年级数学上册 数学好玩 第3课时 比赛场次课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 20:38:33 | ||
图片预览





文档简介
第3课时 比赛场次
数学好玩
学习目标
结合体育中的实例,探索比赛中的搭配问题,会用列表、画图的方式寻找实际问题中蕴含的简单的规律,体会图表的简洁性和有效性。
在解决问题的过程中,了解“从简单的情形开始寻找规律”的解决问题的策略,提高解决问题的能力,培养探究能力,发展数学思维。
4个女生和2个男生进行羽毛球单打比赛,如果每个女同学和每个男同学分别打一场,一共要打多少场?
8场
回顾复习
世界杯比赛场次
8组:A B C D E F G H
32支球队
每组4队
(单循环赛)
9
10
11
12
1
2
3
4
5
6
7
8
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
获胜后的队(淘汰赛)
16支队伍
名两前
8支队伍
冠军
4强
争夺冠军、亚军、季军
情境引入
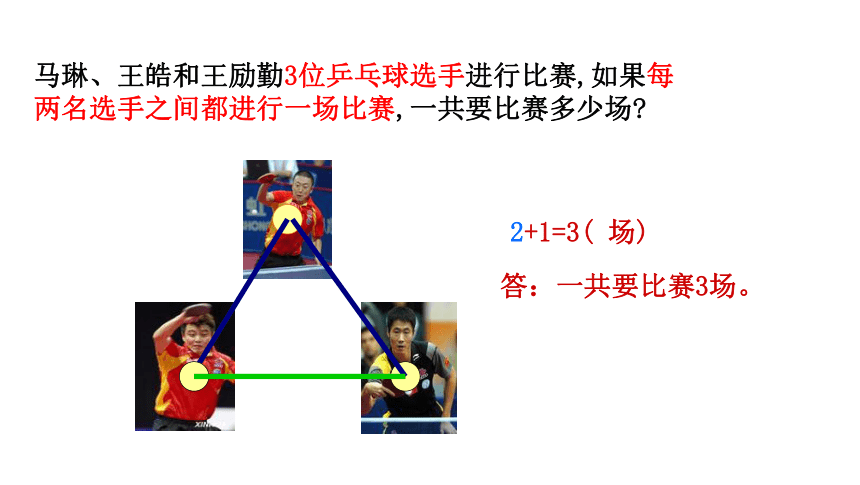
马琳、王皓和王励勤3位乒乓球选手进行比赛,如果每两名选手之间都进行一场比赛,一共要比赛多少场?
2+1=3( 场)
答:一共要比赛3场。
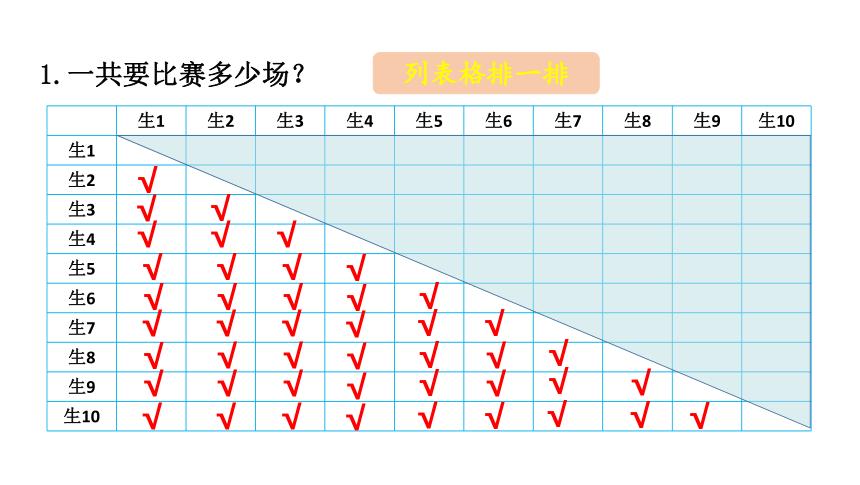
六⑴班10名同学进行乒乓球比赛,每两名同学之间要进行一场比赛。
乒乓球比赛
例题解读
1.一共要比赛多少场?
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
列表格排一排
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
画图数一数
1.一共要比赛多少场?
1
1
1+2=3
3
1+2+3=6
6
1+2+3+4=10
10
2.从简单情形入手找规律。
方案一:画表格
2.从简单情形入手找规律。
方案二:画图
2
3
4
5
1
1
1+2=3
3
1+2+3=6
6
1+2+3+4=10
10
{616DA210-FB5B-4158-B5E0-FEB733F419BA}比赛人数
示意图
各点之间连线数
比赛场次
2
1
3
1+2=3
4
1+2+3=6
5
1+2+3+4=10
1
3
6
10
2.从简单情形入手找规律。
方案三:连线
{5940675A-B579-460E-94D1-54222C63F5DA}比赛人数
比赛场数
3.现在你知道一共要比赛多少场了吗?
2
1
3
1+2=3
4
1+2+3=6
5
1+2+3+4=10
6
1+2+3+4+5=15
7
1+2+3+4+5+6=21
8
1+2+3+4+5+6+7=28
9
1+2+3+4+5+6+7+8=36
10
1+2+3+4+5+6+7+8+9=45
教练
队长1
队长2
同学
同学
同学
同学
1分
1分
联络方式
星星体操表演队为联络方便,设计了一种联络方式。一旦有事,先由教练同时通知两位队长,两位队长再分别同时通知两名同学,依此类推,每人再同时通知两个人。每同时通知两人共需1分。
例题解读
{5940675A-B579-460E-94D1-54222C63F5DA}时间/分
通知到的同学数
1
2
2
2+4=6
3
2+4+8=14
4
2+4+8+16=30
5
2+4+8+16+32=62
联络方式
2.(1)你发现了什么规律?
第n分钟通知到的学生数比前(n-1)分通知到的同学数的2倍还多2人。
联络方式
(2)如果有126名同学,需要多长时间通知完?
第6分钟通知的人数共是2+4+8+16+32+64=126(人)
第6分钟可以通知62×2+2=126(人)
3.你能为我们班设计一种联络方式吗?请你用图表示出来。
班长
组长1
组长2
组员1
组员2
组员3
组员4
班副
组长3
组长4
组员5
组员6
组员7
组员8
老师
组员9
组员10
组员11
组员12
组员13
组员14
组员15
组员16
……
联络方式
少年宫“春苗杯”围棋赛有13名同学参加,如果每两名选手都进
行一场比赛,一共要比赛多少场?
1+2+3+4+5+6+7+8+9+10+11+12
=78(场)
答:一共要比赛78场。
随堂小测
2. 从A地到B地,中间有10个车站(不包括A,B站),铁道部门共要准备多少种车票?
(1+2+3+4+5+6+7+8+9+10+11)
×2
=132(种)
答:铁道部门共要准备132种车票。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
数学好玩
学习目标
结合体育中的实例,探索比赛中的搭配问题,会用列表、画图的方式寻找实际问题中蕴含的简单的规律,体会图表的简洁性和有效性。
在解决问题的过程中,了解“从简单的情形开始寻找规律”的解决问题的策略,提高解决问题的能力,培养探究能力,发展数学思维。
4个女生和2个男生进行羽毛球单打比赛,如果每个女同学和每个男同学分别打一场,一共要打多少场?
8场
回顾复习
世界杯比赛场次
8组:A B C D E F G H
32支球队
每组4队
(单循环赛)
9
10
11
12
1
2
3
4
5
6
7
8
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
获胜后的队(淘汰赛)
16支队伍
名两前
8支队伍
冠军
4强
争夺冠军、亚军、季军
情境引入
马琳、王皓和王励勤3位乒乓球选手进行比赛,如果每两名选手之间都进行一场比赛,一共要比赛多少场?
2+1=3( 场)
答:一共要比赛3场。
六⑴班10名同学进行乒乓球比赛,每两名同学之间要进行一场比赛。
乒乓球比赛
例题解读
1.一共要比赛多少场?
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
列表格排一排
生1
生2
生3
生4
生5
生6
生7
生8
生9
生10
画图数一数
1.一共要比赛多少场?
1
1
1+2=3
3
1+2+3=6
6
1+2+3+4=10
10
2.从简单情形入手找规律。
方案一:画表格
2.从简单情形入手找规律。
方案二:画图
2
3
4
5
1
1
1+2=3
3
1+2+3=6
6
1+2+3+4=10
10
{616DA210-FB5B-4158-B5E0-FEB733F419BA}比赛人数
示意图
各点之间连线数
比赛场次
2
1
3
1+2=3
4
1+2+3=6
5
1+2+3+4=10
1
3
6
10
2.从简单情形入手找规律。
方案三:连线
{5940675A-B579-460E-94D1-54222C63F5DA}比赛人数
比赛场数
3.现在你知道一共要比赛多少场了吗?
2
1
3
1+2=3
4
1+2+3=6
5
1+2+3+4=10
6
1+2+3+4+5=15
7
1+2+3+4+5+6=21
8
1+2+3+4+5+6+7=28
9
1+2+3+4+5+6+7+8=36
10
1+2+3+4+5+6+7+8+9=45
教练
队长1
队长2
同学
同学
同学
同学
1分
1分
联络方式
星星体操表演队为联络方便,设计了一种联络方式。一旦有事,先由教练同时通知两位队长,两位队长再分别同时通知两名同学,依此类推,每人再同时通知两个人。每同时通知两人共需1分。
例题解读
{5940675A-B579-460E-94D1-54222C63F5DA}时间/分
通知到的同学数
1
2
2
2+4=6
3
2+4+8=14
4
2+4+8+16=30
5
2+4+8+16+32=62
联络方式
2.(1)你发现了什么规律?
第n分钟通知到的学生数比前(n-1)分通知到的同学数的2倍还多2人。
联络方式
(2)如果有126名同学,需要多长时间通知完?
第6分钟通知的人数共是2+4+8+16+32+64=126(人)
第6分钟可以通知62×2+2=126(人)
3.你能为我们班设计一种联络方式吗?请你用图表示出来。
班长
组长1
组长2
组员1
组员2
组员3
组员4
班副
组长3
组长4
组员5
组员6
组员7
组员8
老师
组员9
组员10
组员11
组员12
组员13
组员14
组员15
组员16
……
联络方式
少年宫“春苗杯”围棋赛有13名同学参加,如果每两名选手都进
行一场比赛,一共要比赛多少场?
1+2+3+4+5+6+7+8+9+10+11+12
=78(场)
答:一共要比赛78场。
随堂小测
2. 从A地到B地,中间有10个车站(不包括A,B站),铁道部门共要准备多少种车票?
(1+2+3+4+5+6+7+8+9+10+11)
×2
=132(种)
答:铁道部门共要准备132种车票。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
