人教新课标数学六年级下册《圆柱的表面积 6》ppt课件
文档属性
| 名称 | 人教新课标数学六年级下册《圆柱的表面积 6》ppt课件 |  | |
| 格式 | rar | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-27 14:50:38 | ||
图片预览






文档简介
(共21张PPT)
人教新课标六年级数学下册
圆柱的表面积
1.使同学们理解和掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
2.培养同学们观察、比较、分析、推理的能力,并会根据实际问题灵活解答。
一、引入
1.圆的面积计算公式:
S = πr2
2.圆的周长计算公式:
C = πd
C = 2πr
r
S = ab
3.长方形面积计算公式:
a
b
练习一:求下列圆柱的侧面积
(1)底面周长为18厘米,高为10厘米。
(2)底面直径为10厘米,高为15厘米。
(3)底面半径为6厘米,高为10厘米。
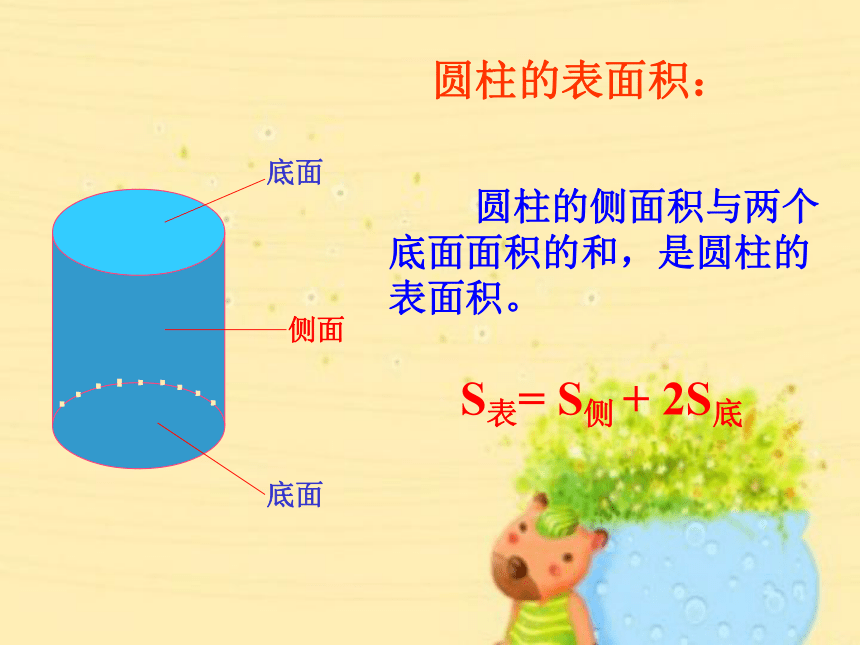
底面
底面
侧面
圆柱的侧面积与两个底面面积的和,是圆柱的表面积。
圆柱的表面积:
S表= S侧 + 2S底
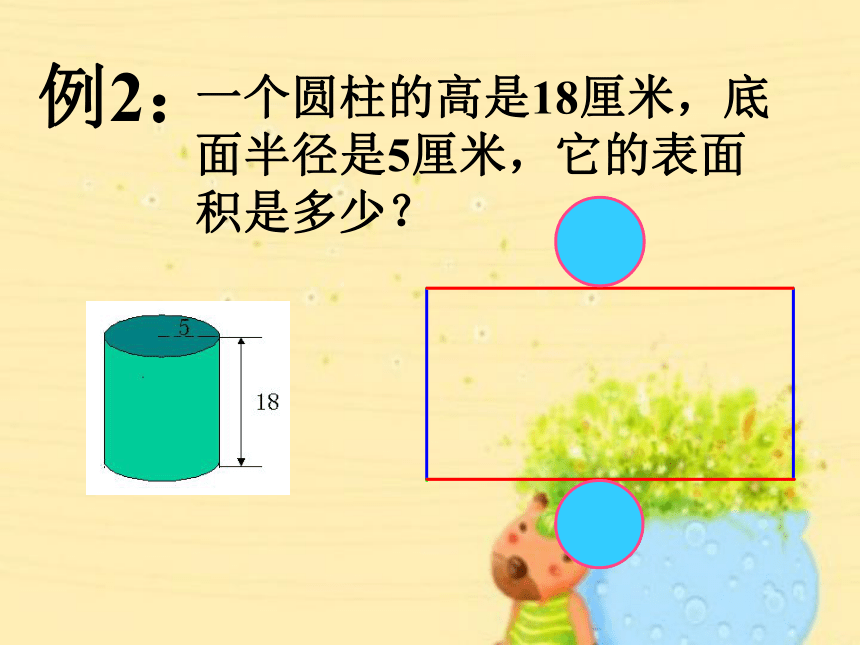
例2:
一个圆柱的高是18厘米,底面半径是5厘米,它的表面积是多少?
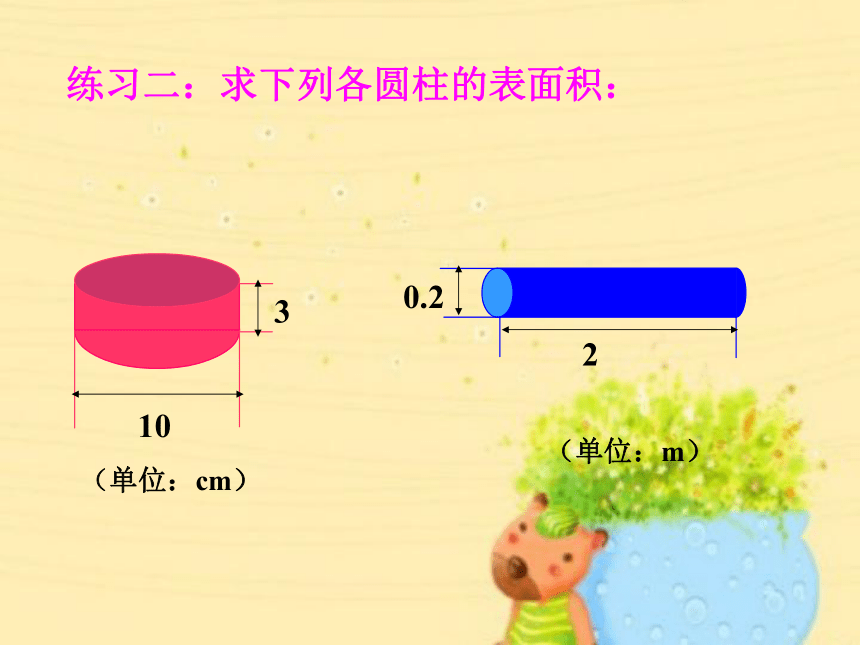
练习二:求下列各圆柱的表面积:
2
0.2
10
3
(单位:cm)
(单位:m)
练习三
例题3
小结
操作
判断
选择
思考
小结
练习三:
(一)操作:
剪长方形、平行四边形、梯形的纸各一张,试一试哪些纸能围成圆柱形的纸筒。
能
能
不能
用一张边长2分米的正方形纸围成一个圆柱形的纸筒,它的侧面积是多少?
2
2
答:4平方分米
控制
(二)判断:
1. 上下两个底面是圆形的物体都是圆柱。 ( )
2. 圆柱的表面积是圆柱的底面积加上侧面积。( )
3. 圆柱底面半径不变,高扩大2倍,侧面积也扩大2倍。( )
控制
(三)选择:
1.有一个圆柱底面半径是10cm,高是20cm,求表面积的算式是( )。
A 2×3.14×10×20
B 3.14×102
C 2×3.14×10×20+2×3.14×102
D 2×3.14×10×20+3.14×102
C
2.如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2。
A 12
B 18
C 24
D 36
C
小结
控制
操作
思考
返回
(四)思考: 一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1. 以20π厘米为底面周长,10 π厘米为高。
2. 以10 π厘米为底面周长 ,20 π厘米为高。
20 π
10π
10 π
20π
小结
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以20π厘米为底面周长,10 π厘米为高。
解:C=20 π厘米,
h=10 π厘米
S侧=Ch
=20 π×10 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=10(cm)
S底= πr2=100 π(cm2)
S表=S侧+2S底=(200 π2+200 π )cm2
20π
10π
答:这个圆柱的表面积为(200π2+200π)cm2或(200π2+50π)cm2
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以10π厘米为底面周长,20 π厘米为高。
解:C=10 π厘米,
h=20 π厘米
S侧=Ch
=10 π×20 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=5(cm)
S底= πr2=25 π(cm2)
S表=S侧+2S底=(200 π2+50 π )cm2
10π
20π
小结
控制
10
S侧=3.14 × 6 × 10=188.4(cm2)
下面两个圆柱体的侧面积、表面积是否相等?(单位:厘米)
10
6
6
S底=3.14 × (6/2)2=28.26(cm2)
S表=S侧+2S底=244.92(cm2)
S侧=3.14 × 10 × 6=188.4(cm2)
S底=3.14 × (10/2)2=78.5(cm2)
S表=S侧+2S底=345.4(cm2)
两个圆柱的侧面积相等,表面积不相等。
小结
例3:一个没有盖的圆柱形铁皮水桶,高是48厘米,底面直径是30厘米,做这个水桶至少要用铁皮多少平方厘米?(得数保留整百平方厘米)。
控制页
(1)水桶的侧面积:
3.14 ×30 ×48=4521.6(平方厘米)
(2)水桶的底面积:
3.14 ×(30/2) 2 =3.14 ×15 2 =3.14 ×225=706.5(平方厘米)
(3)需要铁皮:
4521.6+706.5=5228.1≈5300(平方厘米)
小结:
1. 这节课我们 学习了哪些知识?
2. 圆柱的表面积计算公式:
S表 = S侧 + 2S底
3. 在日常生活中,我们可以利用圆柱的侧面积计算公式和表面积计算公式,解决哪些问题?
控制页
人教新课标六年级数学下册
圆柱的表面积
1.使同学们理解和掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
2.培养同学们观察、比较、分析、推理的能力,并会根据实际问题灵活解答。
一、引入
1.圆的面积计算公式:
S = πr2
2.圆的周长计算公式:
C = πd
C = 2πr
r
S = ab
3.长方形面积计算公式:
a
b
练习一:求下列圆柱的侧面积
(1)底面周长为18厘米,高为10厘米。
(2)底面直径为10厘米,高为15厘米。
(3)底面半径为6厘米,高为10厘米。
底面
底面
侧面
圆柱的侧面积与两个底面面积的和,是圆柱的表面积。
圆柱的表面积:
S表= S侧 + 2S底
例2:
一个圆柱的高是18厘米,底面半径是5厘米,它的表面积是多少?
练习二:求下列各圆柱的表面积:
2
0.2
10
3
(单位:cm)
(单位:m)
练习三
例题3
小结
操作
判断
选择
思考
小结
练习三:
(一)操作:
剪长方形、平行四边形、梯形的纸各一张,试一试哪些纸能围成圆柱形的纸筒。
能
能
不能
用一张边长2分米的正方形纸围成一个圆柱形的纸筒,它的侧面积是多少?
2
2
答:4平方分米
控制
(二)判断:
1. 上下两个底面是圆形的物体都是圆柱。 ( )
2. 圆柱的表面积是圆柱的底面积加上侧面积。( )
3. 圆柱底面半径不变,高扩大2倍,侧面积也扩大2倍。( )
控制
(三)选择:
1.有一个圆柱底面半径是10cm,高是20cm,求表面积的算式是( )。
A 2×3.14×10×20
B 3.14×102
C 2×3.14×10×20+2×3.14×102
D 2×3.14×10×20+3.14×102
C
2.如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2。
A 12
B 18
C 24
D 36
C
小结
控制
操作
思考
返回
(四)思考: 一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1. 以20π厘米为底面周长,10 π厘米为高。
2. 以10 π厘米为底面周长 ,20 π厘米为高。
20 π
10π
10 π
20π
小结
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以20π厘米为底面周长,10 π厘米为高。
解:C=20 π厘米,
h=10 π厘米
S侧=Ch
=20 π×10 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=10(cm)
S底= πr2=100 π(cm2)
S表=S侧+2S底=(200 π2+200 π )cm2
20π
10π
答:这个圆柱的表面积为(200π2+200π)cm2或(200π2+50π)cm2
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以10π厘米为底面周长,20 π厘米为高。
解:C=10 π厘米,
h=20 π厘米
S侧=Ch
=10 π×20 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=5(cm)
S底= πr2=25 π(cm2)
S表=S侧+2S底=(200 π2+50 π )cm2
10π
20π
小结
控制
10
S侧=3.14 × 6 × 10=188.4(cm2)
下面两个圆柱体的侧面积、表面积是否相等?(单位:厘米)
10
6
6
S底=3.14 × (6/2)2=28.26(cm2)
S表=S侧+2S底=244.92(cm2)
S侧=3.14 × 10 × 6=188.4(cm2)
S底=3.14 × (10/2)2=78.5(cm2)
S表=S侧+2S底=345.4(cm2)
两个圆柱的侧面积相等,表面积不相等。
小结
例3:一个没有盖的圆柱形铁皮水桶,高是48厘米,底面直径是30厘米,做这个水桶至少要用铁皮多少平方厘米?(得数保留整百平方厘米)。
控制页
(1)水桶的侧面积:
3.14 ×30 ×48=4521.6(平方厘米)
(2)水桶的底面积:
3.14 ×(30/2) 2 =3.14 ×15 2 =3.14 ×225=706.5(平方厘米)
(3)需要铁皮:
4521.6+706.5=5228.1≈5300(平方厘米)
小结:
1. 这节课我们 学习了哪些知识?
2. 圆柱的表面积计算公式:
S表 = S侧 + 2S底
3. 在日常生活中,我们可以利用圆柱的侧面积计算公式和表面积计算公式,解决哪些问题?
控制页
