人教版新教材高中数学第一册1.1集合的概念(共28张PPT)
文档属性
| 名称 | 人教版新教材高中数学第一册1.1集合的概念(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 879.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 16:09:03 | ||
图片预览








文档简介
(共28张PPT)
1.1
集合的概念
新高考新教材
高中数第一册第一章集合与常用逻辑用语
情景1:“集合”是日常生活中的一个常用词,现代汉语
解释为:许多的人或物聚在一起.
在现代数学中,集合是一种简洁、高雅的数学语言,我们怎样理解数学中的“集合”?
康托尔(G.Cantor,1845-1918).德国数学家,集合论创始人.人们把康托尔于1873年12月7日给戴德金的信中最早提出集合论思想的那一天定为集合论诞生日.
情景导学
看下面几个例子,概括它们有何共同特点?
(1)1-10以内所有的偶数.
(2)立德中学今年入学的全体高一学生.
(3)所有的正方形;
(4)到直线l距离等于定长d的所有点;
(5)方程
x2
-3x+2=0的所有实数根
(6)地球上的四大洋
探究1
:元素与集合的概念
问题探究
一般地,
我们把研究对象统称为元素(element).
通常用小写拉丁字母a,b,c,...来表示.
我们把一些元素组成的总体叫做集合(set)(简称为集).
通常用大写拉丁字母A,B,C,...来表示.
组成集合的元素一定是数吗?
组成集合的元素可以是物、数、图、人等,它具备怎样的性质呢?
问题:
归纳总结
1.
所有的“帅哥”能否构成一个集合?由此说明什么?
集合中的元素是确定的
探究2:
集合中元素的性质
问题探究
“帅”是一个含糊不清的概念,具有相对性,多么“帅”才算“帅”?没有明确的标准,也就是说,是一些不能够确定的对象.因此,不能构成集合.
不能.
其中的元素不确定
2.
由1,3,0,5,︱-3
︳这些数组成的一个集合中有5
个
元素,这种说法正确吗?
集合中的元素是互异的
问题探究
不正确.集合中只有4个不同元素1,3,0,5
.
3.高一(5)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
集合中的元素是没有顺序的
通过以上的学习你能给出集合中元素的特性吗?
确定性、互异性、无序性
问题探究
集合没有变化
只要构成两个集合的元素是一样,我们就称
这两个集合是相等的。
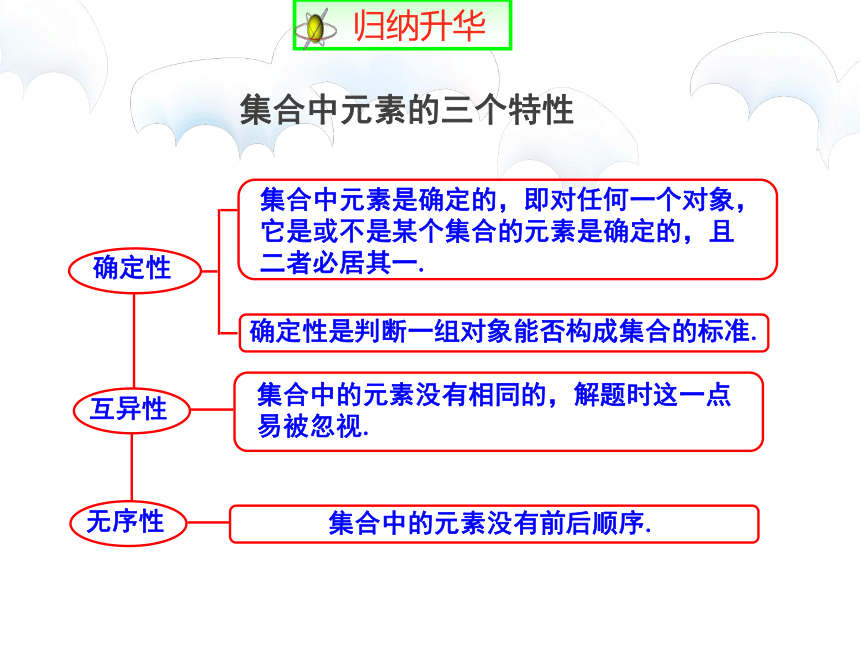
集合中元素的三个特性
集合中元素是确定的,即对任何一个对象,
它是或不是某个集合的元素是确定的,且
二者必居其一.
确定性是判断一组对象能否构成集合的标准.
确定性
互异性
无序性
集合中的元素没有相同的,解题时这一点
易被忽视.
集合中的元素没有前后顺序.
归纳升华
启示:任何集合的元素都不能违背确定性、互异性、无序性.我们还可以用这些性质继续去探求集合与元素的关系.
1.判断以下元素的全体是否组成集合,并说明理由:
(1)
大于3小于11的偶数;
(2)
我国的小河流.
【提示】(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
学以致用
3.已知下面的两个实例:
(1)用A表示高一(8)班全体学生组成的集合.
(2)用a表示高一(8)班的一位同学,b表示高一(7)
班的一位同学.
a是集合A中的元素,
b不是集合A中的元素.
探究3:
元素和集合的关系
问题探究
思考:那么a,b与集合A分别有什么关系?
元素a与集合A的关系
如果a是集合A的元素,就说
a
属于集合A,
记作:a∈A
;
如果a不是集合A中的元素,就说
a
不属于集合A,
记作:a
?
A.
归纳总结
常用的数集
自然数集
正整数集
整数集
有理数集
实数集
记法
——
————
——
——
——
N
Z
Q
R
N
或N+
N
N
或N+
Z
N
或N+
学习集合与元素的概念后,为了方便书写,数学中规定了一些常用数集及其记法:
归纳总结
例2
用符号“∈”或“?”填空.
(1)2
N.
(2)
____________Q.
(3)0
{0}.
(4)b
{a,b,c}.
【总结提升】求解此类问题必须要做到以下两点:
①熟记常见的数集的符号;
②正确理解元素与集合之间的“属于”关系.
问题思考
“地球上的四大洋”组成集合可以表示为:
{太平洋,大西洋,印度洋,北冰洋}.
“方程x2-3x+2=0的所有实数根”,可以表示:
{1,2}
集合的表示方法
像这样把集合的元素一一列举出来,并用花
括号“{
}”括起来表示集合的方法叫做列举法.
集合的元素用“,”号分开.
用列举法表示下列集合:
(1)小于10的所有的自然数组成的集合;
(2)方程
x
2=x
的解;
(1)大括号不能缺失.
(2)有些集合元素个数较多,元素又呈现出一定的规律,在不至于发生误解的情况下,亦可如下表示:从1到100的所有整数组成的集合:{1,2,3,…,100}
自然数集N:{1,2,3,4,…,n,…}
(3)区分a与{a}:{a}表示一个集合,该集合只有一个元素.a表示这个集合的一个元素.
(4)用列举法表示集合时不必考虑元素的前后次序.相同的元素不能出现两次.
注意
用列举法表示出集合:{(1,2),(2,3)}
表示是什么样集合?
所有的集合都可以用列表法来表示吗?比如:不等式x-7<3的解集能用列举法吗?为什么?那么怎样来表示这个集合呢?
这个集合中的元素是列举不完的,可以用集合所含元素的共同特征表示集合.
集合的表示方法三:
不等式x-7<3的解是x<10,有无数个集,我们可以用解集中元素的共同特征,把解集表示:
整数集Z可以分为奇数集和偶数集,利用奇数的特征表示所有奇数:
用利用偶数的特征,表示所有偶数:
实数集R中,有限小数和无限循环小数都可以表示成分数形式,
则有理数集可以表示
描述法:用确定的条件表示某些对象是否属于这个集合的方法.
具体方法:
在花括号内先写上表示这个集合元素的一般符号及取值范围,在画一条竖线,在竖线后写出这个集合中的元素所具有的共同特征.
{x|
P(x)}或{x∈A|
P(x)}
含义:在集合A中满足条件P(x)的x的集合.
集合的表示方法三:
1.使用描述法表示下列集合:
(1)
不等式2x-1>3的解集A;
(2)由大于10且小于20的所有整数组成的集合B
(3)方程
x2
-2=0
的所有实数根组成的集合;
(4)方程组
的解集.
做一做
{(3.5,-1.5)}
2.方程组
的解集用列举法表示为
__________________________
;
用描述法表示为______________________.
用列举法表示为
{(0,6),(1,5),(2,4),(3,3),(6,0),(5,1),(4,2)}
?
有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法.
有些集合的元素不能无遗漏地一一列举出来,或者不便于、不需要一一列举出来,常用描述法.
何时用列举法,何时
用描述法更容易一
些呢?
集合的表示方法四:
韦恩图:用一条封闭的曲线的内部来表示一个集合.
有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法.
集合A
集合B
1.已知集合A含有三个元素a+2,(a+1)2,a2+3a+3,若1∈A,求实数a的值.
【解析】因为1∈A,所以
①若a+2=1,解得a=-1,此时集合含有1,0,1三个元素,元素重复,所以不成立,即a≠-1.
②若(a+1)2=1,解得a=0或a=-2,当a=0时,集合A含有2,1,3三个元素,满足条件,即a=0成立.
典型题一:元素的互异性典型题一:元素的互异性
当a=-2时,集合A含有0,1,1三个元素,
元素重复,所以不成立,即a≠-2.
③
若a2+3a+3=1,解得a=-1或a=-2,由①②知都
不成立.
所以满足条件的实数a的取值为0,即a=0.
典型题一:元素的互异性典型题一:元素的互异性
(2)若{1,
2,a2-1}={1,a2-a,0},则
a=_________.
(3)若{1,2}={a-2,2h},则求
a,
h?
1.集合
与集合
是同一集合吗?
答:不是.集合
是点集,集合
是数集.
典型题二:描述法典型题二:描述法
课堂小结
1.1
集合的概念
新高考新教材
高中数第一册第一章集合与常用逻辑用语
情景1:“集合”是日常生活中的一个常用词,现代汉语
解释为:许多的人或物聚在一起.
在现代数学中,集合是一种简洁、高雅的数学语言,我们怎样理解数学中的“集合”?
康托尔(G.Cantor,1845-1918).德国数学家,集合论创始人.人们把康托尔于1873年12月7日给戴德金的信中最早提出集合论思想的那一天定为集合论诞生日.
情景导学
看下面几个例子,概括它们有何共同特点?
(1)1-10以内所有的偶数.
(2)立德中学今年入学的全体高一学生.
(3)所有的正方形;
(4)到直线l距离等于定长d的所有点;
(5)方程
x2
-3x+2=0的所有实数根
(6)地球上的四大洋
探究1
:元素与集合的概念
问题探究
一般地,
我们把研究对象统称为元素(element).
通常用小写拉丁字母a,b,c,...来表示.
我们把一些元素组成的总体叫做集合(set)(简称为集).
通常用大写拉丁字母A,B,C,...来表示.
组成集合的元素一定是数吗?
组成集合的元素可以是物、数、图、人等,它具备怎样的性质呢?
问题:
归纳总结
1.
所有的“帅哥”能否构成一个集合?由此说明什么?
集合中的元素是确定的
探究2:
集合中元素的性质
问题探究
“帅”是一个含糊不清的概念,具有相对性,多么“帅”才算“帅”?没有明确的标准,也就是说,是一些不能够确定的对象.因此,不能构成集合.
不能.
其中的元素不确定
2.
由1,3,0,5,︱-3
︳这些数组成的一个集合中有5
个
元素,这种说法正确吗?
集合中的元素是互异的
问题探究
不正确.集合中只有4个不同元素1,3,0,5
.
3.高一(5)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
集合中的元素是没有顺序的
通过以上的学习你能给出集合中元素的特性吗?
确定性、互异性、无序性
问题探究
集合没有变化
只要构成两个集合的元素是一样,我们就称
这两个集合是相等的。
集合中元素的三个特性
集合中元素是确定的,即对任何一个对象,
它是或不是某个集合的元素是确定的,且
二者必居其一.
确定性是判断一组对象能否构成集合的标准.
确定性
互异性
无序性
集合中的元素没有相同的,解题时这一点
易被忽视.
集合中的元素没有前后顺序.
归纳升华
启示:任何集合的元素都不能违背确定性、互异性、无序性.我们还可以用这些性质继续去探求集合与元素的关系.
1.判断以下元素的全体是否组成集合,并说明理由:
(1)
大于3小于11的偶数;
(2)
我国的小河流.
【提示】(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
学以致用
3.已知下面的两个实例:
(1)用A表示高一(8)班全体学生组成的集合.
(2)用a表示高一(8)班的一位同学,b表示高一(7)
班的一位同学.
a是集合A中的元素,
b不是集合A中的元素.
探究3:
元素和集合的关系
问题探究
思考:那么a,b与集合A分别有什么关系?
元素a与集合A的关系
如果a是集合A的元素,就说
a
属于集合A,
记作:a∈A
;
如果a不是集合A中的元素,就说
a
不属于集合A,
记作:a
?
A.
归纳总结
常用的数集
自然数集
正整数集
整数集
有理数集
实数集
记法
——
————
——
——
——
N
Z
Q
R
N
或N+
N
N
或N+
Z
N
或N+
学习集合与元素的概念后,为了方便书写,数学中规定了一些常用数集及其记法:
归纳总结
例2
用符号“∈”或“?”填空.
(1)2
N.
(2)
____________Q.
(3)0
{0}.
(4)b
{a,b,c}.
【总结提升】求解此类问题必须要做到以下两点:
①熟记常见的数集的符号;
②正确理解元素与集合之间的“属于”关系.
问题思考
“地球上的四大洋”组成集合可以表示为:
{太平洋,大西洋,印度洋,北冰洋}.
“方程x2-3x+2=0的所有实数根”,可以表示:
{1,2}
集合的表示方法
像这样把集合的元素一一列举出来,并用花
括号“{
}”括起来表示集合的方法叫做列举法.
集合的元素用“,”号分开.
用列举法表示下列集合:
(1)小于10的所有的自然数组成的集合;
(2)方程
x
2=x
的解;
(1)大括号不能缺失.
(2)有些集合元素个数较多,元素又呈现出一定的规律,在不至于发生误解的情况下,亦可如下表示:从1到100的所有整数组成的集合:{1,2,3,…,100}
自然数集N:{1,2,3,4,…,n,…}
(3)区分a与{a}:{a}表示一个集合,该集合只有一个元素.a表示这个集合的一个元素.
(4)用列举法表示集合时不必考虑元素的前后次序.相同的元素不能出现两次.
注意
用列举法表示出集合:{(1,2),(2,3)}
表示是什么样集合?
所有的集合都可以用列表法来表示吗?比如:不等式x-7<3的解集能用列举法吗?为什么?那么怎样来表示这个集合呢?
这个集合中的元素是列举不完的,可以用集合所含元素的共同特征表示集合.
集合的表示方法三:
不等式x-7<3的解是x<10,有无数个集,我们可以用解集中元素的共同特征,把解集表示:
整数集Z可以分为奇数集和偶数集,利用奇数的特征表示所有奇数:
用利用偶数的特征,表示所有偶数:
实数集R中,有限小数和无限循环小数都可以表示成分数形式,
则有理数集可以表示
描述法:用确定的条件表示某些对象是否属于这个集合的方法.
具体方法:
在花括号内先写上表示这个集合元素的一般符号及取值范围,在画一条竖线,在竖线后写出这个集合中的元素所具有的共同特征.
{x|
P(x)}或{x∈A|
P(x)}
含义:在集合A中满足条件P(x)的x的集合.
集合的表示方法三:
1.使用描述法表示下列集合:
(1)
不等式2x-1>3的解集A;
(2)由大于10且小于20的所有整数组成的集合B
(3)方程
x2
-2=0
的所有实数根组成的集合;
(4)方程组
的解集.
做一做
{(3.5,-1.5)}
2.方程组
的解集用列举法表示为
__________________________
;
用描述法表示为______________________.
用列举法表示为
{(0,6),(1,5),(2,4),(3,3),(6,0),(5,1),(4,2)}
?
有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法.
有些集合的元素不能无遗漏地一一列举出来,或者不便于、不需要一一列举出来,常用描述法.
何时用列举法,何时
用描述法更容易一
些呢?
集合的表示方法四:
韦恩图:用一条封闭的曲线的内部来表示一个集合.
有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法.
集合A
集合B
1.已知集合A含有三个元素a+2,(a+1)2,a2+3a+3,若1∈A,求实数a的值.
【解析】因为1∈A,所以
①若a+2=1,解得a=-1,此时集合含有1,0,1三个元素,元素重复,所以不成立,即a≠-1.
②若(a+1)2=1,解得a=0或a=-2,当a=0时,集合A含有2,1,3三个元素,满足条件,即a=0成立.
典型题一:元素的互异性典型题一:元素的互异性
当a=-2时,集合A含有0,1,1三个元素,
元素重复,所以不成立,即a≠-2.
③
若a2+3a+3=1,解得a=-1或a=-2,由①②知都
不成立.
所以满足条件的实数a的取值为0,即a=0.
典型题一:元素的互异性典型题一:元素的互异性
(2)若{1,
2,a2-1}={1,a2-a,0},则
a=_________.
(3)若{1,2}={a-2,2h},则求
a,
h?
1.集合
与集合
是同一集合吗?
答:不是.集合
是点集,集合
是数集.
典型题二:描述法典型题二:描述法
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
