人教版 五年级数学上册1.2小数乘法2同步学案(含答案)
文档属性
| 名称 | 人教版 五年级数学上册1.2小数乘法2同步学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2讲 小数乘法2
一、积的近似数
【知识梳理】
1.求近似数的方法一般有三种:
(1)四舍五入法;
(2)进一法;
(3)去尾法。
【典例精讲】
例1.一个长方形风景框,长5.8分米,宽2.8分米,要给16个这样的风景框的四周镶上铝制边框,至少需要多长的铝条?(接头处忽略不计,得数保留整数)
例2.按要求保留积的小数位数。
例3.某日,1美元兑换人民币约6.713元,1港元兑换人民币约0.855元。
(1)妈妈在香港给王欣买了一个芭比娃娃,定价23.8港元,折合人民币约是多少元?(得数保留两位小数)
(2)在美国的姨妈给王欣买了一个文具盒,定价4.8美元,折合人民币约是多少元?(得数保留两位小数)
例4.判一判。
(1)8.23精确到十位约是8.3。( )
(2)一个三位小数,保留两位小数约是9.82,这个三位小数最小是9.815。( )
(3)21.5×0.32的积保留一位小数是6.8。( )
(4)近似数6.50和6.500大小相等,但精确度不同。( )
【巩固练习】
1.列竖式计算。
(1)得数保留一位小数。
4.23×3.4 2.54×1.3
(2)得数保留两位小数。
1.24×3.82 7.36×2.58
2.填一填。
(1)48.9952保留整数约是( ),保留一位小数约是( ),精确到百分位约是( ),保留三位小数约是( )
(2)有三个近似数0.6,0.60,0.600,这三个数大小( ),精确度( )。
(3)近似数为8.0的最大两位小数为( ),最小两位小数为( )。
(4)4.16×0.09的积是( )位小数,保留三位小数约是( )。
(5)日常生活中,购物付款时要保留到“分”,也就是说以“元”为单位要保留( )位小数。
3.两个一位小数的积“四舍五入”后约是13.7,已知这两个一位小数十分位上的数字都是7,则它们的积在“四舍五入”前是多少?
4.两个长方形的房间,大房的长5.2,宽4.6,小房的长3.4,宽2.7,不用精确计算,估计大房的面积超过 ,小房的面积不超过 .
5.刘大叔从水果批发市场批发了一些柚子,总价“四含五入”后约是89.6元。柚子的单价和质量都是一位小数,且十分位上的数字都是6,柚子的总价在“四含五入”前是多少元?
二、整数乘法运算律推广到小数
【知识梳理】
1.整数乘法的交换律、结合律和分配律对于小数乘法同样适用。
乘法交换律:;
乘法结合律:;
乘法分配律:;变式:。
【说明】运用乘法分配律进行简算时,公共的因数要和两个加数分别相乘。
2.用简便方法计算小数乘法时,从不同的角度思考,有时可以得出不同的简算方法。
3.小数四则运算顺序和整数四则混合运算的顺序相同。
【例题精讲】
例1.大象的奔跑速度最快可达每小时38.6千米,长颈鹿奔跑的最快速度是它的1.33倍.长颈鹿的最快速度是每小时多少千米?(得数保留两位小数)
例2.算一算,比一比。
0.67×4.68 4.68×0.67
25×0.73×0.4 (25×0.4)×0.73
5.6×10.1 5.6×10+5.6×0.1
7.5×4.3+5.7×7.5 (4.3+5.7)×7.5
例3.在里□填上数,在〇里填上运算符号,在横线上填上所运用的运算定律。
(1)5.6×3.8=□〇5.6 _____________________;
(2)12.5×0.7×0.8=(□〇□)×□ ;
(3)0.36×4.5+5.5×0.36=(□〇□)〇□ 。
例4.用简便方法计算。
(1)2.9×9.8+0.29+0.029×10
(2)9.5×0.35+0.95×4.2+0.095×23
【巩固练习】
1.5.05与6.3的积有__________ 位小数,得数保留两位小数约是__________ ,5.03与6.5的和有__________ 位小数,得数保留一位小数约是__________ .
2.菜场优惠销售南瓜,每千克的价格是2.58元,妈妈买了l.2千克,需要付多少元?(得数保留一位小数)
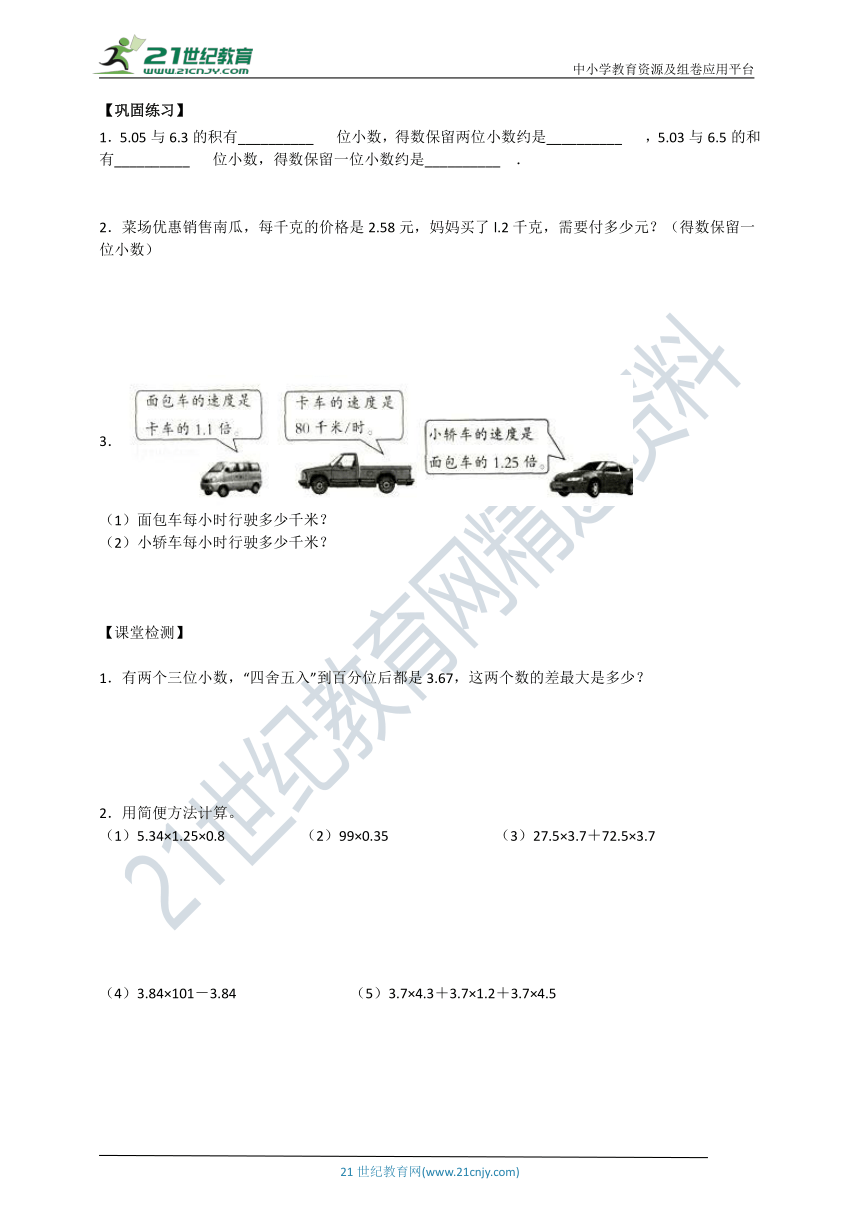
3.
(1)面包车每小时行驶多少千米?
(2)小轿车每小时行驶多少千米?
【课堂检测】
1.有两个三位小数,“四舍五入”到百分位后都是3.67,这两个数的差最大是多少?
2.用简便方法计算。
(1)5.34×1.25×0.8 (2)99×0.35 (3)27.5×3.7+72.5×3.7
(4)3.84×101-3.84 (5)3.7×4.3+3.7×1.2+3.7×4.5
两个一位小数的乘积“四舍五人”后是l3.7,这两个一位小数的十分位都是7,这两个小数的乘积在四舍五入前是多少?
4.两个因数的积是8.86,如果把一个因数扩大到原来的10倍,另一个因数缩小到原来的,那么积是( ).
5.赵叔叔拿26欧元去兑换人民币,如果1欧元可以兑换6.79元,那么赵叔叔一共可以兑换人民币多少钱?
6.求下面积的近似值.
0.93×5.32(结果精确到十分位)
6.05×1.24(得数保留两位小数)
参考答案
一、积的近似数
【知识梳理】
1.求近似数的方法一般有三种:
(1)四舍五入法;
(2)进一法;
(3)去尾法。
【典例精讲】
例1.一个长方形风景框,长5.8分米,宽2.8分米,要给16个这样的风景框的四周镶上铝制边框,至少需要多长的铝条?(接头处忽略不计,得数保留整数)
【解答】8.5.8+2.8=8.6(分米),8.6×2=17.2(分米),17.2×16≈276(分米)
【答案】276分米
例2.按要求保留积的小数位数。
【答案】16.9,16.92,16.919;2.5,2.50,2.498;53.9,53.87,53.869;0.1,0.11,0.113。
例3.某日,1美元兑换人民币约6.713元,1港元兑换人民币约0.855元。
(1)妈妈在香港给王欣买了一个芭比娃娃,定价23.8港元,折合人民币约是多少元?(得数保留两位小数)
(2)在美国的姨妈给王欣买了一个文具盒,定价4.8美元,折合人民币约是多少元?(得数保留两位小数)
【解答】(1)23.8×0.855≈20.35(元);(2)4.8×6.713≈32.22(元)
【答案】(1)20.35元;(2)32.22元。
例4.判一判。
(1)8.23精确到十位约是8.3。( )
(2)一个三位小数,保留两位小数约是9.82,这个三位小数最小是9.815。( )
(3)21.5×0.32的积保留一位小数是6.8。( )
(4)近似数6.50和6.500大小相等,但精确度不同。( )
【答案】(1)×;(2)√;(3)×;(4)√。
【巩固练习】
1.列竖式计算。
(1)得数保留一位小数。
4.23×3.4 2.54×1.3
(2)得数保留两位小数。
1.24×3.82 7.36×2.58
【答案】(1)14.4,3.3;(2)4.74,18.99。
2.填一填。
(1)48.9952保留整数约是( ),保留一位小数约是( ),精确到百分位约是( ),保留三位小数约是( )
(2)有三个近似数0.6,0.60,0.600,这三个数大小( ),精确度( )。
(3)近似数为8.0的最大两位小数为( ),最小两位小数为( )。
(4)4.16×0.09的积是( )位小数,保留三位小数约是( )。
(5)日常生活中,购物付款时要保留到“分”,也就是说以“元”为单位要保留( )位小数。
【答案】(1)49,49.0,49.00,48.995;(2)相等,不同;(3)8.04,7.95;(4)四,0.374;(5)两。
3.两个一位小数的积“四舍五入”后约是13.7,已知这两个一位小数十分位上的数字都是7,则它们的积在“四舍五入”前是多少?
【答案】解:13.69.
4.两个长方形的房间,大房的长5.2,宽4.6,小房的长3.4,宽2.7,不用精确计算,估计大房的面积超过 ,小房的面积不超过 .
【答案】20,12.
5.刘大叔从水果批发市场批发了一些柚子,总价“四含五入”后约是89.6元。柚子的单价和质量都是一位小数,且十分位上的数字都是6,柚子的总价在“四含五入”前是多少元?
【解答】单价和质量都是一位小数,且十分位上均为6,那么总价应为两位小数,百分位上为,“四含五入”约为89.6,则原数为89.56。
【答案】89.56元
二、整数乘法运算律推广到小数
【知识梳理】
1.整数乘法的交换律、结合律和分配律对于小数乘法同样适用。
乘法交换律:;
乘法结合律:;
乘法分配律:;变式:。
【说明】运用乘法分配律进行简算时,公共的因数要和两个加数分别相乘。
2.用简便方法计算小数乘法时,从不同的角度思考,有时可以得出不同的简算方法。
3.小数四则运算顺序和整数四则混合运算的顺序相同。
【例题精讲】
例1.大象的奔跑速度最快可达每小时38.6千米,长颈鹿奔跑的最快速度是它的1.33倍.长颈鹿的最快速度是每小时多少千米?(得数保留两位小数)
【解答】解:
38.6×1.33≈51.34(千米).
答:长颈鹿的最快速度是每小时51.34千米.
【答案】解:
38.6×1.33≈51.34(千米).
答:长颈鹿的最快速度是每小时51.34千米.
例2.算一算,比一比。
0.67×4.68 4.68×0.67
25×0.73×0.4 (25×0.4)×0.73
5.6×10.1 5.6×10+5.6×0.1
7.5×4.3+5.7×7.5 (4.3+5.7)×7.5
【答案】3.1356,3.1356;7.3,7.3;56.56,56.56;75,75。
例3.在里□填上数,在〇里填上运算符号,在横线上填上所运用的运算定律。
(1)5.6×3.8=□〇5.6 _____________________;
(2)12.5×0.7×0.8=(□〇□)×□ ;
(3)0.36×4.5+5.5×0.36=(□〇□)〇□ 。
【答案】(1)3.8,×,乘法交换律;(2)12.5,×,0.8, 0.7,乘法交换律;(3)4.5,+,5.5,×,0.36,乘法分配律。
例4.用简便方法计算。
(1)2.9×9.8+0.29+0.029×10
(2)9.5×0.35+0.95×4.2+0.095×23
【解答】(1)原式=2.9×9.8+2.9×0.1+2.9×0.1
=2.9×(9.8+0.1+0.1)
=2.9×10
=29
(2)原式=0.095×35+0.095×42+0.095×23
=(35+42+23)×0.095
=100×0.095
=9.5
【答案】(1)29;(2)9.5。
【巩固练习】
1.5.05与6.3的积有__________ 位小数,得数保留两位小数约是__________ ,5.03与6.5的和有__________ 位小数,得数保留一位小数约是__________ .
【解答】解:①5.05×6.3=31.815;
所以是3位小数.
31.815≈31.82;
②5.03+6.5=11.53
所以是两位小数,
11.53≈11.5
故答案为:3,31.82,2,11.5.
【答案】3|31.82|2|11.5
2.菜场优惠销售南瓜,每千克的价格是2.58元,妈妈买了l.2千克,需要付多少元?(得数保留一位小数)
【解答】解:2.58×1.2≈3.1(元).
答:需要付3.1元.
【答案】3.1
3.
(1)面包车每小时行驶多少千米?
(2)小轿车每小时行驶多少千米?
【解答】解:80×1.1=88(千米);
答:面包车每小时行驶88千米.
88×1.25=110(千米);
答:小轿车每小时行驶110千米.
【答案】解:80×1.1=88(千米);
答:面包车每小时行驶88千米.
88×1.25=110(千米);
答:小轿车每小时行驶110千米.
【课堂检测】
1.有两个三位小数,“四舍五入”到百分位后都是3.67,这两个数的差最大是多少?
【解答】3.674-3.665=0.009
【答案】0.009
2.用简便方法计算。
(1)5.34×1.25×0.8
(2)99×0.35
(3)27.5×3.7+72.5×3.7
(4)3.84×101-3.84
(5)3.7×4.3+3.7×1.2+3.7×4.5
【答案】(1)5.34;(2)34.65;(3)370;(4)384;(5)37。
两个一位小数的乘积“四舍五人”后是l3.7,这两个一位小数的十分位都是7,这两个小数的乘积在四舍五入前是多少?
【解答】解:
这两个一位小数的十分位都是7;7×7=49,那么乘积之后百分位是9;
四舍五入后要向前进一位后是7,那么乘积的十分位原来是6,即这两个小数的乘积是13.69.
答:这两个小数的乘积在四舍五入前是13.69.
【答案】解:
这两个一位小数的十分位都是7;7×7=49,那么乘积之后百分位是9;
四舍五入后要向前进一位后是7,那么乘积的十分位原来是6,即这两个小数的乘积是13.69.
答:这两个小数的乘积在四舍五入前是13.69.
4.两个因数的积是8.86,如果把一个因数扩大到原来的10倍,另一个因数缩小到原来的,那么积是( ).
【答案】8.86
5.赵叔叔拿26欧元去兑换人民币,如果1欧元可以兑换6.79元,那么赵叔叔一共可以兑换人民币多少钱?
【答案】解:6.79×26=176.54(元).
6.求下面积的近似值.
0.93×5.32(结果精确到十分位)
6.05×1.24(得数保留两位小数)
【解答】解:
0.93×5.32≈4.9
6.05×1.24≈7.50
【答案】解:
0.93×5.32≈4.9
6.05×1.24≈7.50
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2讲 小数乘法2
一、积的近似数
【知识梳理】
1.求近似数的方法一般有三种:
(1)四舍五入法;
(2)进一法;
(3)去尾法。
【典例精讲】
例1.一个长方形风景框,长5.8分米,宽2.8分米,要给16个这样的风景框的四周镶上铝制边框,至少需要多长的铝条?(接头处忽略不计,得数保留整数)
例2.按要求保留积的小数位数。
例3.某日,1美元兑换人民币约6.713元,1港元兑换人民币约0.855元。
(1)妈妈在香港给王欣买了一个芭比娃娃,定价23.8港元,折合人民币约是多少元?(得数保留两位小数)
(2)在美国的姨妈给王欣买了一个文具盒,定价4.8美元,折合人民币约是多少元?(得数保留两位小数)
例4.判一判。
(1)8.23精确到十位约是8.3。( )
(2)一个三位小数,保留两位小数约是9.82,这个三位小数最小是9.815。( )
(3)21.5×0.32的积保留一位小数是6.8。( )
(4)近似数6.50和6.500大小相等,但精确度不同。( )
【巩固练习】
1.列竖式计算。
(1)得数保留一位小数。
4.23×3.4 2.54×1.3
(2)得数保留两位小数。
1.24×3.82 7.36×2.58
2.填一填。
(1)48.9952保留整数约是( ),保留一位小数约是( ),精确到百分位约是( ),保留三位小数约是( )
(2)有三个近似数0.6,0.60,0.600,这三个数大小( ),精确度( )。
(3)近似数为8.0的最大两位小数为( ),最小两位小数为( )。
(4)4.16×0.09的积是( )位小数,保留三位小数约是( )。
(5)日常生活中,购物付款时要保留到“分”,也就是说以“元”为单位要保留( )位小数。
3.两个一位小数的积“四舍五入”后约是13.7,已知这两个一位小数十分位上的数字都是7,则它们的积在“四舍五入”前是多少?
4.两个长方形的房间,大房的长5.2,宽4.6,小房的长3.4,宽2.7,不用精确计算,估计大房的面积超过 ,小房的面积不超过 .
5.刘大叔从水果批发市场批发了一些柚子,总价“四含五入”后约是89.6元。柚子的单价和质量都是一位小数,且十分位上的数字都是6,柚子的总价在“四含五入”前是多少元?
二、整数乘法运算律推广到小数
【知识梳理】
1.整数乘法的交换律、结合律和分配律对于小数乘法同样适用。
乘法交换律:;
乘法结合律:;
乘法分配律:;变式:。
【说明】运用乘法分配律进行简算时,公共的因数要和两个加数分别相乘。
2.用简便方法计算小数乘法时,从不同的角度思考,有时可以得出不同的简算方法。
3.小数四则运算顺序和整数四则混合运算的顺序相同。
【例题精讲】
例1.大象的奔跑速度最快可达每小时38.6千米,长颈鹿奔跑的最快速度是它的1.33倍.长颈鹿的最快速度是每小时多少千米?(得数保留两位小数)
例2.算一算,比一比。
0.67×4.68 4.68×0.67
25×0.73×0.4 (25×0.4)×0.73
5.6×10.1 5.6×10+5.6×0.1
7.5×4.3+5.7×7.5 (4.3+5.7)×7.5
例3.在里□填上数,在〇里填上运算符号,在横线上填上所运用的运算定律。
(1)5.6×3.8=□〇5.6 _____________________;
(2)12.5×0.7×0.8=(□〇□)×□ ;
(3)0.36×4.5+5.5×0.36=(□〇□)〇□ 。
例4.用简便方法计算。
(1)2.9×9.8+0.29+0.029×10
(2)9.5×0.35+0.95×4.2+0.095×23
【巩固练习】
1.5.05与6.3的积有__________ 位小数,得数保留两位小数约是__________ ,5.03与6.5的和有__________ 位小数,得数保留一位小数约是__________ .
2.菜场优惠销售南瓜,每千克的价格是2.58元,妈妈买了l.2千克,需要付多少元?(得数保留一位小数)
3.
(1)面包车每小时行驶多少千米?
(2)小轿车每小时行驶多少千米?
【课堂检测】
1.有两个三位小数,“四舍五入”到百分位后都是3.67,这两个数的差最大是多少?
2.用简便方法计算。
(1)5.34×1.25×0.8 (2)99×0.35 (3)27.5×3.7+72.5×3.7
(4)3.84×101-3.84 (5)3.7×4.3+3.7×1.2+3.7×4.5
两个一位小数的乘积“四舍五人”后是l3.7,这两个一位小数的十分位都是7,这两个小数的乘积在四舍五入前是多少?
4.两个因数的积是8.86,如果把一个因数扩大到原来的10倍,另一个因数缩小到原来的,那么积是( ).
5.赵叔叔拿26欧元去兑换人民币,如果1欧元可以兑换6.79元,那么赵叔叔一共可以兑换人民币多少钱?
6.求下面积的近似值.
0.93×5.32(结果精确到十分位)
6.05×1.24(得数保留两位小数)
参考答案
一、积的近似数
【知识梳理】
1.求近似数的方法一般有三种:
(1)四舍五入法;
(2)进一法;
(3)去尾法。
【典例精讲】
例1.一个长方形风景框,长5.8分米,宽2.8分米,要给16个这样的风景框的四周镶上铝制边框,至少需要多长的铝条?(接头处忽略不计,得数保留整数)
【解答】8.5.8+2.8=8.6(分米),8.6×2=17.2(分米),17.2×16≈276(分米)
【答案】276分米
例2.按要求保留积的小数位数。
【答案】16.9,16.92,16.919;2.5,2.50,2.498;53.9,53.87,53.869;0.1,0.11,0.113。
例3.某日,1美元兑换人民币约6.713元,1港元兑换人民币约0.855元。
(1)妈妈在香港给王欣买了一个芭比娃娃,定价23.8港元,折合人民币约是多少元?(得数保留两位小数)
(2)在美国的姨妈给王欣买了一个文具盒,定价4.8美元,折合人民币约是多少元?(得数保留两位小数)
【解答】(1)23.8×0.855≈20.35(元);(2)4.8×6.713≈32.22(元)
【答案】(1)20.35元;(2)32.22元。
例4.判一判。
(1)8.23精确到十位约是8.3。( )
(2)一个三位小数,保留两位小数约是9.82,这个三位小数最小是9.815。( )
(3)21.5×0.32的积保留一位小数是6.8。( )
(4)近似数6.50和6.500大小相等,但精确度不同。( )
【答案】(1)×;(2)√;(3)×;(4)√。
【巩固练习】
1.列竖式计算。
(1)得数保留一位小数。
4.23×3.4 2.54×1.3
(2)得数保留两位小数。
1.24×3.82 7.36×2.58
【答案】(1)14.4,3.3;(2)4.74,18.99。
2.填一填。
(1)48.9952保留整数约是( ),保留一位小数约是( ),精确到百分位约是( ),保留三位小数约是( )
(2)有三个近似数0.6,0.60,0.600,这三个数大小( ),精确度( )。
(3)近似数为8.0的最大两位小数为( ),最小两位小数为( )。
(4)4.16×0.09的积是( )位小数,保留三位小数约是( )。
(5)日常生活中,购物付款时要保留到“分”,也就是说以“元”为单位要保留( )位小数。
【答案】(1)49,49.0,49.00,48.995;(2)相等,不同;(3)8.04,7.95;(4)四,0.374;(5)两。
3.两个一位小数的积“四舍五入”后约是13.7,已知这两个一位小数十分位上的数字都是7,则它们的积在“四舍五入”前是多少?
【答案】解:13.69.
4.两个长方形的房间,大房的长5.2,宽4.6,小房的长3.4,宽2.7,不用精确计算,估计大房的面积超过 ,小房的面积不超过 .
【答案】20,12.
5.刘大叔从水果批发市场批发了一些柚子,总价“四含五入”后约是89.6元。柚子的单价和质量都是一位小数,且十分位上的数字都是6,柚子的总价在“四含五入”前是多少元?
【解答】单价和质量都是一位小数,且十分位上均为6,那么总价应为两位小数,百分位上为,“四含五入”约为89.6,则原数为89.56。
【答案】89.56元
二、整数乘法运算律推广到小数
【知识梳理】
1.整数乘法的交换律、结合律和分配律对于小数乘法同样适用。
乘法交换律:;
乘法结合律:;
乘法分配律:;变式:。
【说明】运用乘法分配律进行简算时,公共的因数要和两个加数分别相乘。
2.用简便方法计算小数乘法时,从不同的角度思考,有时可以得出不同的简算方法。
3.小数四则运算顺序和整数四则混合运算的顺序相同。
【例题精讲】
例1.大象的奔跑速度最快可达每小时38.6千米,长颈鹿奔跑的最快速度是它的1.33倍.长颈鹿的最快速度是每小时多少千米?(得数保留两位小数)
【解答】解:
38.6×1.33≈51.34(千米).
答:长颈鹿的最快速度是每小时51.34千米.
【答案】解:
38.6×1.33≈51.34(千米).
答:长颈鹿的最快速度是每小时51.34千米.
例2.算一算,比一比。
0.67×4.68 4.68×0.67
25×0.73×0.4 (25×0.4)×0.73
5.6×10.1 5.6×10+5.6×0.1
7.5×4.3+5.7×7.5 (4.3+5.7)×7.5
【答案】3.1356,3.1356;7.3,7.3;56.56,56.56;75,75。
例3.在里□填上数,在〇里填上运算符号,在横线上填上所运用的运算定律。
(1)5.6×3.8=□〇5.6 _____________________;
(2)12.5×0.7×0.8=(□〇□)×□ ;
(3)0.36×4.5+5.5×0.36=(□〇□)〇□ 。
【答案】(1)3.8,×,乘法交换律;(2)12.5,×,0.8, 0.7,乘法交换律;(3)4.5,+,5.5,×,0.36,乘法分配律。
例4.用简便方法计算。
(1)2.9×9.8+0.29+0.029×10
(2)9.5×0.35+0.95×4.2+0.095×23
【解答】(1)原式=2.9×9.8+2.9×0.1+2.9×0.1
=2.9×(9.8+0.1+0.1)
=2.9×10
=29
(2)原式=0.095×35+0.095×42+0.095×23
=(35+42+23)×0.095
=100×0.095
=9.5
【答案】(1)29;(2)9.5。
【巩固练习】
1.5.05与6.3的积有__________ 位小数,得数保留两位小数约是__________ ,5.03与6.5的和有__________ 位小数,得数保留一位小数约是__________ .
【解答】解:①5.05×6.3=31.815;
所以是3位小数.
31.815≈31.82;
②5.03+6.5=11.53
所以是两位小数,
11.53≈11.5
故答案为:3,31.82,2,11.5.
【答案】3|31.82|2|11.5
2.菜场优惠销售南瓜,每千克的价格是2.58元,妈妈买了l.2千克,需要付多少元?(得数保留一位小数)
【解答】解:2.58×1.2≈3.1(元).
答:需要付3.1元.
【答案】3.1
3.
(1)面包车每小时行驶多少千米?
(2)小轿车每小时行驶多少千米?
【解答】解:80×1.1=88(千米);
答:面包车每小时行驶88千米.
88×1.25=110(千米);
答:小轿车每小时行驶110千米.
【答案】解:80×1.1=88(千米);
答:面包车每小时行驶88千米.
88×1.25=110(千米);
答:小轿车每小时行驶110千米.
【课堂检测】
1.有两个三位小数,“四舍五入”到百分位后都是3.67,这两个数的差最大是多少?
【解答】3.674-3.665=0.009
【答案】0.009
2.用简便方法计算。
(1)5.34×1.25×0.8
(2)99×0.35
(3)27.5×3.7+72.5×3.7
(4)3.84×101-3.84
(5)3.7×4.3+3.7×1.2+3.7×4.5
【答案】(1)5.34;(2)34.65;(3)370;(4)384;(5)37。
两个一位小数的乘积“四舍五人”后是l3.7,这两个一位小数的十分位都是7,这两个小数的乘积在四舍五入前是多少?
【解答】解:
这两个一位小数的十分位都是7;7×7=49,那么乘积之后百分位是9;
四舍五入后要向前进一位后是7,那么乘积的十分位原来是6,即这两个小数的乘积是13.69.
答:这两个小数的乘积在四舍五入前是13.69.
【答案】解:
这两个一位小数的十分位都是7;7×7=49,那么乘积之后百分位是9;
四舍五入后要向前进一位后是7,那么乘积的十分位原来是6,即这两个小数的乘积是13.69.
答:这两个小数的乘积在四舍五入前是13.69.
4.两个因数的积是8.86,如果把一个因数扩大到原来的10倍,另一个因数缩小到原来的,那么积是( ).
【答案】8.86
5.赵叔叔拿26欧元去兑换人民币,如果1欧元可以兑换6.79元,那么赵叔叔一共可以兑换人民币多少钱?
【答案】解:6.79×26=176.54(元).
6.求下面积的近似值.
0.93×5.32(结果精确到十分位)
6.05×1.24(得数保留两位小数)
【解答】解:
0.93×5.32≈4.9
6.05×1.24≈7.50
【答案】解:
0.93×5.32≈4.9
6.05×1.24≈7.50
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
