人教版九年级数学上册 23.2.1中心对称课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册 23.2.1中心对称课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
23.2.1中心对称
1.了解中心对称、对称中心和对称点的概念
;
2.理解中心对称的性质
.
3.掌握运用中心对称的性质作图的方法
重点:中心对称的概念及性质
.
难点:中心对称的概念及性质
.
对称中心
对称点
全等图形
对称
中心对称
对称中心
对称中心
1.了解中心对称的概念
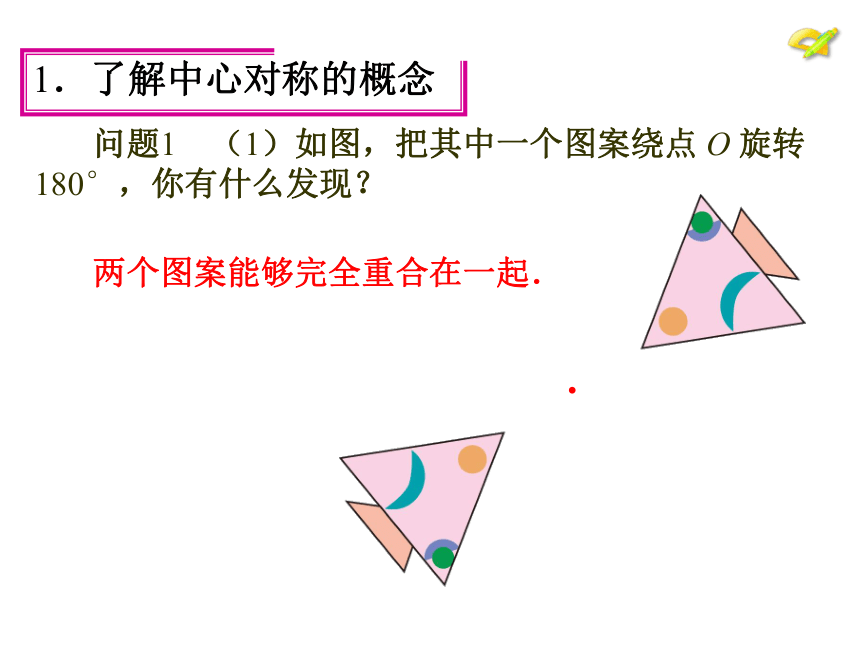
问题1 (1)如图,把其中一个图案绕点
O
旋转
180°,你有什么发现?
两个图案能够完全重合在一起.
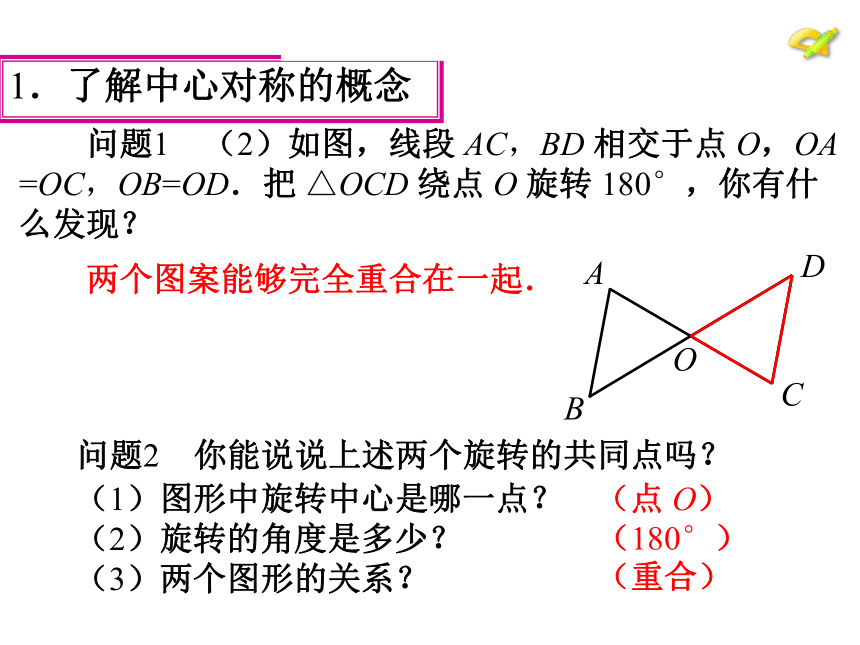
问题1 (2)如图,线段
AC,BD
相交于点
O,OA
=OC,OB=OD.把
△OCD
绕点
O
旋转
180°,你有什
么发现?
1.了解中心对称的概念
两个图案能够完全重合在一起.
A
B
D
C
O
问题2 你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
(点
O)
(180°)
(重合)
(1)学生动手操作课前准备的学具,再独立阅读教材上的相关概念:
像这样,把一个图形绕着某一个点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点叫做关于中心的对称点.
(2)细心观察成中心对称的两个图形,你有何发现?
归纳:
(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2)关于中心对称的两个图形是全等图形.
关系
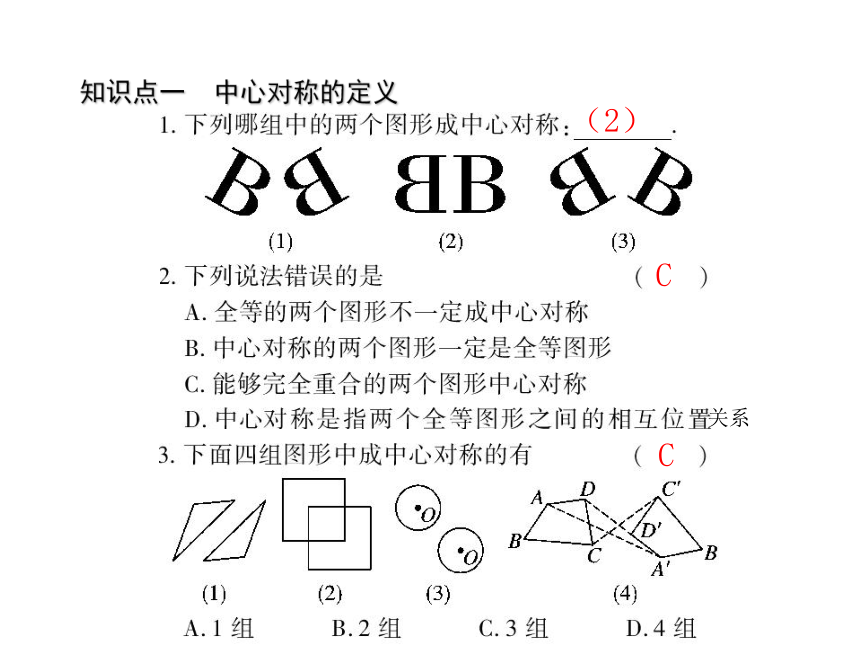
知识点一
中心对称的定义
(2)
C
C
D
知识点二
中心对称的性质
π
B
知识点二
利用旋转设计图案
B
C
例1:判断
(1)关于中心对称的两个图形是全等图形.(
)
(2)两个全等的图形一定关于中心对称.(
)
(3)能够完全重合的两个图形中心对称.(
)
(4)两个全等的图形不一定关于中心对称.
(
)
√
√
×
×
解析:
要证明OA+OB>OC,必然把OA、OB、
OC转为在一个三角形内,应用两边之和
大于第三边(两点之间线段最短)来说
明,因此要应用旋转.以A为旋转中心,旋转60°,便可把OA、OB、OC转化为一个三角形内.
例2:如图等边△ABC内有一点O,试说明:OA+OB>OC.
解:
∵如图,把△AOC以A为旋转中心顺时
针方向旋转60°后,到△AO’B的位置,
则△AOC≌△AO’B.
∴AO=AO′,OC=O′B
∴△AO′O为等边三角形.∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC
又∵∠OAO′=60°,
解析:
中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
例3:如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
(2)同样画出点B和点C的对称点E和F.
解:
(3)顺次连结DE、EF、FD.
则△DEF即为所求的三角形.
D
E
F
(4)
B
(3)
(5)
(3)
C
解:
(1)见图。
(2)对称轴有4条,至少旋转90°与自身重合.
中心对称的性质:
1.关于中心对称的两个图形,对称点所连线
段都经过对称中心,而且被对称中心所平分.
2.关于中心对称的两个图形是全等图形.
教科书第
66
页,练习
1,2
题.
23.2.1中心对称
1.了解中心对称、对称中心和对称点的概念
;
2.理解中心对称的性质
.
3.掌握运用中心对称的性质作图的方法
重点:中心对称的概念及性质
.
难点:中心对称的概念及性质
.
对称中心
对称点
全等图形
对称
中心对称
对称中心
对称中心
1.了解中心对称的概念
问题1 (1)如图,把其中一个图案绕点
O
旋转
180°,你有什么发现?
两个图案能够完全重合在一起.
问题1 (2)如图,线段
AC,BD
相交于点
O,OA
=OC,OB=OD.把
△OCD
绕点
O
旋转
180°,你有什
么发现?
1.了解中心对称的概念
两个图案能够完全重合在一起.
A
B
D
C
O
问题2 你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
(点
O)
(180°)
(重合)
(1)学生动手操作课前准备的学具,再独立阅读教材上的相关概念:
像这样,把一个图形绕着某一个点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点叫做关于中心的对称点.
(2)细心观察成中心对称的两个图形,你有何发现?
归纳:
(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2)关于中心对称的两个图形是全等图形.
关系
知识点一
中心对称的定义
(2)
C
C
D
知识点二
中心对称的性质
π
B
知识点二
利用旋转设计图案
B
C
例1:判断
(1)关于中心对称的两个图形是全等图形.(
)
(2)两个全等的图形一定关于中心对称.(
)
(3)能够完全重合的两个图形中心对称.(
)
(4)两个全等的图形不一定关于中心对称.
(
)
√
√
×
×
解析:
要证明OA+OB>OC,必然把OA、OB、
OC转为在一个三角形内,应用两边之和
大于第三边(两点之间线段最短)来说
明,因此要应用旋转.以A为旋转中心,旋转60°,便可把OA、OB、OC转化为一个三角形内.
例2:如图等边△ABC内有一点O,试说明:OA+OB>OC.
解:
∵如图,把△AOC以A为旋转中心顺时
针方向旋转60°后,到△AO’B的位置,
则△AOC≌△AO’B.
∴AO=AO′,OC=O′B
∴△AO′O为等边三角形.∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC
又∵∠OAO′=60°,
解析:
中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
例3:如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
(2)同样画出点B和点C的对称点E和F.
解:
(3)顺次连结DE、EF、FD.
则△DEF即为所求的三角形.
D
E
F
(4)
B
(3)
(5)
(3)
C
解:
(1)见图。
(2)对称轴有4条,至少旋转90°与自身重合.
中心对称的性质:
1.关于中心对称的两个图形,对称点所连线
段都经过对称中心,而且被对称中心所平分.
2.关于中心对称的两个图形是全等图形.
教科书第
66
页,练习
1,2
题.
同课章节目录
