人教版九年级上册23.3课题学习图案设计课件(15张PPT)
文档属性
| 名称 | 人教版九年级上册23.3课题学习图案设计课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
23.3课题学习图案设计
利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案。
重点:设计图案
.
难点:如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案
.
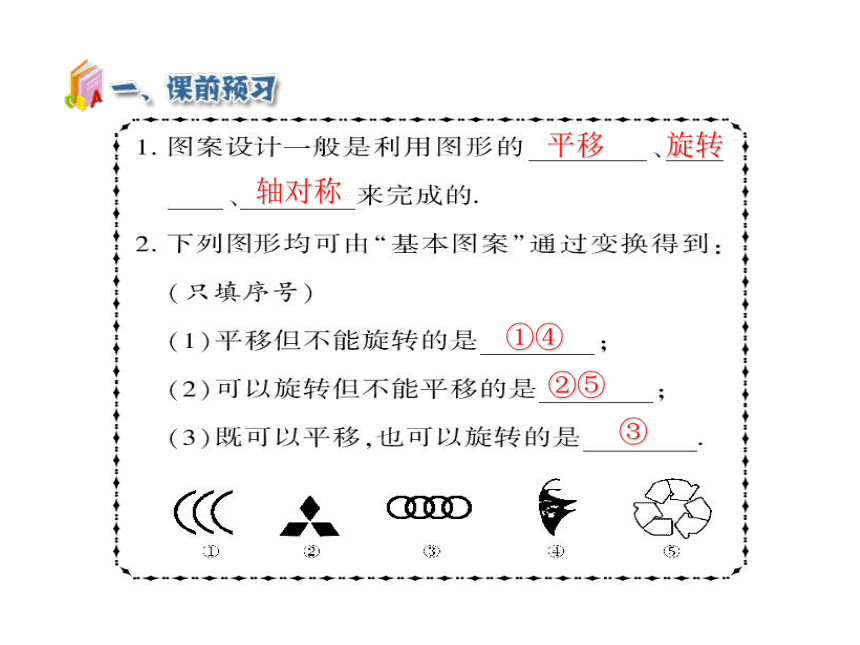
旋转
平移
①④
轴对称
②⑤
③
教师引导学生回顾以下问题:
(1)平移、旋转和轴对称变换的基本特征;
(2)归纳三种图形变换的共性。
(学生思考后回答:学生互相点评后,教师对学生的回答
进行及时的总评。)
知识点
利用图形变换设计图案
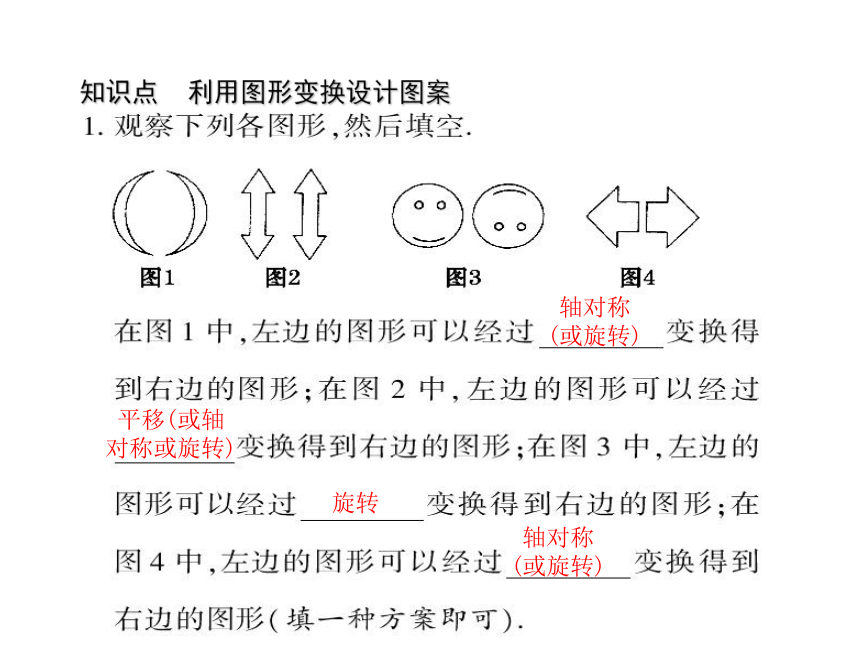
轴对称
(或旋转)
平移(或轴
对称或旋转)
旋转
轴对称
(或旋转)
A
知识点
利用图形变换设计图案
例1:图中的4个图案中,是由基本图形经过旋转得到的是_________(只写出图案序号即可)
解析:
图案①、图案②是由基本图形经过平移得到的;图案③、图案④是由基本图形经过旋转得到的.
答案:③④
例2:在图所示的4个图案中既包含图形的旋转,还有图形轴对称是(
)
解析:
分清旋转和轴对称的区别。
D
例3:在等腰直角△ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,作出点B′并求BB′的长度.
解:
连结BO并延长BO到B′,使得OB′=OB.可得点B′.
等腰直角△ABC中,∠C=90°,BC=2cm,
B’
例3:在等腰直角△ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,作出点B′并求BB′的长度.
解:
连结BO并延长BO到B′,使得OB′=OB.可得点B′.
等腰直角△ABC中,∠C=90°,BC=2cm,
B’
C
A
解:
本题答案不唯一,抓住基本图形进行巧妙的设计,如:
引导学生主要从怎样进行图案设计入手谈体会,教师概括、归纳:
①确定一个基本图案,如三角形等;
②局部平移或轴对称或旋转若干次;
③整体平移或轴对称或旋转若干次,呈现美妙图案。可见设计图案的关键是确定一个基本图案。
课后作业.
23.3课题学习图案设计
利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案。
重点:设计图案
.
难点:如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案
.
旋转
平移
①④
轴对称
②⑤
③
教师引导学生回顾以下问题:
(1)平移、旋转和轴对称变换的基本特征;
(2)归纳三种图形变换的共性。
(学生思考后回答:学生互相点评后,教师对学生的回答
进行及时的总评。)
知识点
利用图形变换设计图案
轴对称
(或旋转)
平移(或轴
对称或旋转)
旋转
轴对称
(或旋转)
A
知识点
利用图形变换设计图案
例1:图中的4个图案中,是由基本图形经过旋转得到的是_________(只写出图案序号即可)
解析:
图案①、图案②是由基本图形经过平移得到的;图案③、图案④是由基本图形经过旋转得到的.
答案:③④
例2:在图所示的4个图案中既包含图形的旋转,还有图形轴对称是(
)
解析:
分清旋转和轴对称的区别。
D
例3:在等腰直角△ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,作出点B′并求BB′的长度.
解:
连结BO并延长BO到B′,使得OB′=OB.可得点B′.
等腰直角△ABC中,∠C=90°,BC=2cm,
B’
例3:在等腰直角△ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,作出点B′并求BB′的长度.
解:
连结BO并延长BO到B′,使得OB′=OB.可得点B′.
等腰直角△ABC中,∠C=90°,BC=2cm,
B’
C
A
解:
本题答案不唯一,抓住基本图形进行巧妙的设计,如:
引导学生主要从怎样进行图案设计入手谈体会,教师概括、归纳:
①确定一个基本图案,如三角形等;
②局部平移或轴对称或旋转若干次;
③整体平移或轴对称或旋转若干次,呈现美妙图案。可见设计图案的关键是确定一个基本图案。
课后作业.
同课章节目录
