苏科版九年级数学上册 2.7 弧长及扇形的面积课件(共18张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.7 弧长及扇形的面积课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 00:00:00 | ||
图片预览



文档简介
2.7 弧长及扇形的面积
n0的圆心角所对的弧长是圆周长的多少?
10的圆心角所对的弧长是圆周长的
360
1
n0的圆心角所对的弧长是圆周长的
360
n
结 论 :
如果用字母 L 表示弧长,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
L= C圆
360
n
问题1.已知⊙O半径为R,求n°圆心角所对弧长.
弧长公式
若设⊙O半径为R, n°的圆心角所对的弧长为l,则
注意:在应用弧长公式l , 进行计算时,要注意公式中n的意义.n是不带单位的。
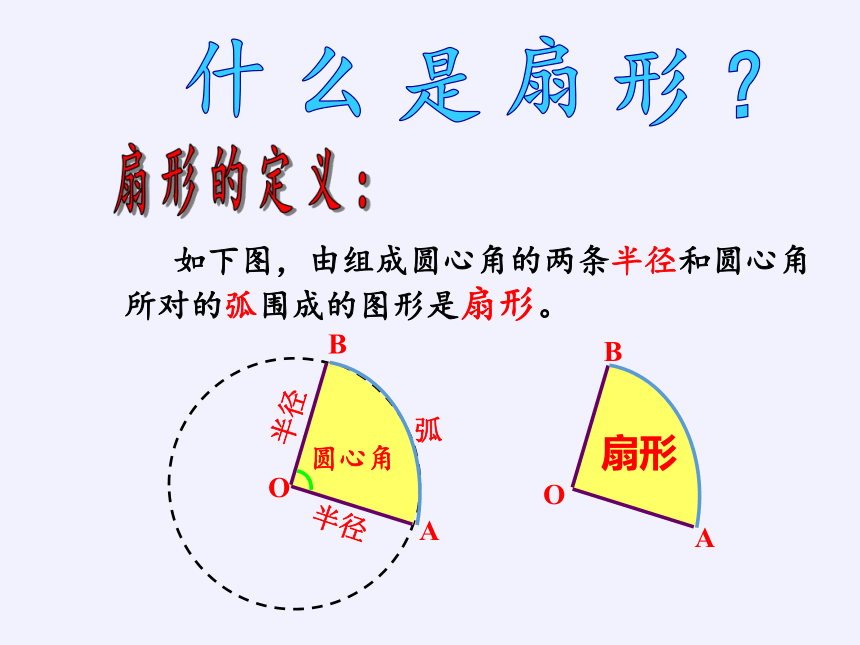
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
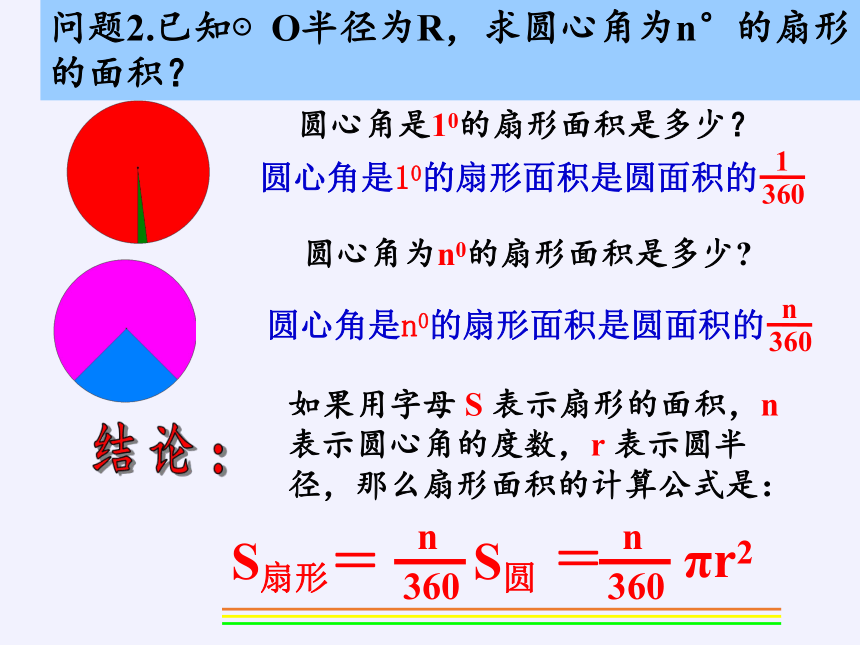
圆心角是10的扇形面积是多少?
圆心角为n0的扇形面积是多少?
圆心角是10的扇形面积是圆面积的
360
1
圆心角是n0的扇形面积是圆面积的
360
n
结 论 :
如果用字母 S 表示扇形的面积,n表示圆心角的度数,r 表示圆半径,那么扇形面积的计算公式是:
S扇形= S圆
360
n
360
n
= πr2
问题2.已知⊙O半径为R,求圆心角为n°的扇形的面积?
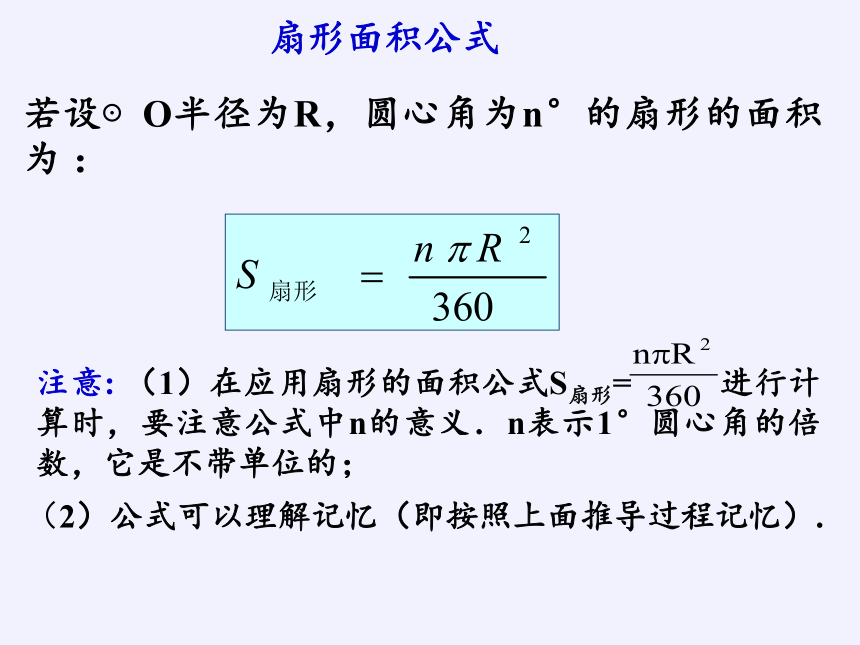
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积为 :
注意: (1)在应用扇形的面积公式S扇形= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆).
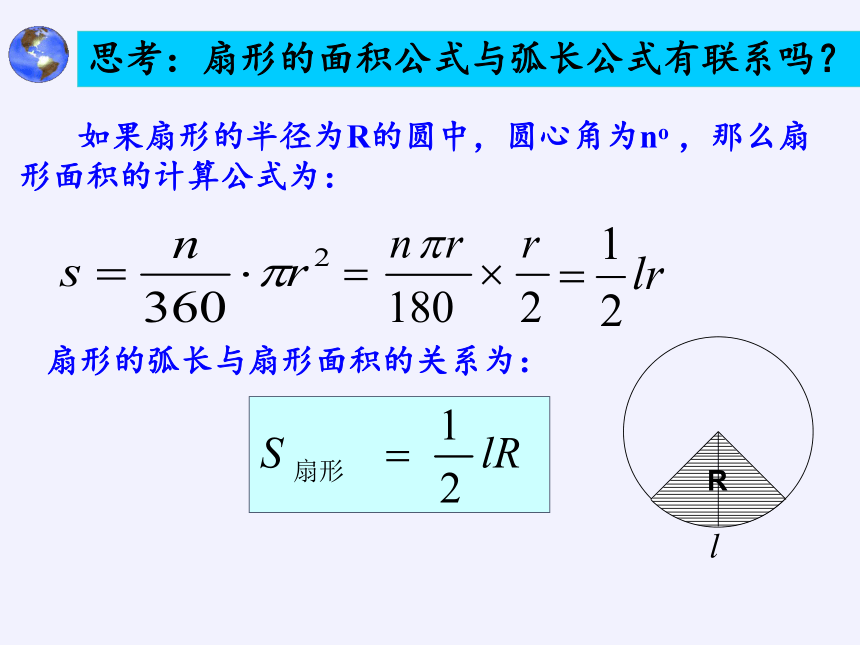
思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
R
①已知圆弧的半径为24,所对的圆心角为60°,它的弧长为____ .
②已知一弧长为12πcm,此弧所对的圆心角为240°,则此弧所在圆的半径为__.
③已知扇形的圆心角为120°,弧长为20π,扇形的面积为_ _ .
练 习
试一试
如图:在△AOC中,∠AOC=900,∠C=150,以O为
圆心,AO为半径的圆交AC与B点,若OA=6,
求弧AB的长。
A
C
B
O
例2 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.C为切点,设AB的长为d,圆环面积为S,则S与d之间有怎样的数关系?
O.
A
B
C
例3 如图,正三角形ABC的边长为a,分别以A、B、C为圆心 为半径的圆两两相切于点O1、O2、O3,求弧O1O2弧O2O3弧O3O1围成的图形的面积S(图中阴影部分).
A
B
C
O1
O2
O3
5.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于 。
例4. 如图,正方形的边长为a,以各边为直径在正方形内作半圆,求围成的图形(阴影部分)的面积.
4.(09江苏)已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为 cm(结果保留).
若正三角形的边长为6,则它的内切圆的周长为______.
△ABC的外接圆半径为2,∠BAC=60°,则弧BC的长为_____.
3、如图,⊙A、 ⊙B、
⊙C、⊙D两两不相交,
且半径都是2cm,
求图中阴影部分的面积。
巩固训练
矩形ABCD的边AB=8,AD=6,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置时(如图所示),则顶点A所经过的路线长是_________. (09黄冈)
自主探究
1、弧长、扇形面积公式;
2、不规则图形的面积的求法:用规则的图形的面积来表示;
3、数学思想转化的应用:
①转化思想;②整体思想。
小 结
谢 谢
n0的圆心角所对的弧长是圆周长的多少?
10的圆心角所对的弧长是圆周长的
360
1
n0的圆心角所对的弧长是圆周长的
360
n
结 论 :
如果用字母 L 表示弧长,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
L= C圆
360
n
问题1.已知⊙O半径为R,求n°圆心角所对弧长.
弧长公式
若设⊙O半径为R, n°的圆心角所对的弧长为l,则
注意:在应用弧长公式l , 进行计算时,要注意公式中n的意义.n是不带单位的。
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
圆心角是10的扇形面积是多少?
圆心角为n0的扇形面积是多少?
圆心角是10的扇形面积是圆面积的
360
1
圆心角是n0的扇形面积是圆面积的
360
n
结 论 :
如果用字母 S 表示扇形的面积,n表示圆心角的度数,r 表示圆半径,那么扇形面积的计算公式是:
S扇形= S圆
360
n
360
n
= πr2
问题2.已知⊙O半径为R,求圆心角为n°的扇形的面积?
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积为 :
注意: (1)在应用扇形的面积公式S扇形= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆).
思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
R
①已知圆弧的半径为24,所对的圆心角为60°,它的弧长为____ .
②已知一弧长为12πcm,此弧所对的圆心角为240°,则此弧所在圆的半径为__.
③已知扇形的圆心角为120°,弧长为20π,扇形的面积为_ _ .
练 习
试一试
如图:在△AOC中,∠AOC=900,∠C=150,以O为
圆心,AO为半径的圆交AC与B点,若OA=6,
求弧AB的长。
A
C
B
O
例2 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.C为切点,设AB的长为d,圆环面积为S,则S与d之间有怎样的数关系?
O.
A
B
C
例3 如图,正三角形ABC的边长为a,分别以A、B、C为圆心 为半径的圆两两相切于点O1、O2、O3,求弧O1O2弧O2O3弧O3O1围成的图形的面积S(图中阴影部分).
A
B
C
O1
O2
O3
5.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于 。
例4. 如图,正方形的边长为a,以各边为直径在正方形内作半圆,求围成的图形(阴影部分)的面积.
4.(09江苏)已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为 cm(结果保留).
若正三角形的边长为6,则它的内切圆的周长为______.
△ABC的外接圆半径为2,∠BAC=60°,则弧BC的长为_____.
3、如图,⊙A、 ⊙B、
⊙C、⊙D两两不相交,
且半径都是2cm,
求图中阴影部分的面积。
巩固训练
矩形ABCD的边AB=8,AD=6,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置时(如图所示),则顶点A所经过的路线长是_________. (09黄冈)
自主探究
1、弧长、扇形面积公式;
2、不规则图形的面积的求法:用规则的图形的面积来表示;
3、数学思想转化的应用:
①转化思想;②整体思想。
小 结
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
