苏科版九年级上册 数学 课件 2.4 圆周角 课件(40张PPT)
文档属性
| 名称 | 苏科版九年级上册 数学 课件 2.4 圆周角 课件(40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 918.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 00:00:00 | ||
图片预览




文档简介
2.4 圆周角
你喜欢踢足球吗?你知道足球队员之间踢球的关键是什么?
配合
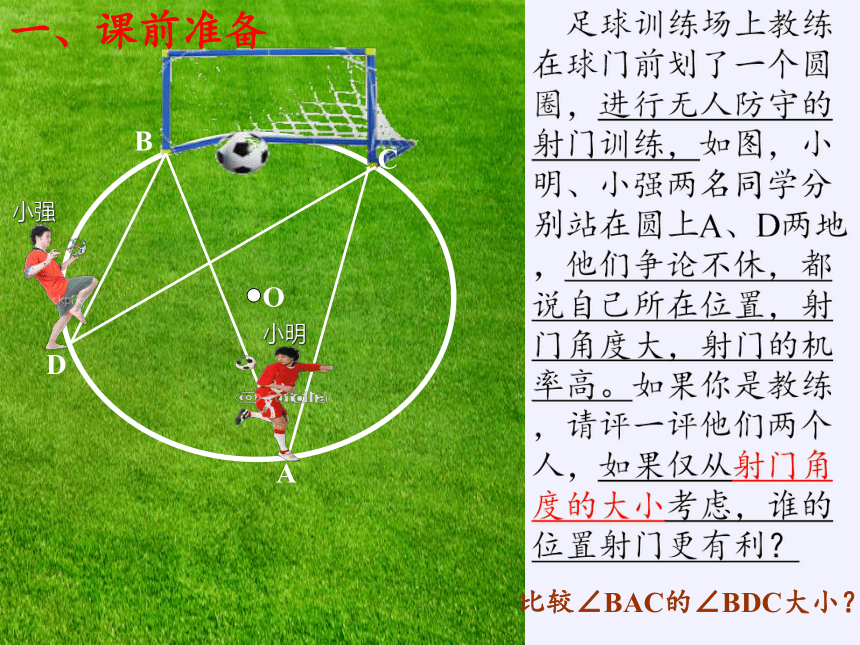
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
比较∠BAC的∠BDC大小?
小明
小强
一、课前准备
初中数学九年级上册
(苏科版)
沭阳如东实验学校初三备课组
2.4 圆周角(1)
学习目标
1.掌握圆周角的概念
2.体验并掌握圆周角定理的探究过程
3.感悟圆周角定理中数学思想方法
.
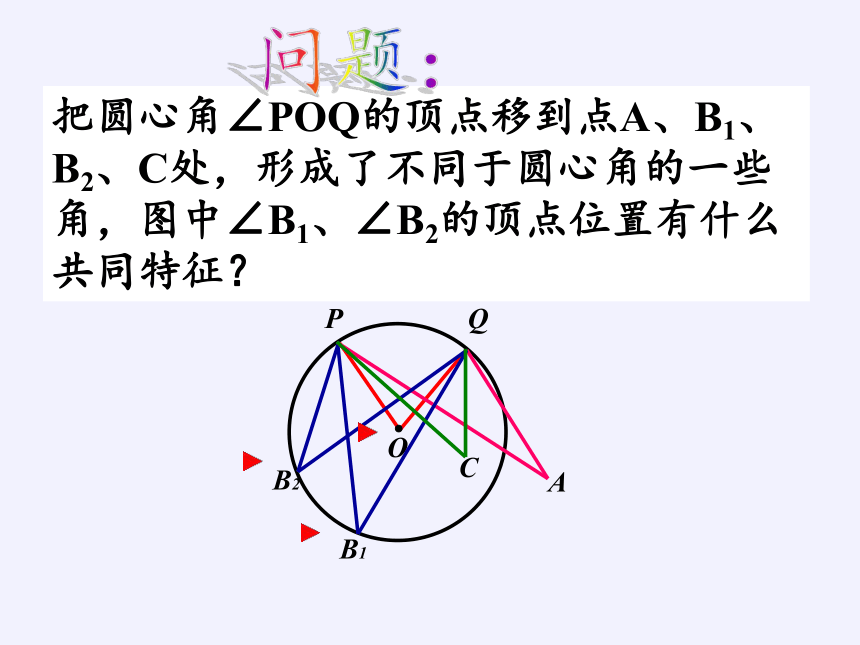
把圆心角∠POQ的顶点移到点A、B1、B2、C处,形成了不同于圆心角的一些角,图中∠B1、∠B2的顶点位置有什么共同特征?
问题:
P
Q
O
A
B1
B2
C
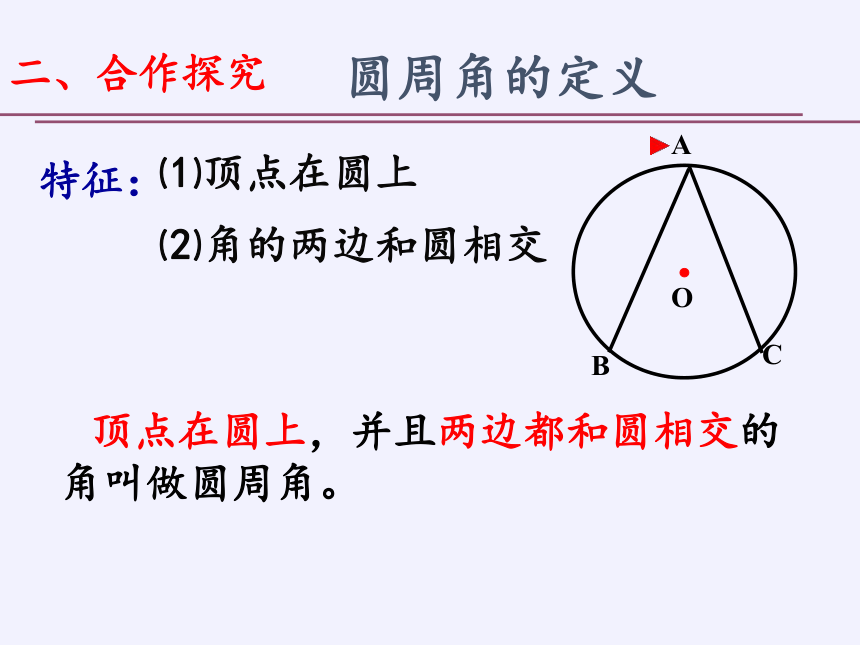
圆周角的定义
O
B
C
A
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
⑴顶点在圆上
⑵角的两边和圆相交
特征:
二、合作探究
请大家画出一个错误的圆周角。
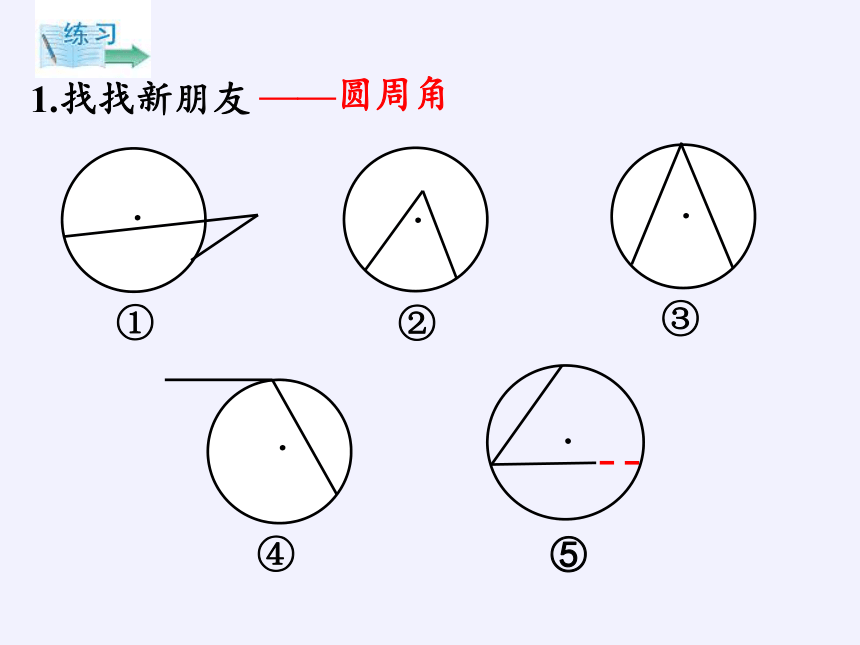
1.找找新朋友
①
.
②
.
③
.
⑤
.
④
.
——圆周角
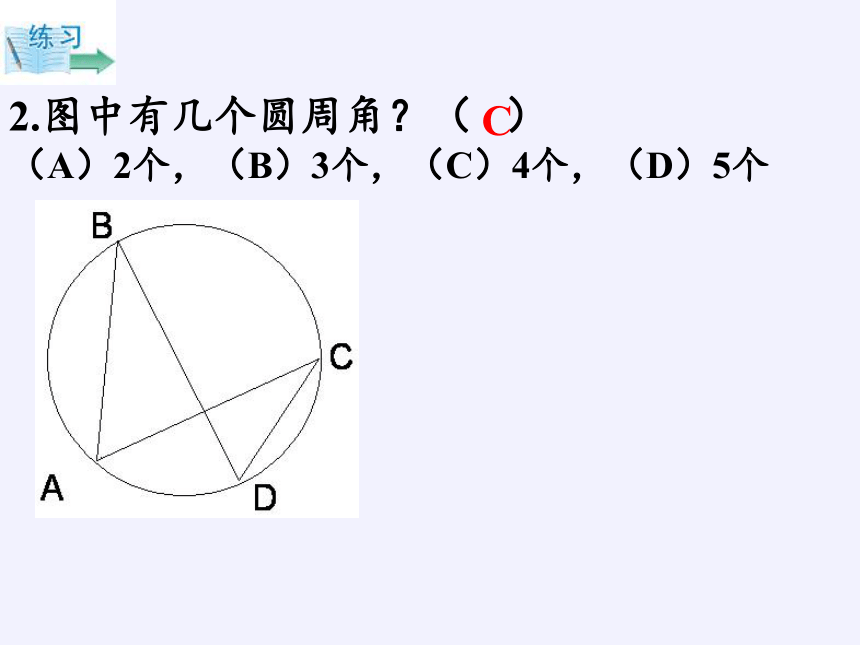
2.图中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个
C
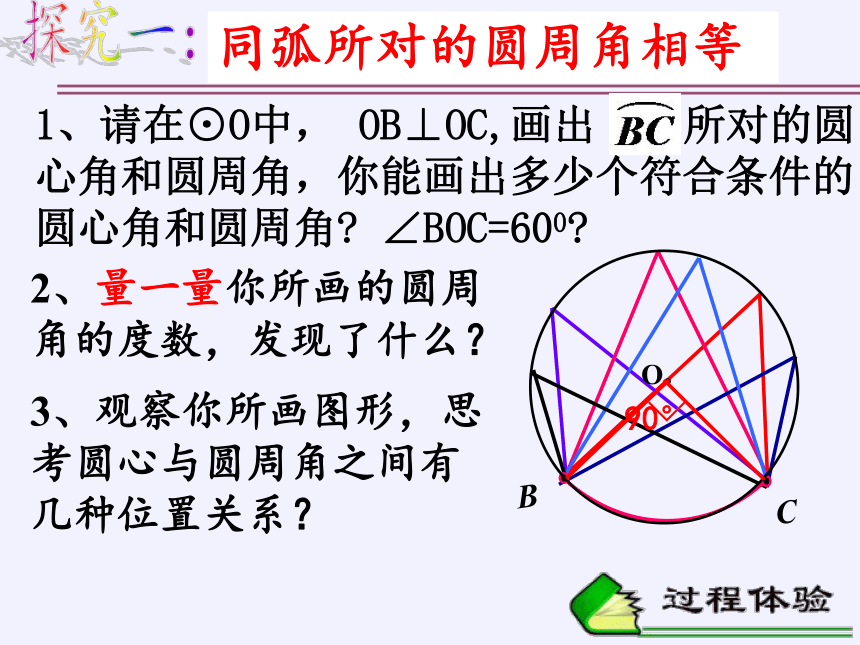
探究一:
2、量一量你所画的圆周角的度数,发现了什么?
同弧所对的圆周角相等
1、请在⊙O中, OB⊥OC,画出 所对的圆
心角和圆周角,你能画出多少个符合条件的
圆心角和圆周角? ∠BOC=600?
3、观察你所画图形,思考圆心与圆周角之间有几种位置关系?
B
C
O.
90°
∟
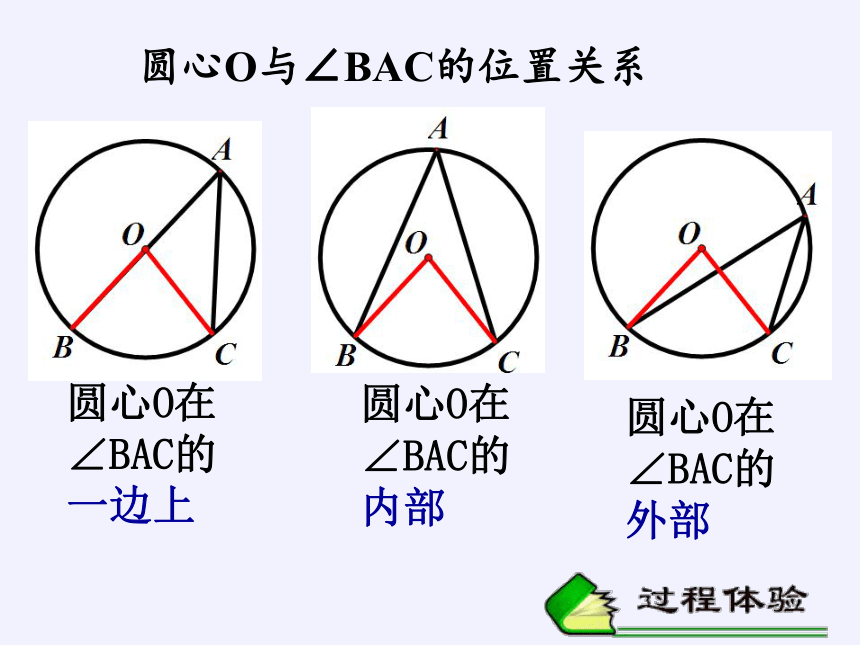
圆心O与∠BAC的位置关系
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
探究二:
∟
O
90°
B
A
C
A
⌒
120°
B
C
O
⌒
A
B
C
n°
O
你发现了什么?
45°
60°
如图,AB为⊙O的直径,∠BOC、∠BAC分别是所对的圆心角、圆周角,算一算图中∠BAC的度数.
已知:⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC。
A
O
B
C
∵ OA=OC
∴ ∠OCA=∠BAC
证明:
∵ ∠BOC是△AOC的外角
∴ ∠BOC=∠BAC+∠OCA
∴ ∠BOC=2∠BAC
即∠BAC= ∠BOC.
证一证
O
A
B
C
O
A
B
C
C
O
A
B
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
思考:当圆心O在∠BAC的内部或外部时,
还成立吗?
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
圆心O在∠BAC的外部
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
结论:
圆周角的度数等于它所对弧上的圆心角度数的一半。
=
=
=
思考:若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?
O
A
B
C
D
P
Q
1.圆周角的度数等于它所对弧上的圆心角度数的一半。(圆周角的度数等于它所对的弧的度数的一半)
圆周角定理:
O
B
C
A
D
E
2.同弧或等弧所对的圆周角相等。
例1、如图,点A、B、C、D在圆O上,点A与点D在点B、C所在直线的同侧,∠BAC= 35°,则(1)∠BDC= ,理由是 ;
(2)∠BOC= ,理由是 。
35°
70°
同弧所对的圆周角相等。
同弧所对的圆周角等于该弧所对的圆心角的一半。
三、个性展示
例2.如图,⊙O的弦AB、CD的延长线相交于点E,
∠AOD=150 ° , BC 为70°。求∠ABD、∠AED
的度数。
三、个性展示
?
?
150 °
35°
70°
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
比较∠BAC的∠BDC大小?
小明
小强
A
D
B
C
O
例1:站在点D的小强向后退了几步,退到了圆外,此时从射门角度大小考虑,小明A、小强D谁的位置射门更有利?
F
E
例3:如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC 与∠BDC的大小,并说明理由。
例题解析
小明
三、个性展示
例3:如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC 与∠BDC的大小,并说明理由。
解:∠BAC>∠BDC
∵∠BFC是△CDF的一个外角
∴∠BFC>∠BDC
∵∠BAC =∠BFC
∴∠BAC>∠BDC
(同弧所对的圆周角相等)
连接CF
A
D
B
C
O
F
E
变式:站在点D的小强向前进了几步,进到了圆内,仅从射门角度大小考虑,此时小明A、 小强D谁的位置射门更有利?
例题解析
小明
变式:如图,移动点D到圆内,其它条件不变,此时∠BAC与∠BDC的大小又如何?并说明理由。
延长BD交⊙O于点E,连接CE
∵∠BDC是△CDE的一个外角
∴∠BDC>∠BEC
∵∠BAC =∠BEC
∴∠BDC>∠BAC
解: ∠BDC>∠BAC。理由是:
(同弧所对的圆周角相等)
E
三、个性展示
1.如图,D是弧AC的中点,与∠ABD相等的角的个数是( ).
A.4个 B.3 个 C.2 个 D.1个
B
=
=
四、整合提升
2.如图,已知AB=AC=AD,∠CBD=2∠BDC,
∠BAC=42°,则∠ACD的度数为 .
四、整合提升
480
420
1、数学知识
(2)圆周角定理:
五、课堂小结
(1)圆周角的概念:
分类讨论
O
A
B
C
O
A
B
C
C
O
A
B
由特殊到一般
2、数学思想与方法
O
A
B
C
D
C
O
A
B
D
O
A
B
C
转化
由一般到特殊
2、数学思想与方法
E
化转
转化
转化思想
2、数学思想与方法
1.如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来:
六、反馈训练:
3.如图,∠1、∠2、∠3、∠4的大小关系是( ) A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3 <∠2 D.∠4<∠1<∠3=∠2
4.如图,已知圆心角∠AOC的度数为100 °,求圆周角∠ABC的度数.
5.在半径为r的圆中有一条长度为r的弦,则该弦所对的圆周角的度数是
6.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻。当甲带球到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)
7、如图,点A、B、C、D在⊙O上,∠ADC=∠BDC=60°.
(1).判断△ABC的形状,并说明理由.
(2).求证:AD+BD=CD
8、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
⌒
⌒
谢 谢
你喜欢踢足球吗?你知道足球队员之间踢球的关键是什么?
配合
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
比较∠BAC的∠BDC大小?
小明
小强
一、课前准备
初中数学九年级上册
(苏科版)
沭阳如东实验学校初三备课组
2.4 圆周角(1)
学习目标
1.掌握圆周角的概念
2.体验并掌握圆周角定理的探究过程
3.感悟圆周角定理中数学思想方法
.
把圆心角∠POQ的顶点移到点A、B1、B2、C处,形成了不同于圆心角的一些角,图中∠B1、∠B2的顶点位置有什么共同特征?
问题:
P
Q
O
A
B1
B2
C
圆周角的定义
O
B
C
A
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
⑴顶点在圆上
⑵角的两边和圆相交
特征:
二、合作探究
请大家画出一个错误的圆周角。
1.找找新朋友
①
.
②
.
③
.
⑤
.
④
.
——圆周角
2.图中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个
C
探究一:
2、量一量你所画的圆周角的度数,发现了什么?
同弧所对的圆周角相等
1、请在⊙O中, OB⊥OC,画出 所对的圆
心角和圆周角,你能画出多少个符合条件的
圆心角和圆周角? ∠BOC=600?
3、观察你所画图形,思考圆心与圆周角之间有几种位置关系?
B
C
O.
90°
∟
圆心O与∠BAC的位置关系
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
探究二:
∟
O
90°
B
A
C
A
⌒
120°
B
C
O
⌒
A
B
C
n°
O
你发现了什么?
45°
60°
如图,AB为⊙O的直径,∠BOC、∠BAC分别是所对的圆心角、圆周角,算一算图中∠BAC的度数.
已知:⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC。
A
O
B
C
∵ OA=OC
∴ ∠OCA=∠BAC
证明:
∵ ∠BOC是△AOC的外角
∴ ∠BOC=∠BAC+∠OCA
∴ ∠BOC=2∠BAC
即∠BAC= ∠BOC.
证一证
O
A
B
C
O
A
B
C
C
O
A
B
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
思考:当圆心O在∠BAC的内部或外部时,
还成立吗?
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
圆心O在∠BAC的外部
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
结论:
圆周角的度数等于它所对弧上的圆心角度数的一半。
=
=
=
思考:若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?
O
A
B
C
D
P
Q
1.圆周角的度数等于它所对弧上的圆心角度数的一半。(圆周角的度数等于它所对的弧的度数的一半)
圆周角定理:
O
B
C
A
D
E
2.同弧或等弧所对的圆周角相等。
例1、如图,点A、B、C、D在圆O上,点A与点D在点B、C所在直线的同侧,∠BAC= 35°,则(1)∠BDC= ,理由是 ;
(2)∠BOC= ,理由是 。
35°
70°
同弧所对的圆周角相等。
同弧所对的圆周角等于该弧所对的圆心角的一半。
三、个性展示
例2.如图,⊙O的弦AB、CD的延长线相交于点E,
∠AOD=150 ° , BC 为70°。求∠ABD、∠AED
的度数。
三、个性展示
?
?
150 °
35°
70°
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
比较∠BAC的∠BDC大小?
小明
小强
A
D
B
C
O
例1:站在点D的小强向后退了几步,退到了圆外,此时从射门角度大小考虑,小明A、小强D谁的位置射门更有利?
F
E
例3:如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC 与∠BDC的大小,并说明理由。
例题解析
小明
三、个性展示
例3:如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC 与∠BDC的大小,并说明理由。
解:∠BAC>∠BDC
∵∠BFC是△CDF的一个外角
∴∠BFC>∠BDC
∵∠BAC =∠BFC
∴∠BAC>∠BDC
(同弧所对的圆周角相等)
连接CF
A
D
B
C
O
F
E
变式:站在点D的小强向前进了几步,进到了圆内,仅从射门角度大小考虑,此时小明A、 小强D谁的位置射门更有利?
例题解析
小明
变式:如图,移动点D到圆内,其它条件不变,此时∠BAC与∠BDC的大小又如何?并说明理由。
延长BD交⊙O于点E,连接CE
∵∠BDC是△CDE的一个外角
∴∠BDC>∠BEC
∵∠BAC =∠BEC
∴∠BDC>∠BAC
解: ∠BDC>∠BAC。理由是:
(同弧所对的圆周角相等)
E
三、个性展示
1.如图,D是弧AC的中点,与∠ABD相等的角的个数是( ).
A.4个 B.3 个 C.2 个 D.1个
B
=
=
四、整合提升
2.如图,已知AB=AC=AD,∠CBD=2∠BDC,
∠BAC=42°,则∠ACD的度数为 .
四、整合提升
480
420
1、数学知识
(2)圆周角定理:
五、课堂小结
(1)圆周角的概念:
分类讨论
O
A
B
C
O
A
B
C
C
O
A
B
由特殊到一般
2、数学思想与方法
O
A
B
C
D
C
O
A
B
D
O
A
B
C
转化
由一般到特殊
2、数学思想与方法
E
化转
转化
转化思想
2、数学思想与方法
1.如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来:
六、反馈训练:
3.如图,∠1、∠2、∠3、∠4的大小关系是( ) A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3 <∠2 D.∠4<∠1<∠3=∠2
4.如图,已知圆心角∠AOC的度数为100 °,求圆周角∠ABC的度数.
5.在半径为r的圆中有一条长度为r的弦,则该弦所对的圆周角的度数是
6.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻。当甲带球到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)
7、如图,点A、B、C、D在⊙O上,∠ADC=∠BDC=60°.
(1).判断△ABC的形状,并说明理由.
(2).求证:AD+BD=CD
8、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
⌒
⌒
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
