人教版数学九年级上册:21.3实际问题与一元一次方程 第1课时 课件(含视频 共15张PPT)
文档属性
| 名称 | 人教版数学九年级上册:21.3实际问题与一元一次方程 第1课时 课件(含视频 共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
21.3
实际问题与一元二次方程
-------传播问题
1.经历从实际问题中抽象出一元二次方程的过程,体会方程是刻画现实世界的一个有效的数学模型。
2.了解列一元二次方程解应用题的一般步骤,掌握“传播问题”的基本数量关系,并能根据这些数量关系列方程解决问题。
3.体验利用数学知识解决生活实际的过程中获得的快乐,同时在合作交流中培养与人合作的团队精神。
学习目标
同
学
们
有
哪
些
启
发
呢
?
2020年1月24日到3月20日中国疫情地图变化
有1人得了流感,第一轮传染4个同学;第二轮传染中,这些人又每人传染了4名同学,经过两轮传染后,一共有几名同学被感染?
新课引入
传染源(人)
感染者(人)
总感染(人)
第一轮
第二轮
4
5
5
20
25
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
第1轮
第2轮
1
传染源
传染源
1
2
3
4
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
小明
第1轮
小明
1
2
x
???
第2轮
解:设每轮传染中平均一个人传染了x
个人
探索新知
传染源(人)
感染者(人)
总感染(人)
第一轮
第二轮
1
1+x
x
(1+x)x
1+x
1+x+(1+x)x=(1+x)2
x1=
,
x2=
解得:
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x
个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,
所以一定要进行检验.
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
探索新知
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
第三轮
探索新知
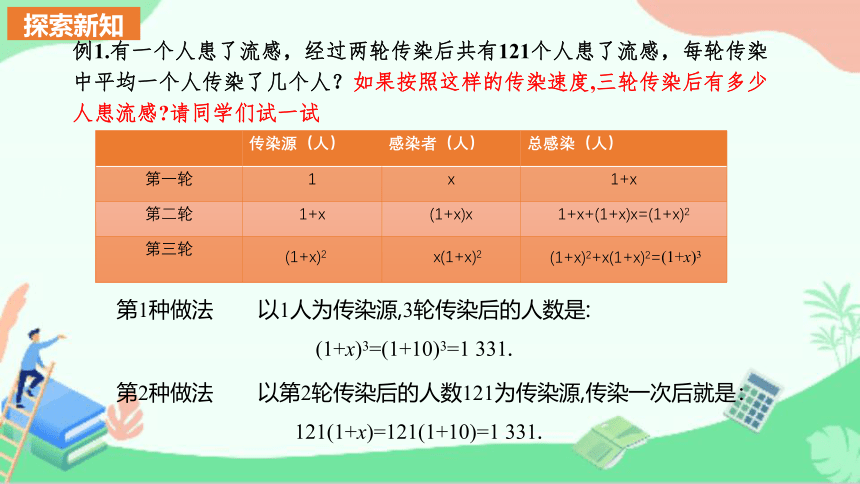
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?如果按照这样的传染速度,三轮传染后有多少人患流感?请同学们试一试
(1+x)2
x(1+x)2
(1+x)2+x(1+x)2=(1+x)3
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1
331.
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:
121(1+x)=121(1+10)=1
331.
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
第三轮
(1+x)2
x(1+x)2
(1+x)2+x(1+x)2=(1+x)3
第n轮
探索新知
如果按这样的传染速度,n
轮传染后有多少人患了流感?
(1+x)n-1
(1+x)n-1?x
(1+x)n
结论:经过n轮传染后共有
(1+x)n
人患流感.
对应练习:某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有
100
台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染
x
台电脑,则
1+x+x(1+x)=100
即(1+x)2=100
解得
x1=9
x2=-11(舍去)
∴x=9
答:每轮感染中平均每一台电脑会感染
9
台电脑
例2:某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则
1+x+x2=91
即
解得
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
对应练习.
有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为(
)
A.1+x+x(1+x)=73
B.1+x+x2=73
C.1+x2
=73
D.(1+x)2=73
B
1.在分析例2和例1中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
交流讨论
例3
细胞分裂问题
某种细胞细胞分裂时,每个细胞在每轮分裂中分成两个细胞.
(1)经过三轮分裂后细胞的个数是
.
(2)n轮分裂后,细胞的个数共是
.
8
2n
对应练习:
一种细胞,每经过20分钟分裂一次,每个细胞分裂成两个,一个细胞经过2小时能分裂成多少个?
解:(1)2小时=120分钟,
120÷20=6(次)
=64(个)
答:一个细胞经过2小时能分裂成64个
课后作业
1.必做题:课本P22第4题
2.选做题:课本P22第10题
21.3
实际问题与一元二次方程
-------传播问题
1.经历从实际问题中抽象出一元二次方程的过程,体会方程是刻画现实世界的一个有效的数学模型。
2.了解列一元二次方程解应用题的一般步骤,掌握“传播问题”的基本数量关系,并能根据这些数量关系列方程解决问题。
3.体验利用数学知识解决生活实际的过程中获得的快乐,同时在合作交流中培养与人合作的团队精神。
学习目标
同
学
们
有
哪
些
启
发
呢
?
2020年1月24日到3月20日中国疫情地图变化
有1人得了流感,第一轮传染4个同学;第二轮传染中,这些人又每人传染了4名同学,经过两轮传染后,一共有几名同学被感染?
新课引入
传染源(人)
感染者(人)
总感染(人)
第一轮
第二轮
4
5
5
20
25
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
第1轮
第2轮
1
传染源
传染源
1
2
3
4
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
小明
第1轮
小明
1
2
x
???
第2轮
解:设每轮传染中平均一个人传染了x
个人
探索新知
传染源(人)
感染者(人)
总感染(人)
第一轮
第二轮
1
1+x
x
(1+x)x
1+x
1+x+(1+x)x=(1+x)2
x1=
,
x2=
解得:
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x
个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,
所以一定要进行检验.
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
探索新知
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
第三轮
探索新知
例1.有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?如果按照这样的传染速度,三轮传染后有多少人患流感?请同学们试一试
(1+x)2
x(1+x)2
(1+x)2+x(1+x)2=(1+x)3
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1
331.
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:
121(1+x)=121(1+10)=1
331.
传染源(人)
感染者(人)
总感染(人)
第一轮
1
x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=(1+x)2
第三轮
(1+x)2
x(1+x)2
(1+x)2+x(1+x)2=(1+x)3
第n轮
探索新知
如果按这样的传染速度,n
轮传染后有多少人患了流感?
(1+x)n-1
(1+x)n-1?x
(1+x)n
结论:经过n轮传染后共有
(1+x)n
人患流感.
对应练习:某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有
100
台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染
x
台电脑,则
1+x+x(1+x)=100
即(1+x)2=100
解得
x1=9
x2=-11(舍去)
∴x=9
答:每轮感染中平均每一台电脑会感染
9
台电脑
例2:某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则
1+x+x2=91
即
解得
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
对应练习.
有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为(
)
A.1+x+x(1+x)=73
B.1+x+x2=73
C.1+x2
=73
D.(1+x)2=73
B
1.在分析例2和例1中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
交流讨论
例3
细胞分裂问题
某种细胞细胞分裂时,每个细胞在每轮分裂中分成两个细胞.
(1)经过三轮分裂后细胞的个数是
.
(2)n轮分裂后,细胞的个数共是
.
8
2n
对应练习:
一种细胞,每经过20分钟分裂一次,每个细胞分裂成两个,一个细胞经过2小时能分裂成多少个?
解:(1)2小时=120分钟,
120÷20=6(次)
=64(个)
答:一个细胞经过2小时能分裂成64个
课后作业
1.必做题:课本P22第4题
2.选做题:课本P22第10题
同课章节目录
