人教新课标数学六年级下册《圆柱的体积》ppt课件
文档属性
| 名称 | 人教新课标数学六年级下册《圆柱的体积》ppt课件 |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-28 20:34:49 | ||
图片预览



文档简介
(共26张PPT)
圆柱的体积
教学目标
1. 结合实际让大家探索并掌握圆柱体积的计算方法,能正确运用公式解决简单的实际问题。
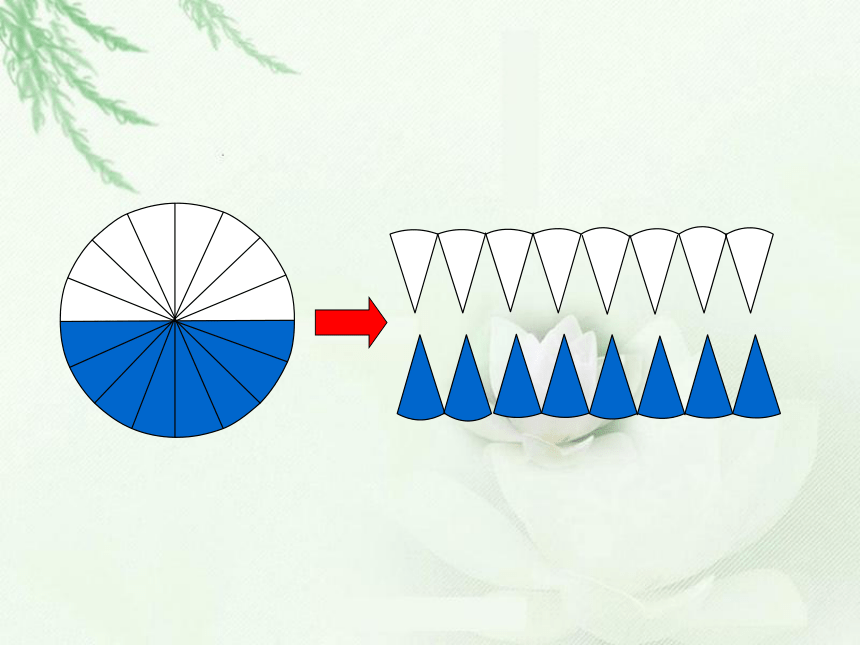
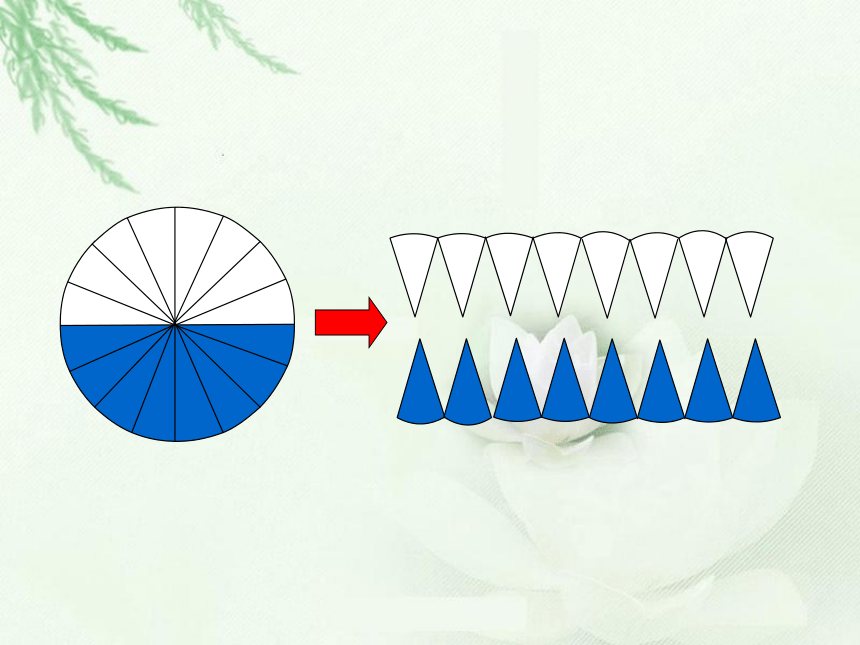
2. 让大家经历观察、猜想、验证等数学活动过程,渗透“转化”、“极限”等数学思想,体验数学研究的方法。
长
v
=a b h
v
3
正
=a
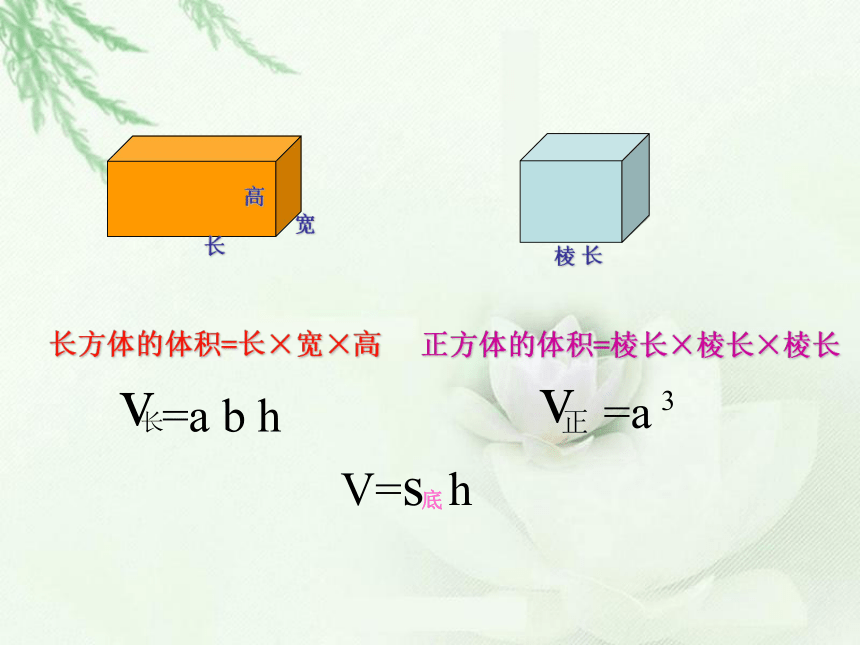
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
V=s h
底
长
宽
高
棱 长
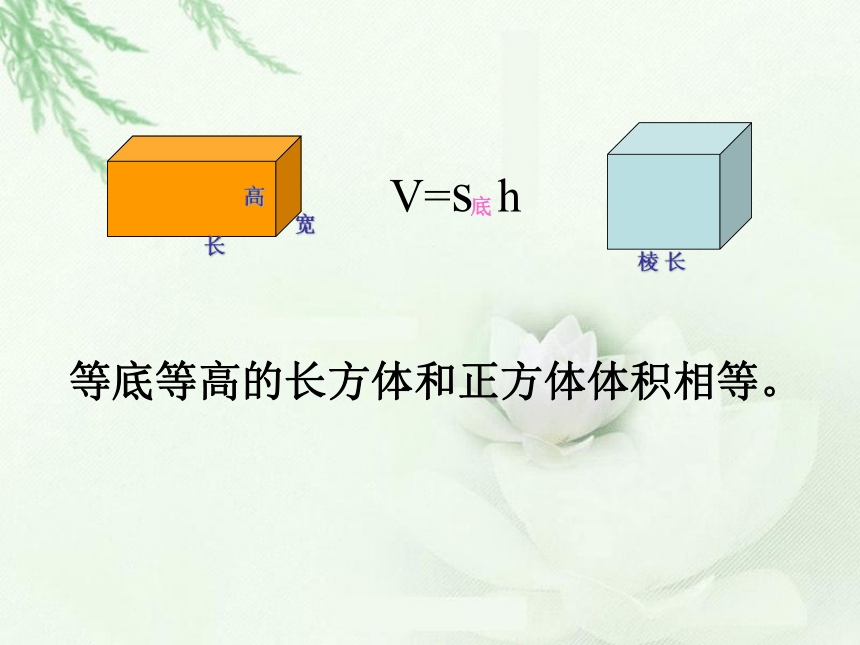
等底等高的长方体和正方体体积相等。
长方体体积=底面积×高
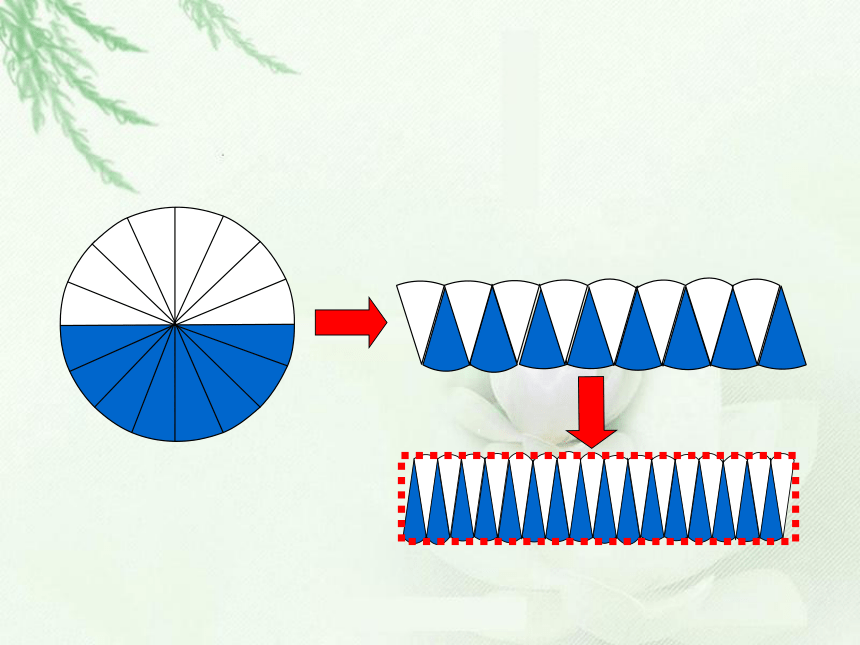
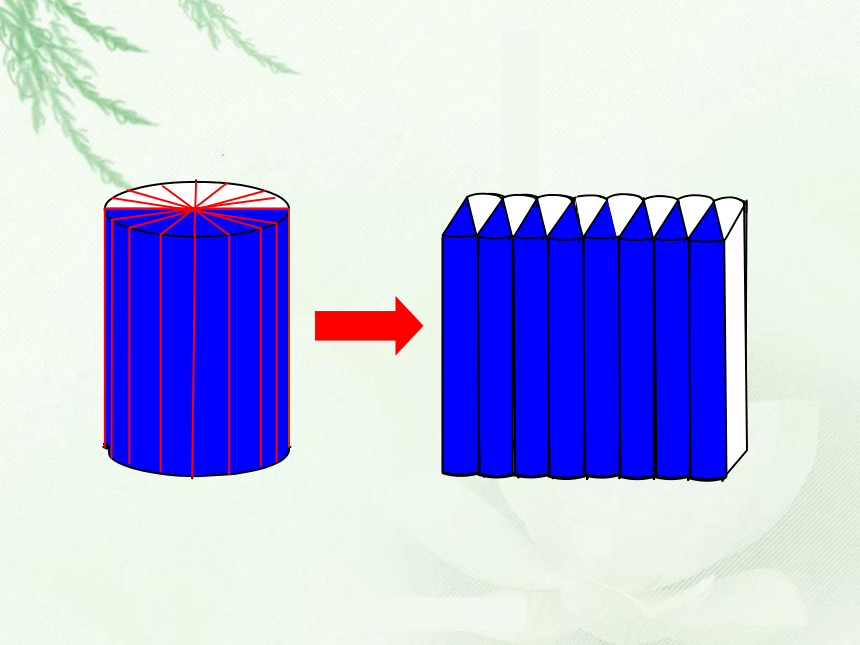
圆柱体积=底面积×高
高
底面积
高
V=sh
一根圆柱形木料,底面积是75平方厘米,长90厘米。它的体积是多少?
圆柱体积=底面积×高
75×90=6750(立方厘米)
答:它的体积是6750立方厘米。
讨论
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
讨论
(1)已知圆的半径和高:
(2)已知圆的直径和高:
(3)已知圆的周长和高:
V=∏r2h
V=∏( )2h
d
2
V=∏(C÷d÷2 )2h
圆柱形水桶内所盛水的体积,就叫做这个圆柱形容器的容积。
下面这个杯子能不能装下这袋奶 (杯子的数据是从里面测量得到的。)
8cm
10cm
498ml
先要计算出杯子的容积。
杯子的底面积: 3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(c㎡)
2
2
杯子的容积: 50.24×10
=502.4(ml)
502.4ml>498ml
答:这个杯子能装下这袋奶。
判断正误,对的画“√”,错误的画“×”。
(1)圆柱体的底面积越大,它的体积越大。( )
(2)圆柱体的高越长,它的体积越大。( )
(3)圆柱体的体积与长方体的体积相等。( )
(4)圆柱体的底面直径和高可以相等。( )
×
×
×
√
求各圆柱的体积。
2厘米
2厘米
4分米
10分米
0.8米
0.5分米
一根圆柱形钢材,底面积是20平方厘米,高是1.5米。它的体积是多少?
圆柱体积=底面积×高
1.5米=150厘米
20×150=3000(立方厘米)
答:它的体积是3000立方厘米。
一根圆柱形柱子,底面半径是0.4米,高是5米。它的体积是多少?
答:它的体积是2.512立方米。
3.14 ×0.42×5=2.512(立方米)
(1)水桶的底面积:3.14×( )2=314(cm2)
(2)水桶的容积: 314×13=4082(cm3)
20
2
容积?
量得底面直径是20厘米,高是13厘米
3分米
4分米
(1)水桶的底面积:3.14×( )2=7.065(dm2)
(2)水桶的容积: 7.065×4=28.26(L)
3
2
一个圆柱形水桶,从桶内量底面直径是3分米,高是4分米,这个水桶的容积是多少升
一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少
谢 谢!
圆柱的体积
教学目标
1. 结合实际让大家探索并掌握圆柱体积的计算方法,能正确运用公式解决简单的实际问题。
2. 让大家经历观察、猜想、验证等数学活动过程,渗透“转化”、“极限”等数学思想,体验数学研究的方法。
长
v
=a b h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
V=s h
底
长
宽
高
棱 长
等底等高的长方体和正方体体积相等。
长方体体积=底面积×高
圆柱体积=底面积×高
高
底面积
高
V=sh
一根圆柱形木料,底面积是75平方厘米,长90厘米。它的体积是多少?
圆柱体积=底面积×高
75×90=6750(立方厘米)
答:它的体积是6750立方厘米。
讨论
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
讨论
(1)已知圆的半径和高:
(2)已知圆的直径和高:
(3)已知圆的周长和高:
V=∏r2h
V=∏( )2h
d
2
V=∏(C÷d÷2 )2h
圆柱形水桶内所盛水的体积,就叫做这个圆柱形容器的容积。
下面这个杯子能不能装下这袋奶 (杯子的数据是从里面测量得到的。)
8cm
10cm
498ml
先要计算出杯子的容积。
杯子的底面积: 3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(c㎡)
2
2
杯子的容积: 50.24×10
=502.4(ml)
502.4ml>498ml
答:这个杯子能装下这袋奶。
判断正误,对的画“√”,错误的画“×”。
(1)圆柱体的底面积越大,它的体积越大。( )
(2)圆柱体的高越长,它的体积越大。( )
(3)圆柱体的体积与长方体的体积相等。( )
(4)圆柱体的底面直径和高可以相等。( )
×
×
×
√
求各圆柱的体积。
2厘米
2厘米
4分米
10分米
0.8米
0.5分米
一根圆柱形钢材,底面积是20平方厘米,高是1.5米。它的体积是多少?
圆柱体积=底面积×高
1.5米=150厘米
20×150=3000(立方厘米)
答:它的体积是3000立方厘米。
一根圆柱形柱子,底面半径是0.4米,高是5米。它的体积是多少?
答:它的体积是2.512立方米。
3.14 ×0.42×5=2.512(立方米)
(1)水桶的底面积:3.14×( )2=314(cm2)
(2)水桶的容积: 314×13=4082(cm3)
20
2
容积?
量得底面直径是20厘米,高是13厘米
3分米
4分米
(1)水桶的底面积:3.14×( )2=7.065(dm2)
(2)水桶的容积: 7.065×4=28.26(L)
3
2
一个圆柱形水桶,从桶内量底面直径是3分米,高是4分米,这个水桶的容积是多少升
一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少
谢 谢!
