苏科版九年级上册 数学 课件 2.4 圆周角(17张PPT)
文档属性
| 名称 | 苏科版九年级上册 数学 课件 2.4 圆周角(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 335.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 21:05:38 | ||
图片预览


文档简介
2.4 圆周角
与圆有关的角
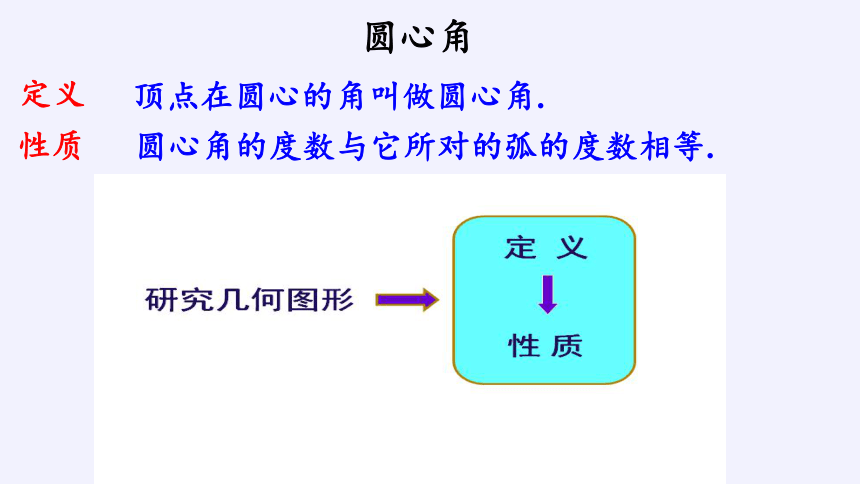
活动一:温故探新
性质
圆心角的度数与它所对的弧的度数相等.
O
B
C
定义
顶点在圆心的角叫做圆心角.
圆心角
·
C
O
B
A
·
C
O
A
B
·
C
O
B
A
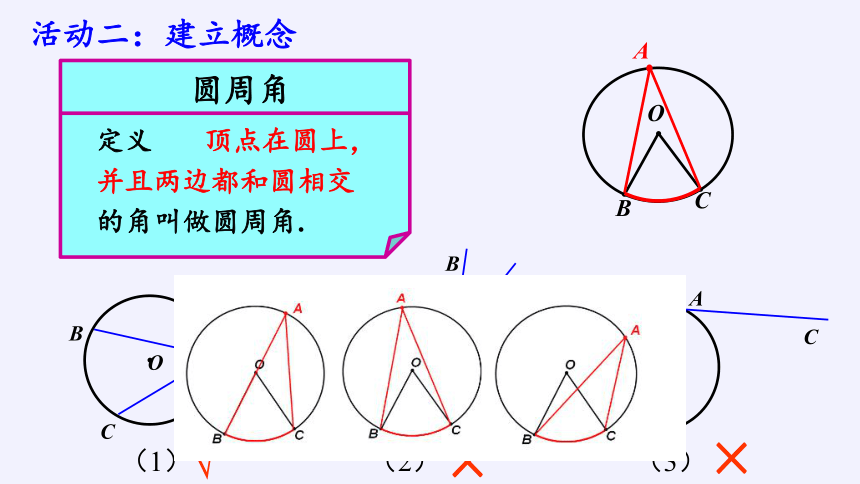
(2)
(1)
(3)
×
×
√
O
B
C
A
圆周角
定义
顶点在圆上,
并且两边都和圆相交
的角叫做圆周角.
活动二:建立概念
A
O
C
B
1
2
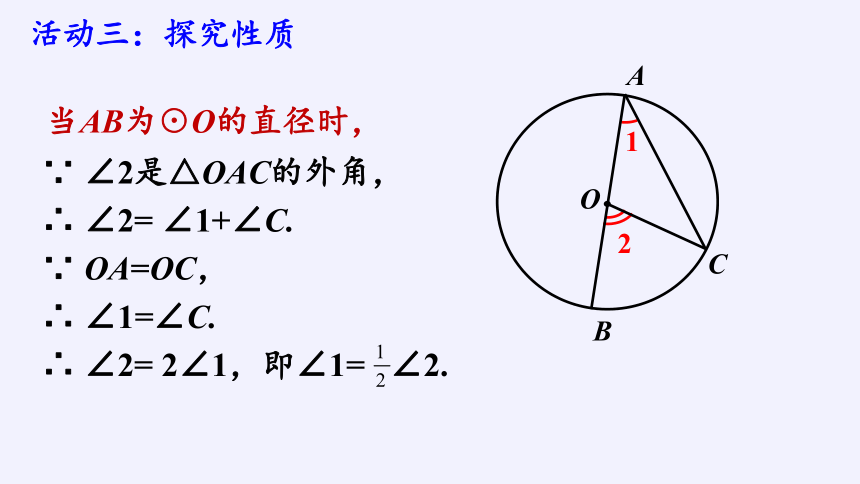
∵ ∠2是△OAC的外角,
∴ ∠2= ∠1+∠C.
∵ OA=OC,
∴ ∠1=∠C.
∴ ∠2= 2∠1,即∠1= ∠2.
当AB为☉O的直径时,
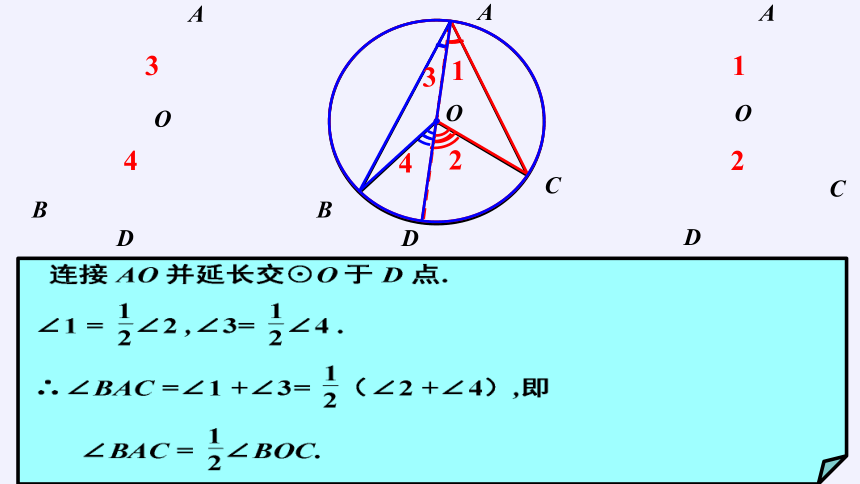
活动三:探究性质
A
O
D
C
B
A
O
D
C
A
O
D
B
3
2
4
1
2
4
1
3
D
B
A
O
C
1
2
3
4
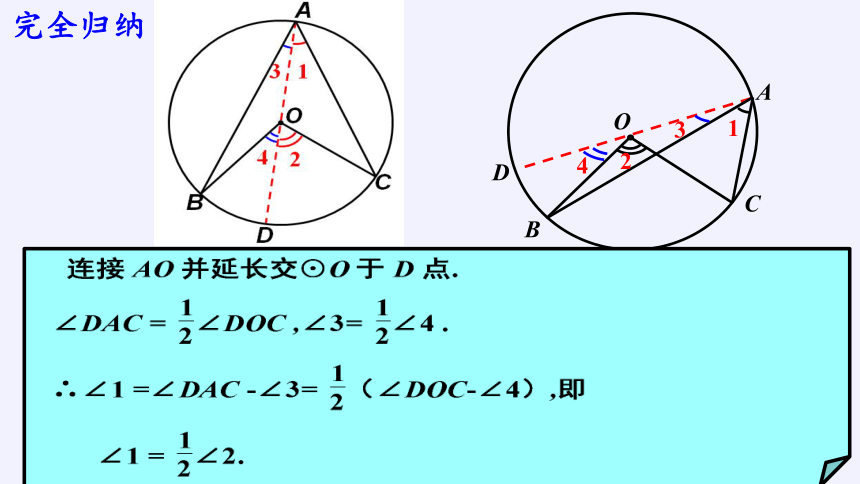
完全归纳
推理思考
如图,点A、B、C、D 、E、F、G均为
☉O上的点,AB与CD是等弧,则∠E与∠F
的大小关系如何?
∠E与∠G的大小关系呢?
1.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.填空:
(2)∠2=∠ ;
(1)∠1=∠ ;
(3)∠3=∠ ;
(4)∠5=∠ .
4
7
6
8
活动四:学以致用
2.如图,点A、B、C、D在
☉O上,点A与点D在点B、C所
在直线的同侧,∠BAC=35?.
(1)∠BDC= ?,理由是 ;
(2)∠BOC= ?,理由是 .
35
70
同弧所对的圆周角相等
同弧所对的圆周角等于该
弧所对的圆心角的一半
3.如图,在⊙O中,弦AB、CD相交于点E,∠BAC=45?,∠AED=75?. (1)求∠ABD的度数;
(2)连接AD, 若AD=2,求⊙O的半径长.
45?
75?
30?
60?
B
C
A
D
E
与圆有关的角除了圆心角、圆周角还有其
它的角,比较∠A、∠D、∠E的大小关系,你
有什么发现?能说明你的结论吗?
D’
E’
活动五:思维拓展
活动六:反思提升
作业:
2.思考探索:给你一张圆形纸片,你有哪些方法能找出它的圆心位置?
1.课本第122页习题5.3第1,2,4,5题.
详见讲义(下页).
(一)必做题
(二)选做题
目标检测
3.在⊙O中, BC为弦,∠BOC=100?,则弦BC所对的圆周角的度数是 .
1.如左图,OA、OB、OC都是⊙O的半径,∠AOB = 2∠BOC. 请说明∠ACB = 2∠BAC.
2. 如右图,在⊙O中,BC=2DE,∠BOC=84°,求∠A的度数.
4.如图,一个海湾在AB范围内有暗礁,C是AB上一点,当船只位于AB外侧时 ,其所在位置P与两个灯塔A、B形成视角∠APB,请你比较∠APB与∠ACB的大小,并说明理由. (提示:可延长AC交PB于点D)
回归生活
海
湾
D
谢 谢
与圆有关的角
活动一:温故探新
性质
圆心角的度数与它所对的弧的度数相等.
O
B
C
定义
顶点在圆心的角叫做圆心角.
圆心角
·
C
O
B
A
·
C
O
A
B
·
C
O
B
A
(2)
(1)
(3)
×
×
√
O
B
C
A
圆周角
定义
顶点在圆上,
并且两边都和圆相交
的角叫做圆周角.
活动二:建立概念
A
O
C
B
1
2
∵ ∠2是△OAC的外角,
∴ ∠2= ∠1+∠C.
∵ OA=OC,
∴ ∠1=∠C.
∴ ∠2= 2∠1,即∠1= ∠2.
当AB为☉O的直径时,
活动三:探究性质
A
O
D
C
B
A
O
D
C
A
O
D
B
3
2
4
1
2
4
1
3
D
B
A
O
C
1
2
3
4
完全归纳
推理思考
如图,点A、B、C、D 、E、F、G均为
☉O上的点,AB与CD是等弧,则∠E与∠F
的大小关系如何?
∠E与∠G的大小关系呢?
1.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.填空:
(2)∠2=∠ ;
(1)∠1=∠ ;
(3)∠3=∠ ;
(4)∠5=∠ .
4
7
6
8
活动四:学以致用
2.如图,点A、B、C、D在
☉O上,点A与点D在点B、C所
在直线的同侧,∠BAC=35?.
(1)∠BDC= ?,理由是 ;
(2)∠BOC= ?,理由是 .
35
70
同弧所对的圆周角相等
同弧所对的圆周角等于该
弧所对的圆心角的一半
3.如图,在⊙O中,弦AB、CD相交于点E,∠BAC=45?,∠AED=75?. (1)求∠ABD的度数;
(2)连接AD, 若AD=2,求⊙O的半径长.
45?
75?
30?
60?
B
C
A
D
E
与圆有关的角除了圆心角、圆周角还有其
它的角,比较∠A、∠D、∠E的大小关系,你
有什么发现?能说明你的结论吗?
D’
E’
活动五:思维拓展
活动六:反思提升
作业:
2.思考探索:给你一张圆形纸片,你有哪些方法能找出它的圆心位置?
1.课本第122页习题5.3第1,2,4,5题.
详见讲义(下页).
(一)必做题
(二)选做题
目标检测
3.在⊙O中, BC为弦,∠BOC=100?,则弦BC所对的圆周角的度数是 .
1.如左图,OA、OB、OC都是⊙O的半径,∠AOB = 2∠BOC. 请说明∠ACB = 2∠BAC.
2. 如右图,在⊙O中,BC=2DE,∠BOC=84°,求∠A的度数.
4.如图,一个海湾在AB范围内有暗礁,C是AB上一点,当船只位于AB外侧时 ,其所在位置P与两个灯塔A、B形成视角∠APB,请你比较∠APB与∠ACB的大小,并说明理由. (提示:可延长AC交PB于点D)
回归生活
海
湾
D
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
