苏科版九年级上册 数学 课件 2.2 圆的对称性(25张PPT)
文档属性
| 名称 | 苏科版九年级上册 数学 课件 2.2 圆的对称性(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 534.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 21:10:55 | ||
图片预览

文档简介
2.2 圆的对称性
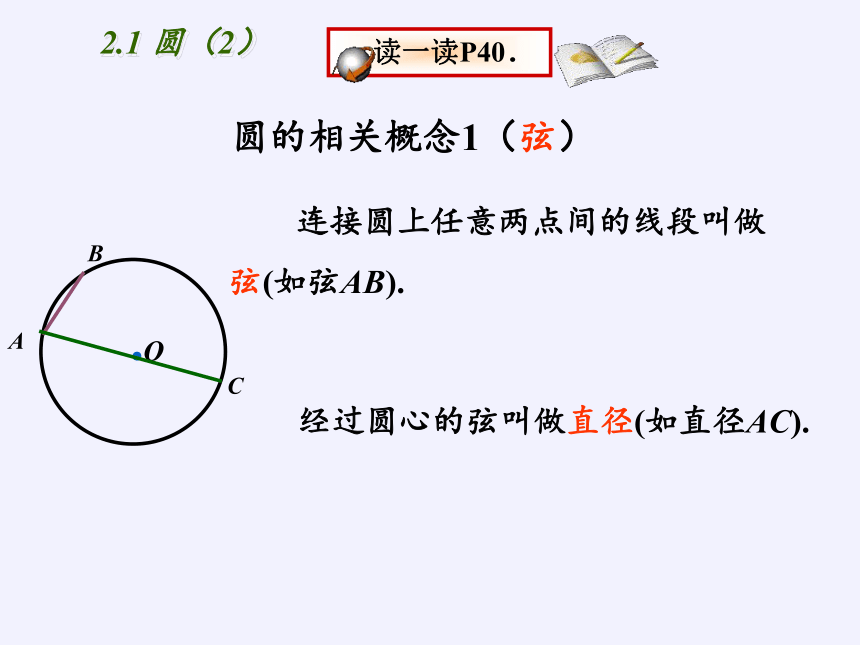
2.1 圆(2)
圆的相关概念1(弦)
连接圆上任意两点间的线段叫做弦(如弦AB).
●O
经过圆心的弦叫做直径(如直径AC).
A
B
C
读一读P40.
●
●
●
●
●
A
B
O
D
C
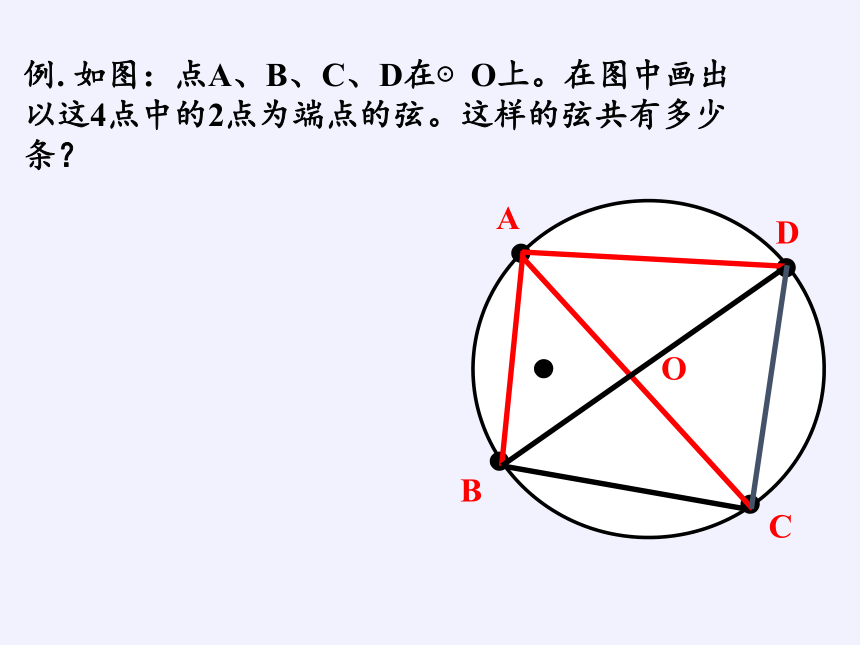
例. 如图:点A、B、C、D在⊙O上。在图中画出以这4点中的2点为端点的弦。这样的弦共有多少条?
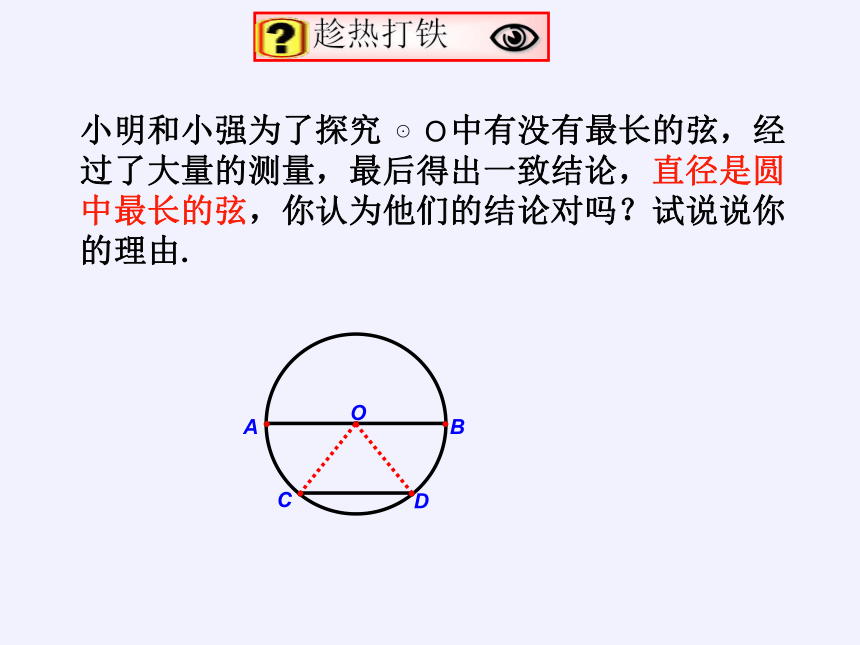
小明和小强为了探究 中有没有最长的弦,经过了大量的测量,最后得出一致结论,直径是圆中最长的弦,你认为他们的结论对吗?试说说你的理由.
⊙O
趁热打铁
?
2.1 圆(2)
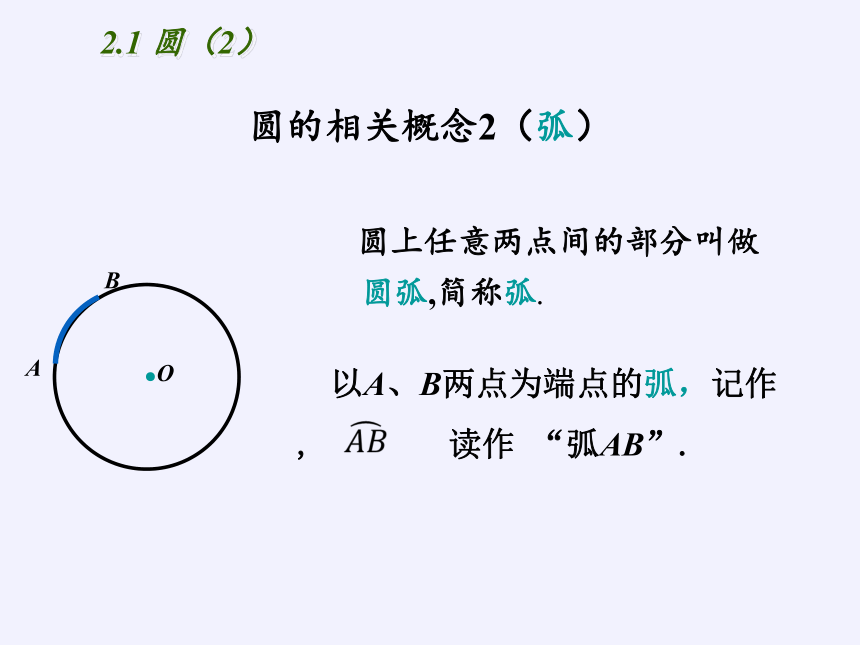
圆的相关概念2(弧)
圆上任意两点间的部分叫做
●O
A
B
以A、B两点为端点的弧,记作 , 读作 “弧AB”.
圆弧,简称弧.
●
A
B
C
O
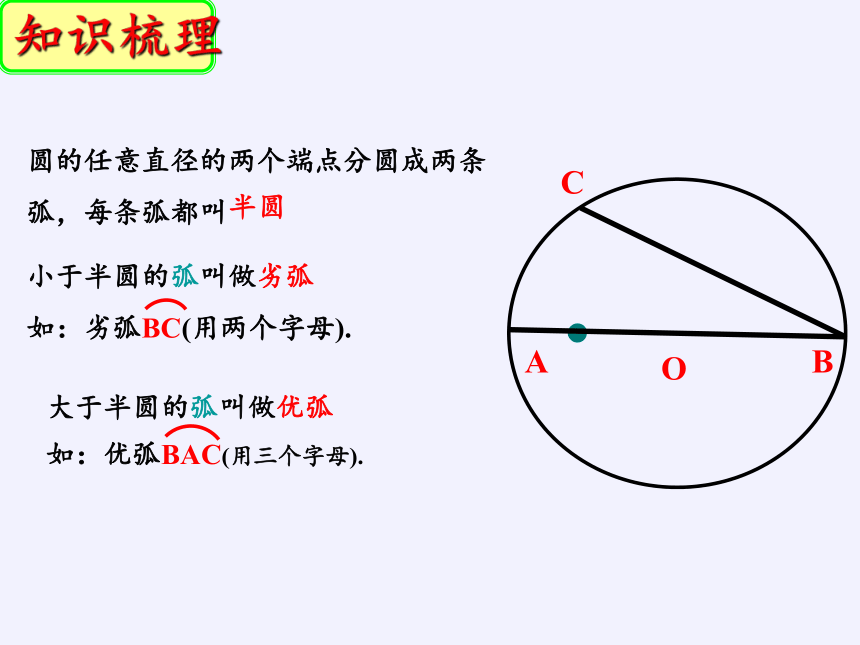
小于半圆的弧叫做劣弧
如:劣弧BC(用两个字母).
圆的任意直径的两个端点分圆成两条弧,每条弧都叫
知识梳理
大于半圆的弧叫做优弧
如:优弧BAC(用三个字母).
半圆
●
O
B
C
A
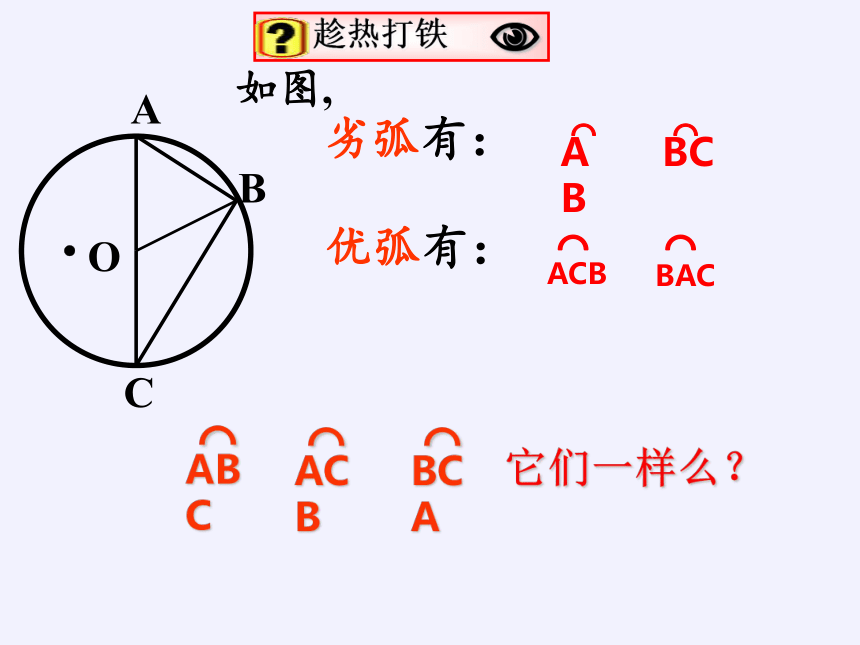
如图,
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
劣弧有:
优弧有:
⌒
ACB
⌒
BAC
趁热打铁
?
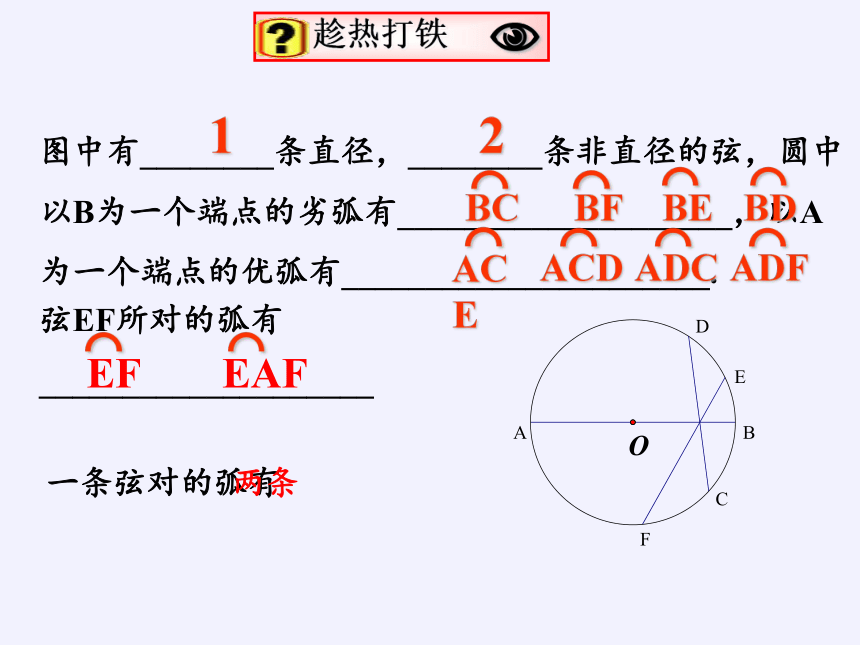
图中有________条直径,________条非直径的弦,圆中以B为一个端点的劣弧有____________________,以A为一个端点的优弧有______________________.
趁热打铁
?
弦EF所对的弧有____________________
一条弦对的弧有
⌒
ACE
1
2
⌒
⌒
⌒
⌒
ACD
ADC
ADF
⌒
⌒
⌒
BC
BF
BE
BD
⌒
⌒
EF
EAF
F
E
D
C
B
A
O
两条
2.1 圆(2)
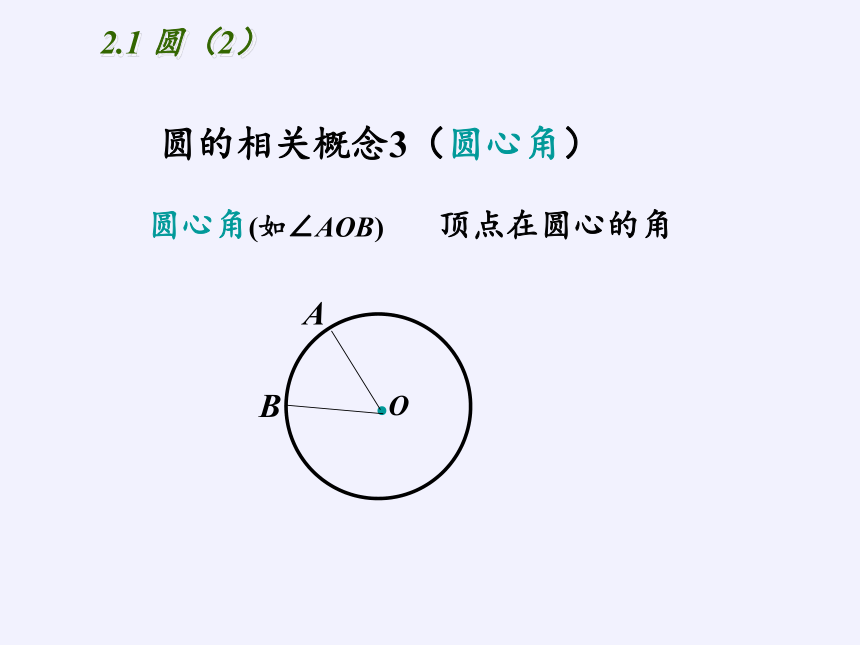
顶点在圆心的角
●O
A
B
圆的相关概念3(圆心角)
圆心角(如∠AOB)
2.1 圆(2)
例1.如图,AB是⊙O的直径,C是⊙O上一点,∠BAC与∠BOC有怎样的数量关系?
2.1 圆(2)
圆的相关概念4(同心圆)
圆心相同,半径不相等的两个圆
O
同心圆
2.1 圆(2)
圆的相关概念5(等圆)
能够互相重合的两个圆叫做
等圆
同心圆
等圆
同圆或等圆的半径 .
在同圆或等圆中,能够互相重合的弧叫 .
圆心相同,半径不同
能够互相重合的圆
在大小不等的两个圆中,存不存在等弧?
相等
等弧
1.(判断正误?)
(1)弦是直径;
(4)半圆是弧,但弧不一定是半圆;
(2)直径是最长的弦;
(3) 半圆是最长的弧;
(5)若P是⊙O内一点,过P点的最长的弦有一条.
慧眼识珠
?
1. 判断正误?)
(10)半径相等的两个半圆是等弧;
(11)同一条弦所对两条弧一定是一 条优弧一条劣弧.
(8)面积相等的两个圆是等圆;
(9)长度相等的两条弧是等弧;
(6)圆心相同,半径相等的两个圆是同心圆;
(7)半径相等的两个圆是等圆;
慧眼识珠
?
●
例1.(1)在图中,画出⊙O的两条直径
(2)依次连接这两条直径的端点,得一个四边形。判断这个四边形的形状,并说明理由
A
B
C
D
O
2.1 圆(2)
例2 已知:如图,点A、B和点C、D分别在同心圆上.且∠AOB=∠COD.∠C与∠D相等吗?为什么?
1.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C。如果BC=OE, ∠C=40°,求∠ EOA的度数.
知识应用
2.如图,⊙O中,直径MN=10 ,正方形ABCD四个顶点分别在半径OM、OP以及⊙O上,并且∠POM = 45°,求AB的长.
?
?
?
?
?
2.1 圆(2)
拓展探究
1.如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(1)求证:四边形OGCH是平行四边形;
2.1 圆(2)
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.
2.1 圆(2)
总结
通过今天的学习,你能谈谈你的收获和困惑,对圆有什么新的认识吗?
2.1 圆(2)
课后作业
课本P41-42第1、2、3.
2.1 圆(2)
谢 谢
2.1 圆(2)
圆的相关概念1(弦)
连接圆上任意两点间的线段叫做弦(如弦AB).
●O
经过圆心的弦叫做直径(如直径AC).
A
B
C
读一读P40.
●
●
●
●
●
A
B
O
D
C
例. 如图:点A、B、C、D在⊙O上。在图中画出以这4点中的2点为端点的弦。这样的弦共有多少条?
小明和小强为了探究 中有没有最长的弦,经过了大量的测量,最后得出一致结论,直径是圆中最长的弦,你认为他们的结论对吗?试说说你的理由.
⊙O
趁热打铁
?
2.1 圆(2)
圆的相关概念2(弧)
圆上任意两点间的部分叫做
●O
A
B
以A、B两点为端点的弧,记作 , 读作 “弧AB”.
圆弧,简称弧.
●
A
B
C
O
小于半圆的弧叫做劣弧
如:劣弧BC(用两个字母).
圆的任意直径的两个端点分圆成两条弧,每条弧都叫
知识梳理
大于半圆的弧叫做优弧
如:优弧BAC(用三个字母).
半圆
●
O
B
C
A
如图,
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
劣弧有:
优弧有:
⌒
ACB
⌒
BAC
趁热打铁
?
图中有________条直径,________条非直径的弦,圆中以B为一个端点的劣弧有____________________,以A为一个端点的优弧有______________________.
趁热打铁
?
弦EF所对的弧有____________________
一条弦对的弧有
⌒
ACE
1
2
⌒
⌒
⌒
⌒
ACD
ADC
ADF
⌒
⌒
⌒
BC
BF
BE
BD
⌒
⌒
EF
EAF
F
E
D
C
B
A
O
两条
2.1 圆(2)
顶点在圆心的角
●O
A
B
圆的相关概念3(圆心角)
圆心角(如∠AOB)
2.1 圆(2)
例1.如图,AB是⊙O的直径,C是⊙O上一点,∠BAC与∠BOC有怎样的数量关系?
2.1 圆(2)
圆的相关概念4(同心圆)
圆心相同,半径不相等的两个圆
O
同心圆
2.1 圆(2)
圆的相关概念5(等圆)
能够互相重合的两个圆叫做
等圆
同心圆
等圆
同圆或等圆的半径 .
在同圆或等圆中,能够互相重合的弧叫 .
圆心相同,半径不同
能够互相重合的圆
在大小不等的两个圆中,存不存在等弧?
相等
等弧
1.(判断正误?)
(1)弦是直径;
(4)半圆是弧,但弧不一定是半圆;
(2)直径是最长的弦;
(3) 半圆是最长的弧;
(5)若P是⊙O内一点,过P点的最长的弦有一条.
慧眼识珠
?
1. 判断正误?)
(10)半径相等的两个半圆是等弧;
(11)同一条弦所对两条弧一定是一 条优弧一条劣弧.
(8)面积相等的两个圆是等圆;
(9)长度相等的两条弧是等弧;
(6)圆心相同,半径相等的两个圆是同心圆;
(7)半径相等的两个圆是等圆;
慧眼识珠
?
●
例1.(1)在图中,画出⊙O的两条直径
(2)依次连接这两条直径的端点,得一个四边形。判断这个四边形的形状,并说明理由
A
B
C
D
O
2.1 圆(2)
例2 已知:如图,点A、B和点C、D分别在同心圆上.且∠AOB=∠COD.∠C与∠D相等吗?为什么?
1.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C。如果BC=OE, ∠C=40°,求∠ EOA的度数.
知识应用
2.如图,⊙O中,直径MN=10 ,正方形ABCD四个顶点分别在半径OM、OP以及⊙O上,并且∠POM = 45°,求AB的长.
?
?
?
?
?
2.1 圆(2)
拓展探究
1.如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(1)求证:四边形OGCH是平行四边形;
2.1 圆(2)
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.
2.1 圆(2)
总结
通过今天的学习,你能谈谈你的收获和困惑,对圆有什么新的认识吗?
2.1 圆(2)
课后作业
课本P41-42第1、2、3.
2.1 圆(2)
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
