苏科版九年级上册 数学 课件 3.4 方差(29张PPT)
文档属性
| 名称 | 苏科版九年级上册 数学 课件 3.4 方差(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 774.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 00:00:00 | ||
图片预览






文档简介
3.4
方差
复习回忆
1.什么是一组数据的极差?
极差反映了这组数据哪方面的特征?
答:
一组数据中的最大值减去最小值所得的差叫
做这组数据的极差,极差反映的是这组数据
的变化范围或变化幅度.
2、样本9.9,10.3,10.3,9.9,10.1的极差是
.
3、一组数据3、-1、0、2、x的极差是5,
且x为自然数,则x=
.
老师的烦恼
?
两个同学本学期五次测验的数学成绩分别如下:(单位:分)
假如要数学竞赛了,老师要从甲、乙两名同学中挑选一个参加。若你是老师,你认为挑选哪一位比较适宜?
甲
85
90
90
90
95
乙
95
85
95
85
90
创境引入
⑶
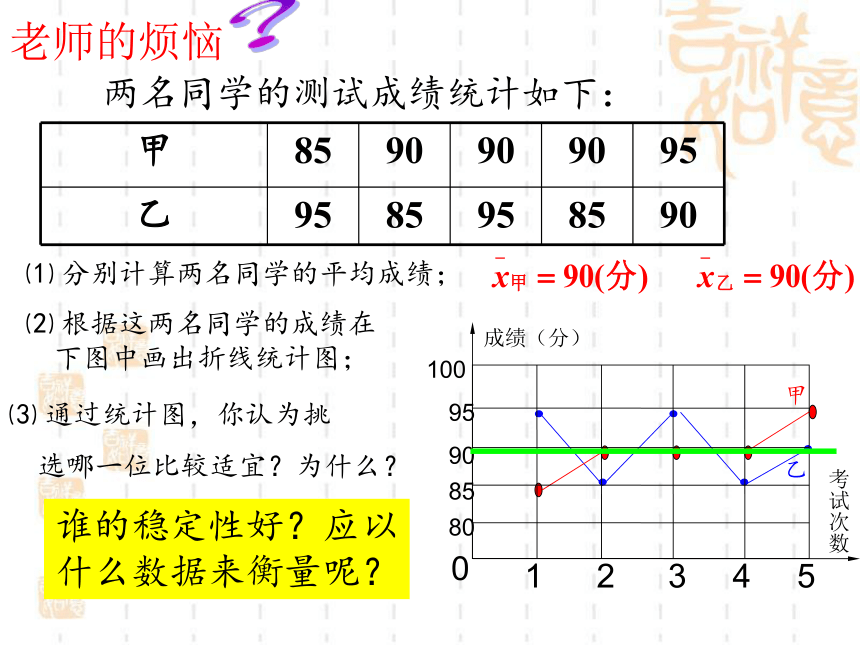
通过统计图,你认为挑
选哪一位比较适宜?为什么?
⑴
分别计算两名同学的平均成绩;
两名同学的测试成绩统计如下:
80
85
90
95
100
成绩(分)
0
1
2
3
4
5
考试次数
老师的烦恼
?
甲
85
90
90
90
95
乙
95
85
95
85
90
甲
乙
⑵
根据这两名同学的成绩在
下图中画出折线统计图;
谁的稳定性好?应以什么数据来衡量呢?
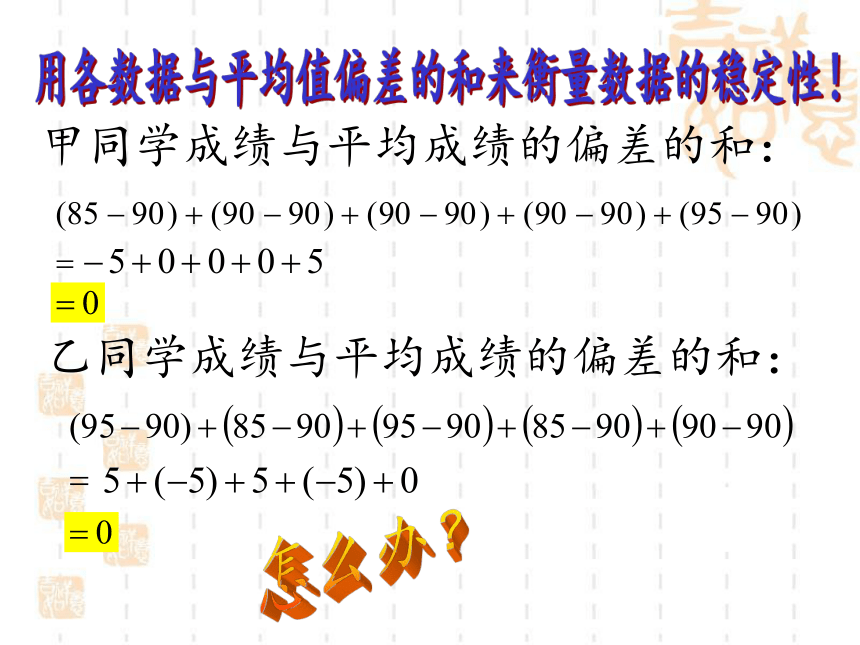
用各数据与平均值偏差的和来衡量数据的稳定性!
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
怎么办?
用偏差的平方和来衡量数据的稳定性!
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
50
100
老师的烦恼
?
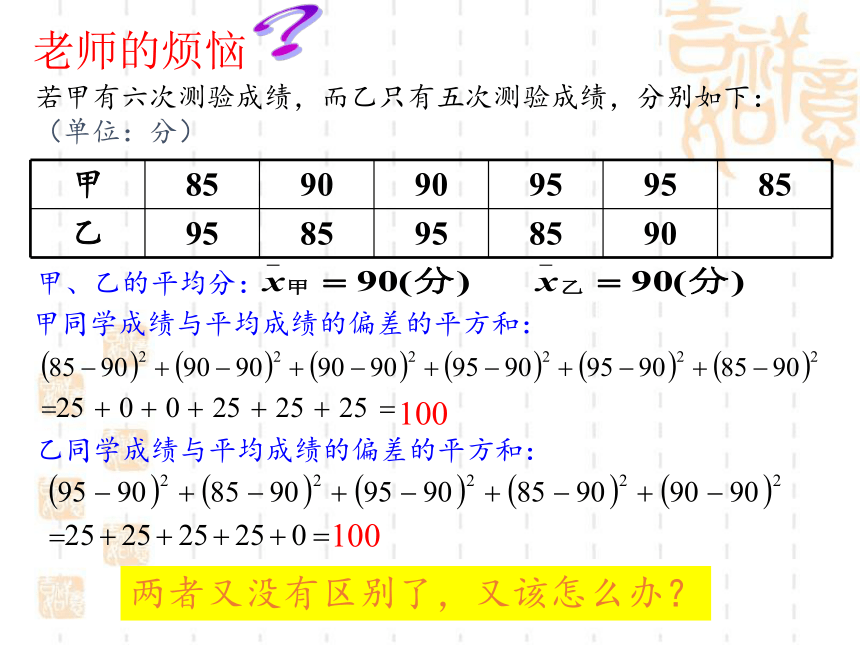
若甲有六次测验成绩,而乙只有五次测验成绩,分别如下:
(单位:分)
甲
85
90
90
95
95
85
乙
95
85
95
85
90
甲同学成绩与平均成绩的偏差的平方和:
100
乙同学成绩与平均成绩的偏差的平方和:
100
两者又没有区别了,又该怎么办?
甲、乙的平均分:
想一想
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性
16.7
20
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2
、…
(xn-x)2
,那么我们用它们的平均数,即用
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2=
[(x1-x)2+
(x2-x)2
+…+
(xn-x)2
]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,
平方后,再平均”.
定义
1、样本方差的作用是(
)
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、
在样本方差的计算公式
数字10
表示
,数字20表示
.
2、样本5、6、7、8、9的方差是
.
练习
D
2
样本平均数
样本容量
4、计算下列各组数据的方差:
(1)6
6
6
6
6
6
6;
(2)5
5
6
6
6
7
7;
(3)3
3
4
6
8
9
9;
(2)3
3
3
6
9
9
9;
练习1、计算下列各组数据的方差:
(1)6
6
6
6
6
6
6;
(2)5
5
6
6
6
7
7;
(3)3
3
4
6
8
9
9;
(4)3
3
3
6
9
9
9;
跟踪练习
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的
波动越小,越稳定
思考:
1,当数据比较分散时,方差值怎样?
2,当数据比较集中时,方差值怎样?
3、方差大小与数据的波动性大小有怎样的关系?
S2=
[
(x1-x)2+(x2-x)2+
+(xn-x)2
]
现在你能说说两名同学的成绩的波动的情况吗?
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定
S甲2甲的波动小些,数据更稳定
10
20
探究:为了选拔一名同学参加某市中学生射击竞赛,
某校对甲、乙两名同学的射击水平进行了测试,
两人在相同条件下各射靶10次.
①求方差S甲2;
求方差S乙2
②赛后,甲乙两个同学都说自己是胜者,争执不下.请你根据所学过的统计知识,进一步判断甲乙两个同学在这次测试中成绩谁优谁次,并说明理由。
=?
7
7
6
8
6
7
8
7
5
9
乙成绩
(环数)
=?
4
7
10
9
5
6
8
6
8
7
甲成绩
(环数)
X甲
X乙
例2.
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都
表演了舞剧《天鹅湖》,参加表演的女演员的身高
(单位:cm)分别是
甲团
163
164
164
165
165
165
166
167
乙团
163
164
164
165
166
167
167
168
哪个芭蕾舞团女演员的身高更整齐?
S甲2≈1.36
S乙2≈2.75
∵
S甲2<
S乙2
∴甲芭蕾舞团女演员的身高更整
齐
解:
练习
为了考察甲、乙两种小麦的长势,分别从中抽取
10株麦苗,测得苗高如下(单位:cm)
甲
12
13
14
15
10
17
12
11
15
11
乙
11
16
17
14
13
15
10
10
10
14
(1)分别计算两种小麦的平均苗高
(2)哪种小麦的长势比较整齐?
解:
方差越大,说明数据的波动越大,越不稳定.
1、样本方差的作用是(
)
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、
在样本方差的计算公式
数字10
表示
,数字20表示
.
2、样本5、6、7、8、9的方差是
.
跟踪练习二
D
2
样本平均数
样本容量
跟踪练习
练习2、
在方差的计算公式
则符号
依次表示为(
)
(A)方差,平均数,数据个数
(B)数据个数,方差,平均数
(C)平均数,数据个数,方差
(D)方差,数据个数,平均数
D
练习4、甲、乙两人各射击5次,命中环数如下:
甲:7,8,6,8,6
乙:9,5,6,7,8
其中射击技术稳定的是谁?
练习3、同班的两名学生在一年里各次的数学考试成绩的平均分相等,但他们的方差不相等,正确评价他们的数学学习情况是(
)
(A)学一样
(B)方差大的学生说明潜力大
(C)方差较小的学生成绩稳定
(D)方差较小的学生成绩不稳定
C
练习5、下表是NBA本赛季最近四场球,姚明、霍华德以及邓肯的得分对照(单位:分)
霍华德
18
20
11
31
姚明
21
22
25
12
邓肯
25
13
26
19
(1)通过以上数据,要从中选出两人进入最近最佳阵容,怎么办?
平均分:都是20分
霍华德得分的极差最大,因此姚明和邓肯的发挥较稳定,可以进入最佳阵容!
(2)如果要从两位最佳中选一个作为首发,你会选谁?为什么?
姚明得分的方差是23.5,而邓肯得分的方差是27.75。
因此姚明的发挥相对邓肯要稳定一些,所以姚明可以作为首发,而邓肯则作为替补。
小明的烦恼
?
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学
110;
②英语
10
建议:英语较稳定但要提高;
数学不够稳定有待努力进步!
小
结
1、什么是方差?
2、如何计算一组数据的方差?
3、方差对于我们解决实际问题有什么帮助?
练习:
1。样本方差的作用是(
)
(
A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
2.
在样本方差的计算公式
数字10
表示(
)数字20表示(
)
3.一个样本的方差是零,若中位数是a,则它的平均数是(
)
(A)等于
a
(B)不等于a
(C)大于a
(
D)小于a
4.
从种植密度相同的甲、乙两块玉米地里,各抽取一个容量足够大
的
样本,分别统计单株玉米的产量.结果:
=
下列
给出对两块玉米地的五种估计,哪几种是有道理的?
(1)甲块田平均产量较高
(2)甲块田单株产量比较稳定
(3)两块田平均产量大约相等
(4)两块田总产量大约相等
(5)乙块田总产量较高
<
D
样本容量
样本平均数
A
√
√
5.刘翔为了备战2008年奥运会,刻苦进行110米跨栏训练,为判断他的成绩是否稳定,教练对他10次训练的成绩进行统计分析,则教练需了解刘翔这10次成绩的(
)
A、众数
B、方差
C、平均数
D、频数
牛刀小试
B
作
业
教科书
第1题、第2题、第4题
谢谢各位老师莅临指导!
yuss
谢
谢
方差
复习回忆
1.什么是一组数据的极差?
极差反映了这组数据哪方面的特征?
答:
一组数据中的最大值减去最小值所得的差叫
做这组数据的极差,极差反映的是这组数据
的变化范围或变化幅度.
2、样本9.9,10.3,10.3,9.9,10.1的极差是
.
3、一组数据3、-1、0、2、x的极差是5,
且x为自然数,则x=
.
老师的烦恼
?
两个同学本学期五次测验的数学成绩分别如下:(单位:分)
假如要数学竞赛了,老师要从甲、乙两名同学中挑选一个参加。若你是老师,你认为挑选哪一位比较适宜?
甲
85
90
90
90
95
乙
95
85
95
85
90
创境引入
⑶
通过统计图,你认为挑
选哪一位比较适宜?为什么?
⑴
分别计算两名同学的平均成绩;
两名同学的测试成绩统计如下:
80
85
90
95
100
成绩(分)
0
1
2
3
4
5
考试次数
老师的烦恼
?
甲
85
90
90
90
95
乙
95
85
95
85
90
甲
乙
⑵
根据这两名同学的成绩在
下图中画出折线统计图;
谁的稳定性好?应以什么数据来衡量呢?
用各数据与平均值偏差的和来衡量数据的稳定性!
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
怎么办?
用偏差的平方和来衡量数据的稳定性!
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
50
100
老师的烦恼
?
若甲有六次测验成绩,而乙只有五次测验成绩,分别如下:
(单位:分)
甲
85
90
90
95
95
85
乙
95
85
95
85
90
甲同学成绩与平均成绩的偏差的平方和:
100
乙同学成绩与平均成绩的偏差的平方和:
100
两者又没有区别了,又该怎么办?
甲、乙的平均分:
想一想
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性
16.7
20
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2
、…
(xn-x)2
,那么我们用它们的平均数,即用
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2=
[(x1-x)2+
(x2-x)2
+…+
(xn-x)2
]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,
平方后,再平均”.
定义
1、样本方差的作用是(
)
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、
在样本方差的计算公式
数字10
表示
,数字20表示
.
2、样本5、6、7、8、9的方差是
.
练习
D
2
样本平均数
样本容量
4、计算下列各组数据的方差:
(1)6
6
6
6
6
6
6;
(2)5
5
6
6
6
7
7;
(3)3
3
4
6
8
9
9;
(2)3
3
3
6
9
9
9;
练习1、计算下列各组数据的方差:
(1)6
6
6
6
6
6
6;
(2)5
5
6
6
6
7
7;
(3)3
3
4
6
8
9
9;
(4)3
3
3
6
9
9
9;
跟踪练习
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的
波动越小,越稳定
思考:
1,当数据比较分散时,方差值怎样?
2,当数据比较集中时,方差值怎样?
3、方差大小与数据的波动性大小有怎样的关系?
S2=
[
(x1-x)2+(x2-x)2+
+(xn-x)2
]
现在你能说说两名同学的成绩的波动的情况吗?
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定
S甲2
10
20
探究:为了选拔一名同学参加某市中学生射击竞赛,
某校对甲、乙两名同学的射击水平进行了测试,
两人在相同条件下各射靶10次.
①求方差S甲2;
求方差S乙2
②赛后,甲乙两个同学都说自己是胜者,争执不下.请你根据所学过的统计知识,进一步判断甲乙两个同学在这次测试中成绩谁优谁次,并说明理由。
=?
7
7
6
8
6
7
8
7
5
9
乙成绩
(环数)
=?
4
7
10
9
5
6
8
6
8
7
甲成绩
(环数)
X甲
X乙
例2.
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都
表演了舞剧《天鹅湖》,参加表演的女演员的身高
(单位:cm)分别是
甲团
163
164
164
165
165
165
166
167
乙团
163
164
164
165
166
167
167
168
哪个芭蕾舞团女演员的身高更整齐?
S甲2≈1.36
S乙2≈2.75
∵
S甲2<
S乙2
∴甲芭蕾舞团女演员的身高更整
齐
解:
练习
为了考察甲、乙两种小麦的长势,分别从中抽取
10株麦苗,测得苗高如下(单位:cm)
甲
12
13
14
15
10
17
12
11
15
11
乙
11
16
17
14
13
15
10
10
10
14
(1)分别计算两种小麦的平均苗高
(2)哪种小麦的长势比较整齐?
解:
方差越大,说明数据的波动越大,越不稳定.
1、样本方差的作用是(
)
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、
在样本方差的计算公式
数字10
表示
,数字20表示
.
2、样本5、6、7、8、9的方差是
.
跟踪练习二
D
2
样本平均数
样本容量
跟踪练习
练习2、
在方差的计算公式
则符号
依次表示为(
)
(A)方差,平均数,数据个数
(B)数据个数,方差,平均数
(C)平均数,数据个数,方差
(D)方差,数据个数,平均数
D
练习4、甲、乙两人各射击5次,命中环数如下:
甲:7,8,6,8,6
乙:9,5,6,7,8
其中射击技术稳定的是谁?
练习3、同班的两名学生在一年里各次的数学考试成绩的平均分相等,但他们的方差不相等,正确评价他们的数学学习情况是(
)
(A)学一样
(B)方差大的学生说明潜力大
(C)方差较小的学生成绩稳定
(D)方差较小的学生成绩不稳定
C
练习5、下表是NBA本赛季最近四场球,姚明、霍华德以及邓肯的得分对照(单位:分)
霍华德
18
20
11
31
姚明
21
22
25
12
邓肯
25
13
26
19
(1)通过以上数据,要从中选出两人进入最近最佳阵容,怎么办?
平均分:都是20分
霍华德得分的极差最大,因此姚明和邓肯的发挥较稳定,可以进入最佳阵容!
(2)如果要从两位最佳中选一个作为首发,你会选谁?为什么?
姚明得分的方差是23.5,而邓肯得分的方差是27.75。
因此姚明的发挥相对邓肯要稳定一些,所以姚明可以作为首发,而邓肯则作为替补。
小明的烦恼
?
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学
110;
②英语
10
建议:英语较稳定但要提高;
数学不够稳定有待努力进步!
小
结
1、什么是方差?
2、如何计算一组数据的方差?
3、方差对于我们解决实际问题有什么帮助?
练习:
1。样本方差的作用是(
)
(
A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
2.
在样本方差的计算公式
数字10
表示(
)数字20表示(
)
3.一个样本的方差是零,若中位数是a,则它的平均数是(
)
(A)等于
a
(B)不等于a
(C)大于a
(
D)小于a
4.
从种植密度相同的甲、乙两块玉米地里,各抽取一个容量足够大
的
样本,分别统计单株玉米的产量.结果:
=
下列
给出对两块玉米地的五种估计,哪几种是有道理的?
(1)甲块田平均产量较高
(2)甲块田单株产量比较稳定
(3)两块田平均产量大约相等
(4)两块田总产量大约相等
(5)乙块田总产量较高
<
D
样本容量
样本平均数
A
√
√
5.刘翔为了备战2008年奥运会,刻苦进行110米跨栏训练,为判断他的成绩是否稳定,教练对他10次训练的成绩进行统计分析,则教练需了解刘翔这10次成绩的(
)
A、众数
B、方差
C、平均数
D、频数
牛刀小试
B
作
业
教科书
第1题、第2题、第4题
谢谢各位老师莅临指导!
yuss
谢
谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
