北师大版九年级上册数学1.3正方形的判定和性质课件(共38张PPT)
文档属性
| 名称 | 北师大版九年级上册数学1.3正方形的判定和性质课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-12 21:29:55 | ||
图片预览







文档简介
正方形的性质与判定
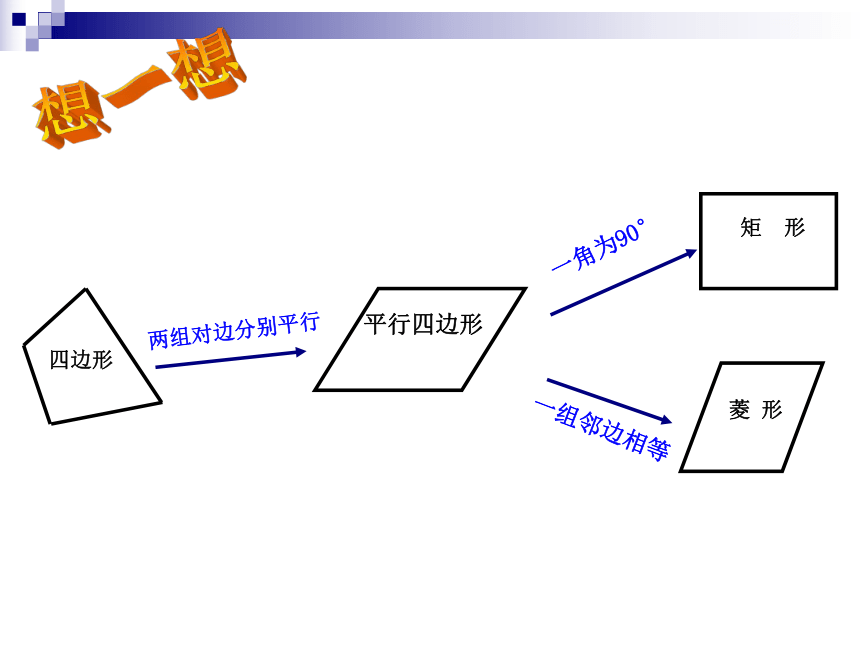
四边形
两组对边分别平行
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
你觉得什么样的四边形是正方形呢?
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探究(一)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
有一组邻边相等
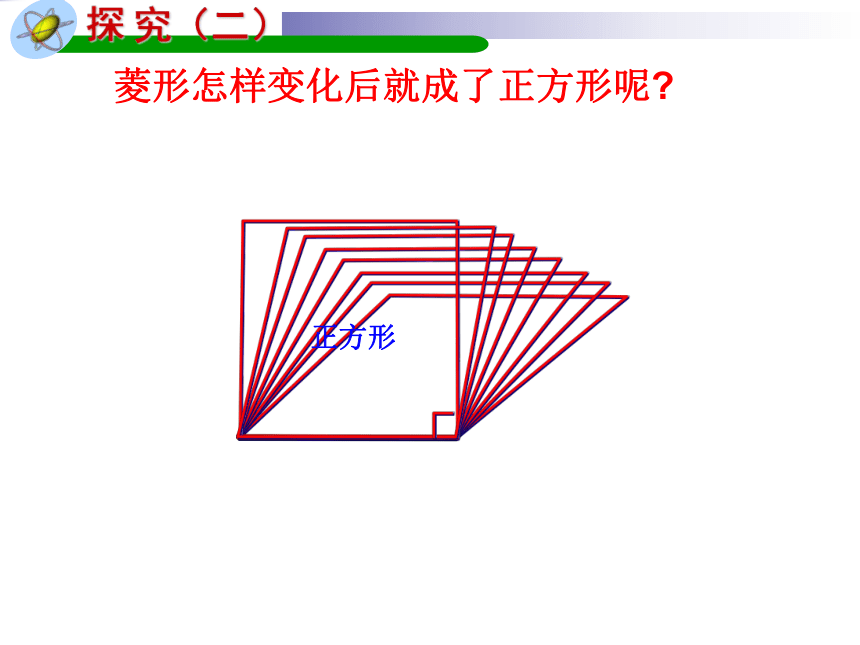
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
有一个角是直角
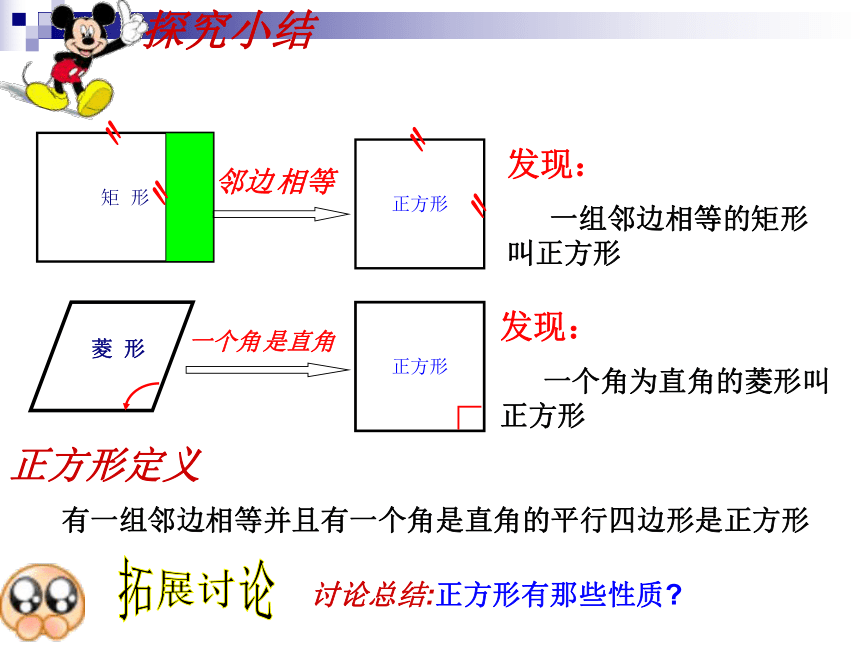
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
讨论总结:正方形有那些性质?
知识点一:
正方形的性质
观察思考:正方形是中心对称图形吗?
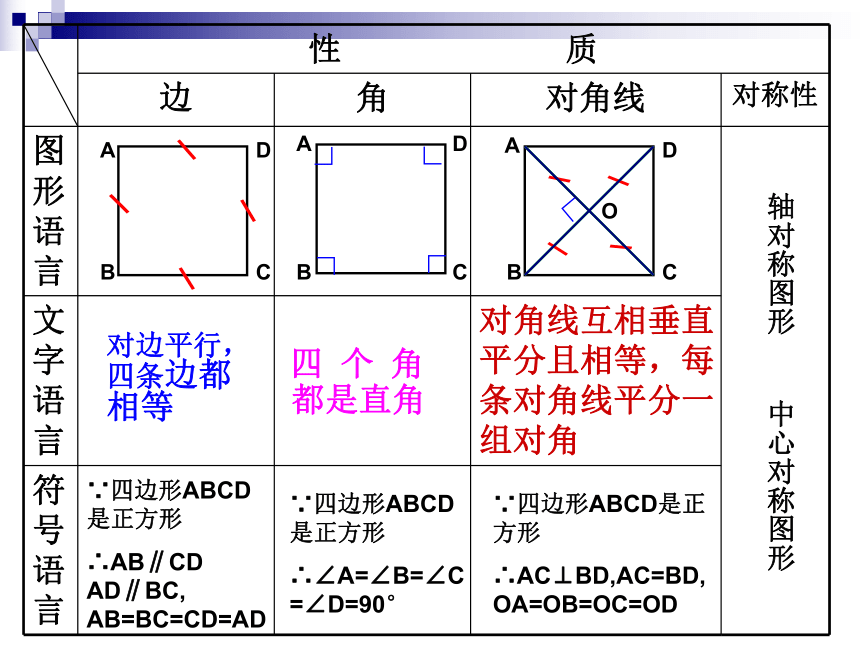
性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
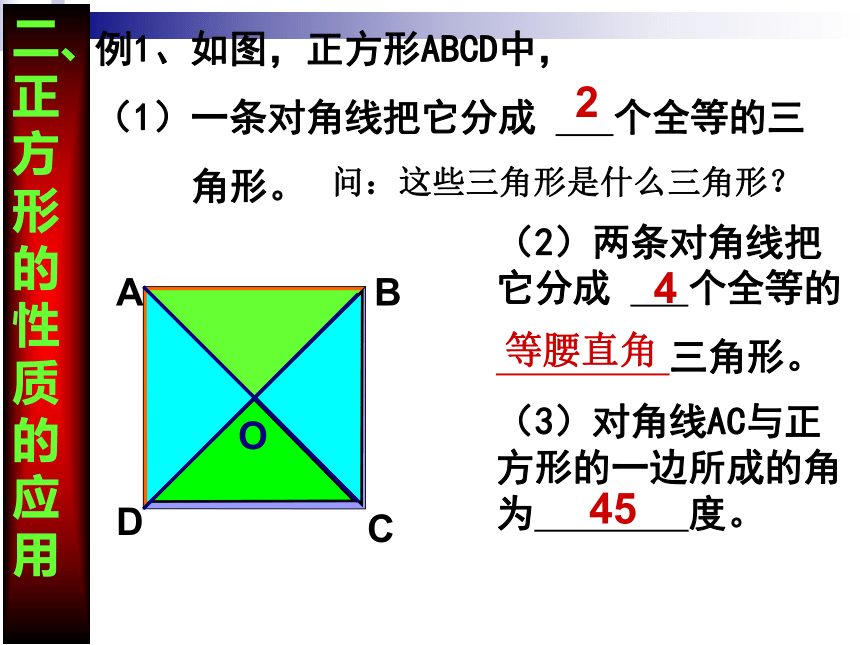
二、正方形的性质的应用
例1、如图,正方形ABCD中,
(1)一条对角线把它分成 个全等的三
角形。
问:这些三角形是什么三角形?
(2)两条对角线把它分成 个全等的
三角形。
2
4
等腰直角
A
B
D
C
O
(3)对角线AC与正方形的一边所成的角为 度。
45
例2、如图,正方形ABCD中,
A
B
D
C
O
正方形的面积为64平方厘米,则正方形对角线AC= 。
8√2 cm
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
C
2.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .
8cm
3.正方形的对角线和它的边所成的角是 度.
45°
4.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。
5.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一
点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= 。
5cm
A
B
C
D
F
P
E
O
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC⊥BD, 即∠AOB=∠BOC=∠COD=∠DOA=90°
AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO(SAS)
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
平行四边形
矩形
菱形
正
方
形
正方形、矩形、菱形、平行四边形四者之间有什么关系?
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
小结
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
知识拓展:与同学讨论后填写下表:
边
角
对 角 线
对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行,四边都相等
对边平行,
四条边
都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
知识点二:
正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
图形之间的变化关系
正方形的判定方法:
2、有一组邻边相等的矩形是正方形
3、有一个角是直角的菱形是正方形
1、一组邻边相等且有一个角是直角的平行四边形是正方形
(对角线相等且互相垂直平分的四边形是正方形)
判断四边形是正方形有哪些方法?
1、先说明它是矩形,再说明这个矩形有一组邻边相等.
2、先说明它是菱形,再说明这个菱形有一个角是直角.
3、先说明它是平行四边形,再说明有一组邻边相等,并且一个角是直角。
(对角线平分且垂直又相等的四边形是正方形)
(邻边相等的矩形是正方形)
(有一个角是直角的菱形是正方形)
巩固练习:判断下列命题是否正确,不是正方形的补充什么条件能让它成为正方形?
四个角都相等的四边形是正方形; ( )
四条边都相等的四边形是正方形; ( )
对角线相等的菱形是正方形; ( )
对角线互相垂直的矩形是正方形; ( )
对角线垂直且相等的四边形是正方形; ( )
四边相等,有一个角是直角的四边形
是正方形. ( )
√
√
√
×
×
×
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°;
AB=AD=DC=BC
(正方形的四条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌△CGF ≌△DHG.
∴ EH=EF=FG=GH
∴ 四边形EFGH是菱形
又∵ ∠3+∠2=90°且 ∠1=∠3
∴ ∠1+∠2=90°
∴ ∠EFG=90°
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
练习.如图,四边形ABCD是正方形,E、F、G、H分别是四边的中点。你知道四边形EFGH的形状吗?为什么?
A
B
C
D
E
F
G
H
2.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.
F
A
B
C
D
E
试说明:四边形DEBF是正方形.
解:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°,
又∵ ∠ABC=90°,
∴四边形DEBF是矩形
∵ BD平分∠ABC, DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
如图,在矩形ABCD中,四个角的平分线相交于点E、F、G、H,试说明四边形EFGH是正方形。
A
B
C
D
E
F
G
H
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角等于45°
边:
角:
对角线:
3、正方形有那些判定方法(请各同学根据自己的实际具体分类)
正方形的判定方法:
2、有一组邻边相等的矩形是正方形
3、有一个角是直角的菱形是正方形
1、一组邻边相等且有一个角是直角的平行四边形是正方形
(对角线相等且互相垂直平分的四边形是正方形)
正方形常考点练习巩固与提升
例:正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
25°
30°
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
如图,已知四边形ABCD和四边形DEFG是正方形,那么线段AE和DG有什么大小关系?请说明理由。
A
E
F
G
D
C
B
1
2
3
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、BE 、AC之间的大小关系,并证明你的猜想.
G
F
E
D
A
B
C
例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
AB=BC,∠1=∠2=45 °
AM=BN
△ABM≌△BCN
正方形ABCD
OM=ON
∠OMN=∠ONM=45°
活动与探索
A
B
C
D
E
F
如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450
G
变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。
四边形
两组对边分别平行
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
你觉得什么样的四边形是正方形呢?
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探究(一)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
有一组邻边相等
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
有一个角是直角
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
讨论总结:正方形有那些性质?
知识点一:
正方形的性质
观察思考:正方形是中心对称图形吗?
性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
二、正方形的性质的应用
例1、如图,正方形ABCD中,
(1)一条对角线把它分成 个全等的三
角形。
问:这些三角形是什么三角形?
(2)两条对角线把它分成 个全等的
三角形。
2
4
等腰直角
A
B
D
C
O
(3)对角线AC与正方形的一边所成的角为 度。
45
例2、如图,正方形ABCD中,
A
B
D
C
O
正方形的面积为64平方厘米,则正方形对角线AC= 。
8√2 cm
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
C
2.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .
8cm
3.正方形的对角线和它的边所成的角是 度.
45°
4.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。
5.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一
点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= 。
5cm
A
B
C
D
F
P
E
O
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC⊥BD, 即∠AOB=∠BOC=∠COD=∠DOA=90°
AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO(SAS)
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
平行四边形
矩形
菱形
正
方
形
正方形、矩形、菱形、平行四边形四者之间有什么关系?
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
小结
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
知识拓展:与同学讨论后填写下表:
边
角
对 角 线
对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行,四边都相等
对边平行,
四条边
都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
知识点二:
正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
图形之间的变化关系
正方形的判定方法:
2、有一组邻边相等的矩形是正方形
3、有一个角是直角的菱形是正方形
1、一组邻边相等且有一个角是直角的平行四边形是正方形
(对角线相等且互相垂直平分的四边形是正方形)
判断四边形是正方形有哪些方法?
1、先说明它是矩形,再说明这个矩形有一组邻边相等.
2、先说明它是菱形,再说明这个菱形有一个角是直角.
3、先说明它是平行四边形,再说明有一组邻边相等,并且一个角是直角。
(对角线平分且垂直又相等的四边形是正方形)
(邻边相等的矩形是正方形)
(有一个角是直角的菱形是正方形)
巩固练习:判断下列命题是否正确,不是正方形的补充什么条件能让它成为正方形?
四个角都相等的四边形是正方形; ( )
四条边都相等的四边形是正方形; ( )
对角线相等的菱形是正方形; ( )
对角线互相垂直的矩形是正方形; ( )
对角线垂直且相等的四边形是正方形; ( )
四边相等,有一个角是直角的四边形
是正方形. ( )
√
√
√
×
×
×
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°;
AB=AD=DC=BC
(正方形的四条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌△CGF ≌△DHG.
∴ EH=EF=FG=GH
∴ 四边形EFGH是菱形
又∵ ∠3+∠2=90°且 ∠1=∠3
∴ ∠1+∠2=90°
∴ ∠EFG=90°
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
练习.如图,四边形ABCD是正方形,E、F、G、H分别是四边的中点。你知道四边形EFGH的形状吗?为什么?
A
B
C
D
E
F
G
H
2.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.
F
A
B
C
D
E
试说明:四边形DEBF是正方形.
解:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°,
又∵ ∠ABC=90°,
∴四边形DEBF是矩形
∵ BD平分∠ABC, DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
如图,在矩形ABCD中,四个角的平分线相交于点E、F、G、H,试说明四边形EFGH是正方形。
A
B
C
D
E
F
G
H
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角等于45°
边:
角:
对角线:
3、正方形有那些判定方法(请各同学根据自己的实际具体分类)
正方形的判定方法:
2、有一组邻边相等的矩形是正方形
3、有一个角是直角的菱形是正方形
1、一组邻边相等且有一个角是直角的平行四边形是正方形
(对角线相等且互相垂直平分的四边形是正方形)
正方形常考点练习巩固与提升
例:正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
25°
30°
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
如图,已知四边形ABCD和四边形DEFG是正方形,那么线段AE和DG有什么大小关系?请说明理由。
A
E
F
G
D
C
B
1
2
3
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、BE 、AC之间的大小关系,并证明你的猜想.
G
F
E
D
A
B
C
例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
AB=BC,∠1=∠2=45 °
AM=BN
△ABM≌△BCN
正方形ABCD
OM=ON
∠OMN=∠ONM=45°
活动与探索
A
B
C
D
E
F
如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450
G
变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
