人教版九年级上册 数学 课件 21.2.1 配方法 (25张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 课件 21.2.1 配方法 (25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 991.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览




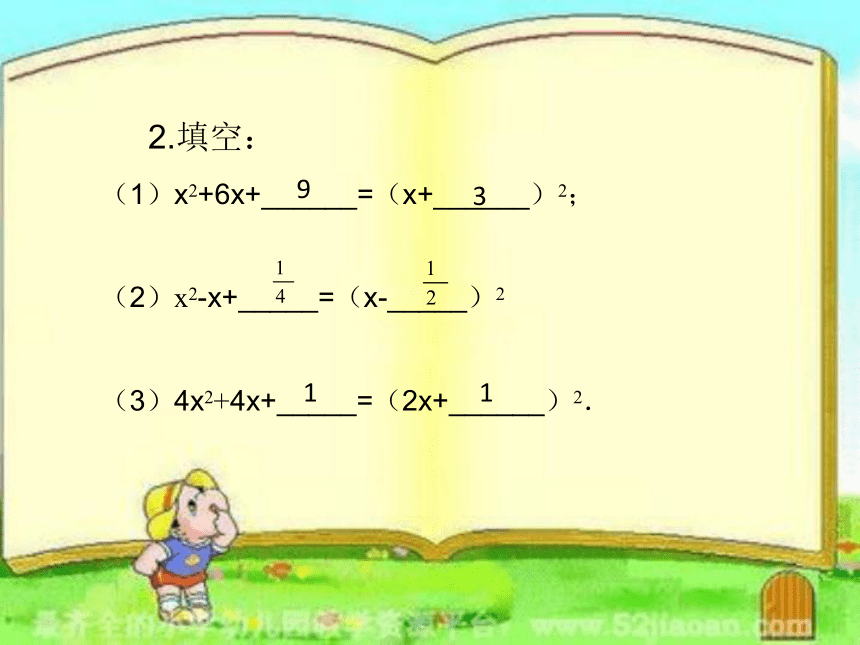



文档简介
21.2解一元二次方程(配方法)
知识回顾
因式分解的完全平方公式
3x2-1=5
4(x-1)2-9=0
1. 解下列方程
解:
3x2-1=5
4(x-1)2-9=0
移项,得
二次项系数化为1,得
降次
即
(1)x2+6x+______=(x+______)2;
(2)x2-x+_____=(x-_____)2
(3)4x2+4x+_____=(2x+______)2.
9
3
1
1
2.填空:
填一填
方程 可以化成 _________ ,
进行降次,得 ________ ,方程的根为
__ ____ , _______ .
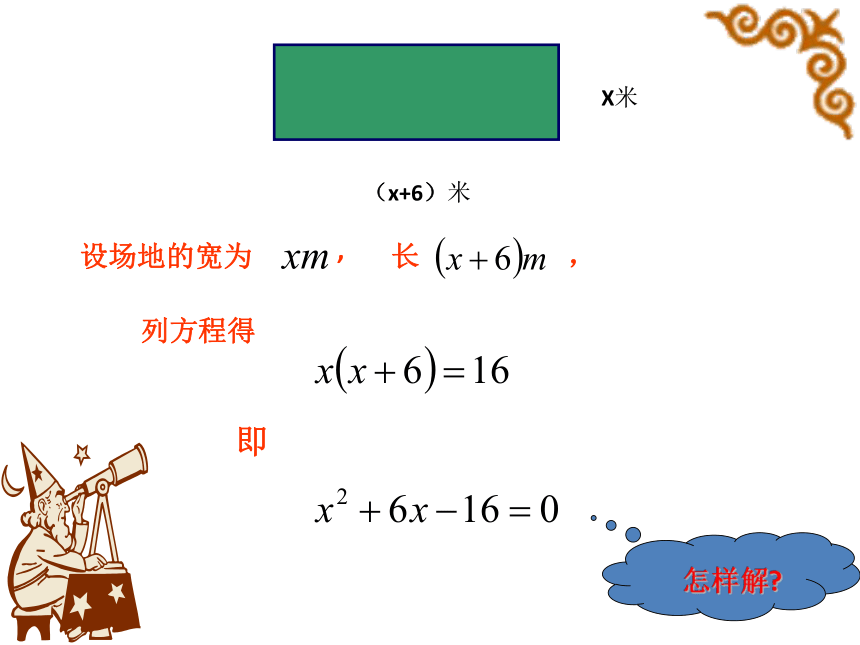
问题
要使一块长方形场地的长比宽多6m,并且
面积为16m2,场地的长和宽应各是多少?
(x+6)米
X米
即
列方程得
长
设场地的宽为
,
,
怎样解?
=
16
即
列方程得
宽
设场地的长为
,
,
X米
(x-6)米
怎样解?
想一想
方程 和方程
有何联系与区别呢?
一起来看一看
(不符合)
答:这个长方形的长为8 米 ,宽为2米.
一起来看一看
答:这个长方形的长为8 米 ,宽为2米.
(不符合)
1、以上解法中,为什么在方程x2+6x=16两边加9?加其他数行吗?
2、什么叫配方法?
3、配方法的目的是什么? 这也是配方法的基本
9是一次项系数6一半的平方,加9正好于x2+6x能够配成
一个完全平方式: x2 + 6x + 9= ( x + 3 )2
通过配成完全平方形式来解一元二次方程的方法.
配方是为了降次,
把一个一元二次方程转化成两个一元一次方程来解.
可以看出,
根据完全平方公式:
配方法:
怎样解方程 ?
?
探究
变形为
(X + m)2 =n
的形式.(n为非负常数)
移项
两边加上(3)2,使左边配成
左边写成完全平方形式
降次
的形式
2
2
2
b
bx
x
+
+
解:
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
例1用配方法解下列关于x的方程:
(1)x2-8x+1=0
(2)2x2+1=3x
(3)
解:
移项,得
配方,得
由此可得
移项,得
配方,得
二次项的系数化为1,得
由此可得
二次项系数不为1
又怎么办?
移项,得
二次项的系数化为1,得
配方,得
∴ 原方程无实数根.
方程的二次项系数不是1时,为便于配方,可以让方程的各项除以二次项系数.
课堂练习:
25
5
36
6
2.用配方法解下列关于x的方程
课后巩固
一、选择题
1.将二次三项式x2-4x+1配方后得( ).
A.(x-2)2+3 B.(x-2)2-3 C.(x+2)2+3 D.(x+2)2-3
2.已知x2-8x+15=0,左边化成含有x的完全平方式,
其中正确的是( ).
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
二、解方程:
(1)x2+10x+16=0
(2)
今天作业:
你还能进一步用配方法解一般的一元二次方程
ax2+bx+c=0 (a,b,c为常数且a不为0) 吗?
试试看。
这节课我们主要学习了用配方法来解一元二次方程,那么用配方法解一元二次方程的一般步骤是什么呢?
①移项。
②将二次项系数化为1。
③配方。
④两边开平方。
⑤求出方程的解。
(使用完全平方公式配方)
(降次化为一元一次方程)
注意:配方时, 方程两边同时加上的是一次项
项系数一半的平方.
谢谢大家!
知识回顾
因式分解的完全平方公式
3x2-1=5
4(x-1)2-9=0
1. 解下列方程
解:
3x2-1=5
4(x-1)2-9=0
移项,得
二次项系数化为1,得
降次
即
(1)x2+6x+______=(x+______)2;
(2)x2-x+_____=(x-_____)2
(3)4x2+4x+_____=(2x+______)2.
9
3
1
1
2.填空:
填一填
方程 可以化成 _________ ,
进行降次,得 ________ ,方程的根为
__ ____ , _______ .
问题
要使一块长方形场地的长比宽多6m,并且
面积为16m2,场地的长和宽应各是多少?
(x+6)米
X米
即
列方程得
长
设场地的宽为
,
,
怎样解?
=
16
即
列方程得
宽
设场地的长为
,
,
X米
(x-6)米
怎样解?
想一想
方程 和方程
有何联系与区别呢?
一起来看一看
(不符合)
答:这个长方形的长为8 米 ,宽为2米.
一起来看一看
答:这个长方形的长为8 米 ,宽为2米.
(不符合)
1、以上解法中,为什么在方程x2+6x=16两边加9?加其他数行吗?
2、什么叫配方法?
3、配方法的目的是什么? 这也是配方法的基本
9是一次项系数6一半的平方,加9正好于x2+6x能够配成
一个完全平方式: x2 + 6x + 9= ( x + 3 )2
通过配成完全平方形式来解一元二次方程的方法.
配方是为了降次,
把一个一元二次方程转化成两个一元一次方程来解.
可以看出,
根据完全平方公式:
配方法:
怎样解方程 ?
?
探究
变形为
(X + m)2 =n
的形式.(n为非负常数)
移项
两边加上(3)2,使左边配成
左边写成完全平方形式
降次
的形式
2
2
2
b
bx
x
+
+
解:
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
例1用配方法解下列关于x的方程:
(1)x2-8x+1=0
(2)2x2+1=3x
(3)
解:
移项,得
配方,得
由此可得
移项,得
配方,得
二次项的系数化为1,得
由此可得
二次项系数不为1
又怎么办?
移项,得
二次项的系数化为1,得
配方,得
∴ 原方程无实数根.
方程的二次项系数不是1时,为便于配方,可以让方程的各项除以二次项系数.
课堂练习:
25
5
36
6
2.用配方法解下列关于x的方程
课后巩固
一、选择题
1.将二次三项式x2-4x+1配方后得( ).
A.(x-2)2+3 B.(x-2)2-3 C.(x+2)2+3 D.(x+2)2-3
2.已知x2-8x+15=0,左边化成含有x的完全平方式,
其中正确的是( ).
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
二、解方程:
(1)x2+10x+16=0
(2)
今天作业:
你还能进一步用配方法解一般的一元二次方程
ax2+bx+c=0 (a,b,c为常数且a不为0) 吗?
试试看。
这节课我们主要学习了用配方法来解一元二次方程,那么用配方法解一元二次方程的一般步骤是什么呢?
①移项。
②将二次项系数化为1。
③配方。
④两边开平方。
⑤求出方程的解。
(使用完全平方公式配方)
(降次化为一元一次方程)
注意:配方时, 方程两边同时加上的是一次项
项系数一半的平方.
谢谢大家!
同课章节目录
