人教版九年级上册 数学 课件 22.2二次函数与一元二次方程(17张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 课件 22.2二次函数与一元二次方程(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 594.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
§22.2二次函数与一元二次方程
九年级上册
温故知新
思考:一次函数y=kx+b的图象与一元一次
方程kx+b=0的根有什么关系?
例1、一次函数y=x+2的图象与x轴的交点为( , )
例2 、一元一次方程 x+2=0的根为________
结论:一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
-2 0
X=-2
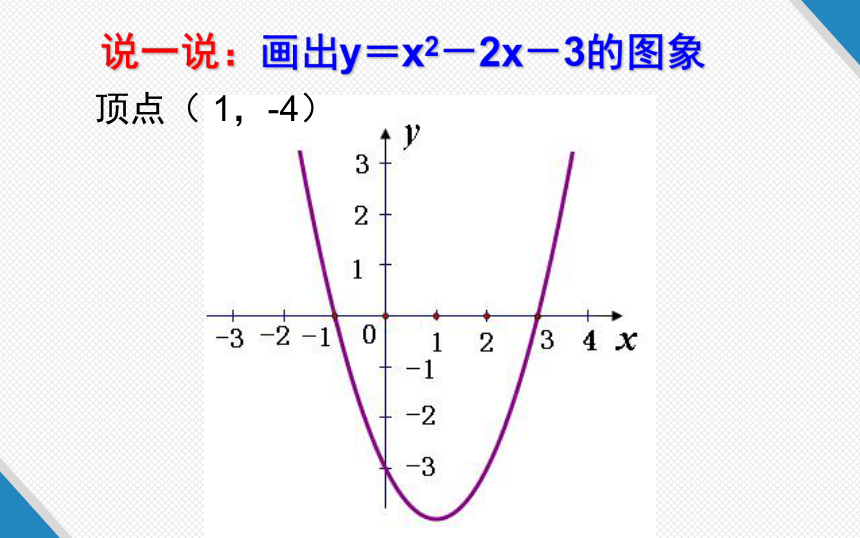
说一说:画出y=x2-2x-3的图象
顶点( 1,-4)
y=x2-2x-3
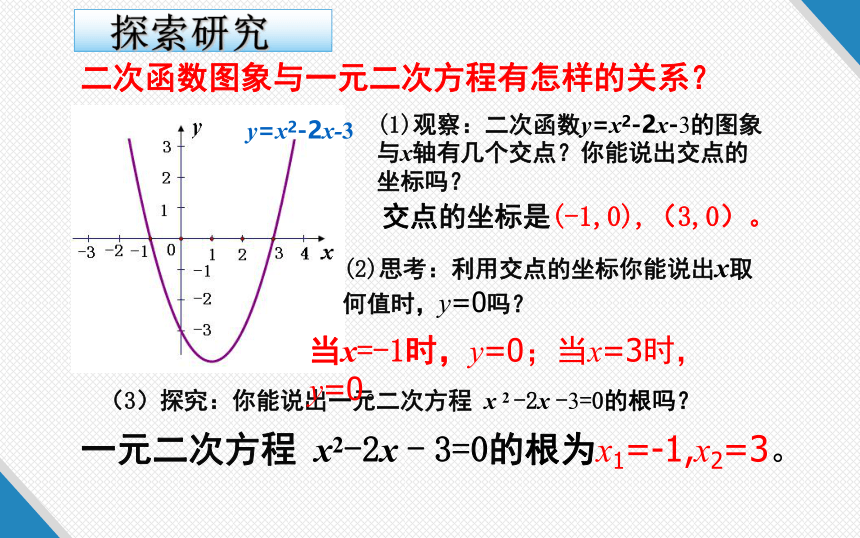
(1)观察:二次函数y=x2-2x-3的图象与x轴有几个交点?你能说出交点的坐标吗?
一元二次方程 x2-2x - 3=0的根为x1=-1,x2=3。
交点的坐标是(-1,0),(3,0)。
(3)探究:你能说出一元二次方程 x 2 -2x -3=0的根吗?
二次函数图象与一元二次方程有怎样的关系?
探索研究
当x=-1时,y=0;当x=3时,y=0。
(2)思考:利用交点的坐标你能说出x取何值时,y=0吗?
探究一:你发现了什么?
函数y=x2-2x-3的图象与x轴两个交点为
(-1,0)(3,0)
方程x2-2x-3 =0的两根是 x1= -1 , x2 = 3
结论一:
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根
(2)二次函数图象与x轴的交点问题可以转化为一元二次方程去解决
例题精讲
1. 求二次函数y=x2+4x-5图象与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解之得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0)(1,0)
结论一: (3)若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ) B( )
X1,0
X2,0
探究二:二次函数的图像与x轴的交点个数与一元二次方程的解有关系吗?
结论二:
函数与x轴有两个交点 方程有两不相等的根
函数与x轴有一个交点 方程有两相等的根
函数与x轴没有交点 方程没有根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论三:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数与x轴有两个交点
(2)b2-4ac=0 函数与x轴有一个交点
(3)b2-4ac<0 函数与x轴没有交点
例题精讲
2.不画图像,判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(1)∵ b2-4ac=02 -4×1×( -1 ) >0
∴此函数与x轴有两个交点
例题精讲
2.不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(2)∵ b2-4ac=
32 -4× (- 2)×( -9) < 0
∴函数与x轴没有交点
例题精讲
2.不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(3)
∵ b2-4ac=42 -4× 1×4 =0
∴函数与x轴有一个交点
例题精讲
2. 不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(4)
∵ b2-4ac=(a+b)2 -4× ( -a )×( -b) =( a - b)2 ≥0
∴函数与x轴有一个或两个交点
3 .一个小球从地面以一定的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ,其函数图象如下图所示.
请问小球经过多少秒后落地
解:方法一:利用函数图象解决问题。
图象与x轴的交点坐标为(0,0)(8,0),可知小球经过8秒后落地。
方法二:利用一元二次方程解决问题。 由h=0可得方程:
-5t 2+40t =0。解得:t1=0,t2=8,可知小球经过8秒后落地。
(1).用描点法作二次函数y=x2+2x-10的图象;
4、一元二次方程的图象解法
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0的根吗?
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.3和2.3(可将单位长再十等分,借助计算器确定其近似值,详见课本).
(3).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
交流总结
同学们,
通过这节课的学习,你收获了什么?
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
谢谢,再见!
§22.2二次函数与一元二次方程
九年级上册
温故知新
思考:一次函数y=kx+b的图象与一元一次
方程kx+b=0的根有什么关系?
例1、一次函数y=x+2的图象与x轴的交点为( , )
例2 、一元一次方程 x+2=0的根为________
结论:一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
-2 0
X=-2
说一说:画出y=x2-2x-3的图象
顶点( 1,-4)
y=x2-2x-3
(1)观察:二次函数y=x2-2x-3的图象与x轴有几个交点?你能说出交点的坐标吗?
一元二次方程 x2-2x - 3=0的根为x1=-1,x2=3。
交点的坐标是(-1,0),(3,0)。
(3)探究:你能说出一元二次方程 x 2 -2x -3=0的根吗?
二次函数图象与一元二次方程有怎样的关系?
探索研究
当x=-1时,y=0;当x=3时,y=0。
(2)思考:利用交点的坐标你能说出x取何值时,y=0吗?
探究一:你发现了什么?
函数y=x2-2x-3的图象与x轴两个交点为
(-1,0)(3,0)
方程x2-2x-3 =0的两根是 x1= -1 , x2 = 3
结论一:
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根
(2)二次函数图象与x轴的交点问题可以转化为一元二次方程去解决
例题精讲
1. 求二次函数y=x2+4x-5图象与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解之得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0)(1,0)
结论一: (3)若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ) B( )
X1,0
X2,0
探究二:二次函数的图像与x轴的交点个数与一元二次方程的解有关系吗?
结论二:
函数与x轴有两个交点 方程有两不相等的根
函数与x轴有一个交点 方程有两相等的根
函数与x轴没有交点 方程没有根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论三:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数与x轴有两个交点
(2)b2-4ac=0 函数与x轴有一个交点
(3)b2-4ac<0 函数与x轴没有交点
例题精讲
2.不画图像,判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(1)∵ b2-4ac=02 -4×1×( -1 ) >0
∴此函数与x轴有两个交点
例题精讲
2.不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(2)∵ b2-4ac=
32 -4× (- 2)×( -9) < 0
∴函数与x轴没有交点
例题精讲
2.不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(3)
∵ b2-4ac=42 -4× 1×4 =0
∴函数与x轴有一个交点
例题精讲
2. 不画图像,判断下列二次函数与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(4)
∵ b2-4ac=(a+b)2 -4× ( -a )×( -b) =( a - b)2 ≥0
∴函数与x轴有一个或两个交点
3 .一个小球从地面以一定的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ,其函数图象如下图所示.
请问小球经过多少秒后落地
解:方法一:利用函数图象解决问题。
图象与x轴的交点坐标为(0,0)(8,0),可知小球经过8秒后落地。
方法二:利用一元二次方程解决问题。 由h=0可得方程:
-5t 2+40t =0。解得:t1=0,t2=8,可知小球经过8秒后落地。
(1).用描点法作二次函数y=x2+2x-10的图象;
4、一元二次方程的图象解法
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0的根吗?
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.3和2.3(可将单位长再十等分,借助计算器确定其近似值,详见课本).
(3).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
交流总结
同学们,
通过这节课的学习,你收获了什么?
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
谢谢,再见!
同课章节目录
