人教版九年级上册 数学 课件: 22.1.4 二次函数y=ax2+bx+c的图象和性质(3)(25张)
文档属性
| 名称 | 人教版九年级上册 数学 课件: 22.1.4 二次函数y=ax2+bx+c的图象和性质(3)(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 19:38:51 | ||
图片预览

文档简介
二次函数的图象和性质(3)
—复习—
c=0
平移
y=ax2(a≠0)
y=ax2+c(a≠0)
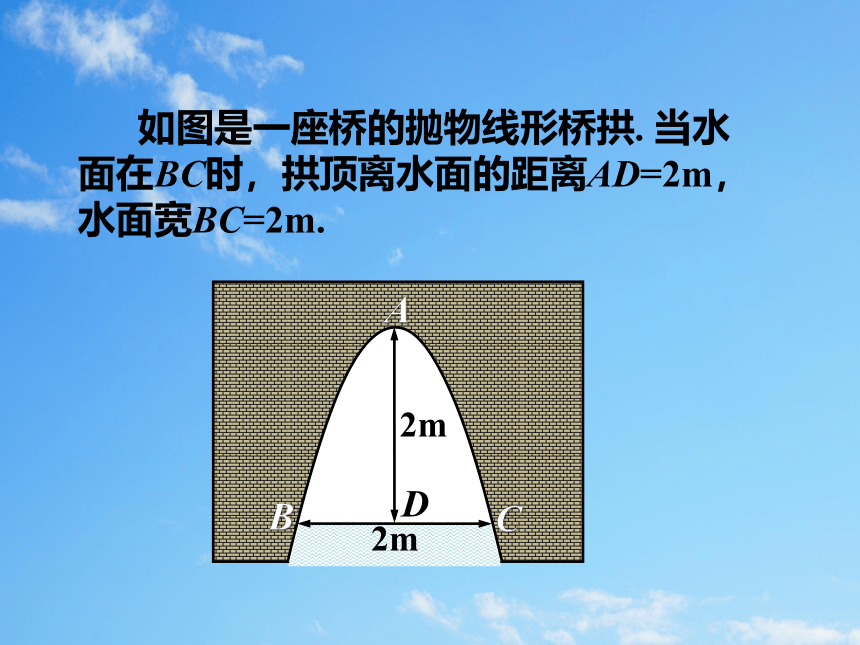
如图是一座桥的抛物线形桥拱. 当水面在BC时,拱顶离水面的距离AD=2m,水面宽BC=2m.
A
B
C
D
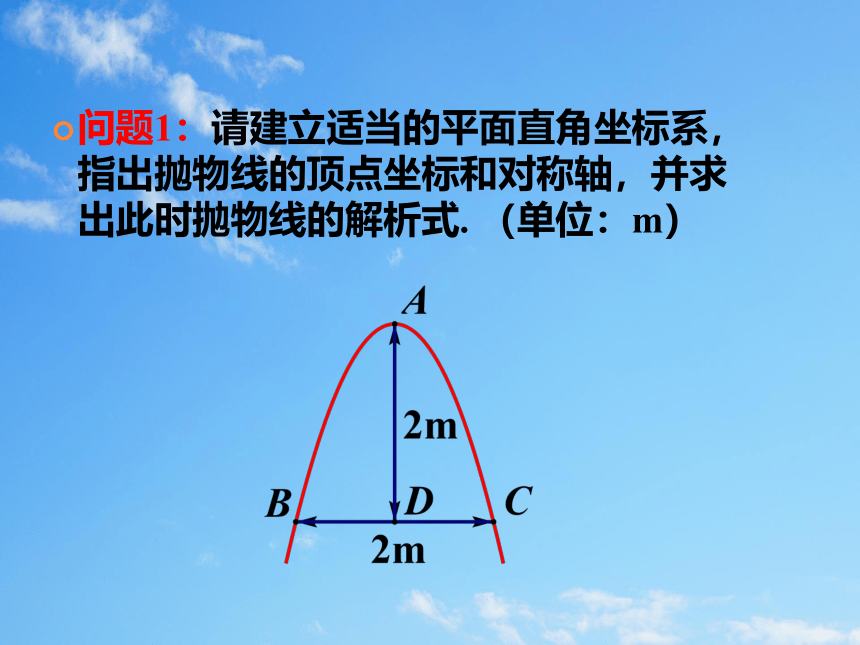
2m
2m
问题1:请建立适当的平面直角坐标系,指出抛物线的顶点坐标和对称轴,并求出此时抛物线的解析式. (单位:m)
x
y
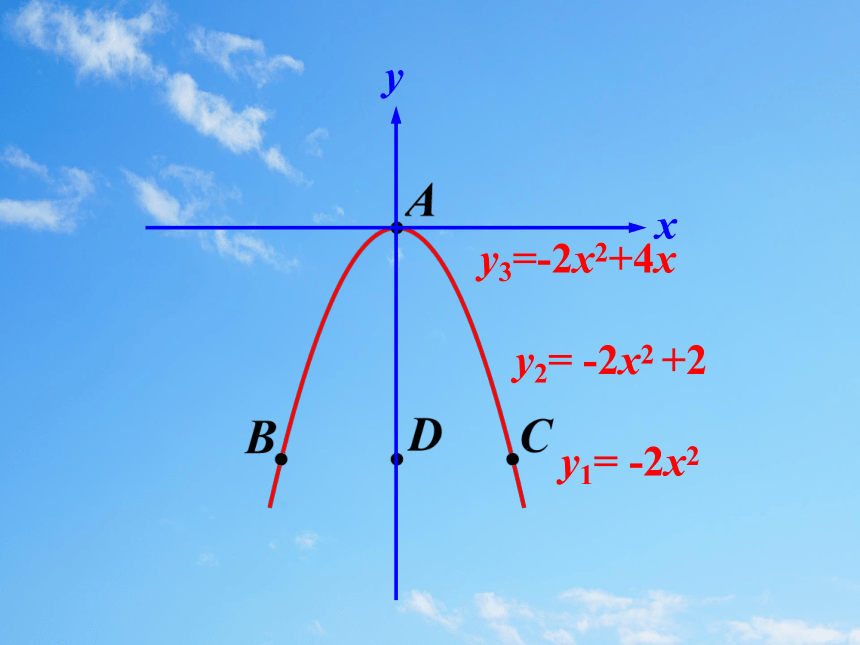
y1= -2x2
y2= -2x2 +2
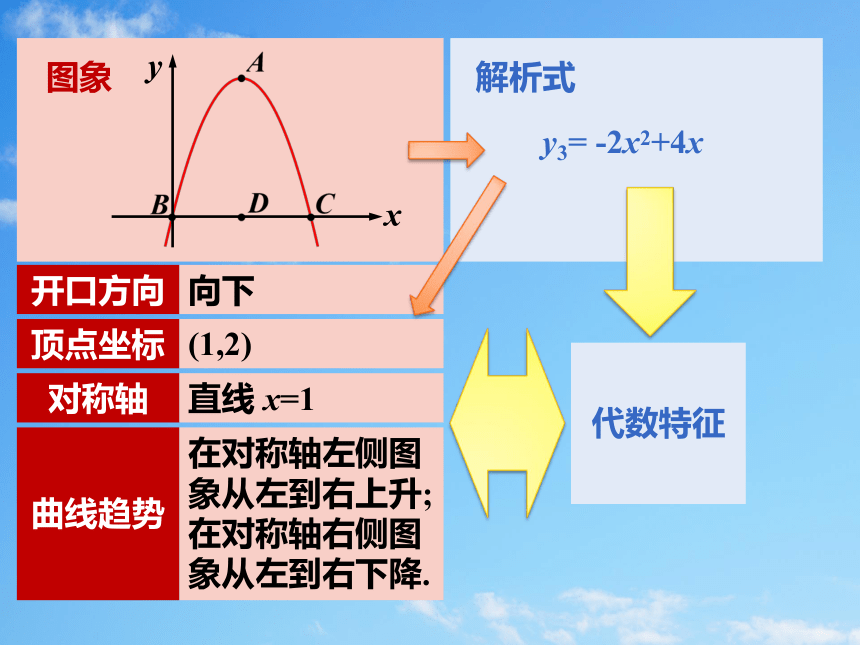
y3=-2x2+4x
解析式
图象
x
y
开口方向
顶点坐标
对称轴
曲线趋势
向下
(1,2)
直线 x=1
在对称轴左侧图象从左到右上升;
在对称轴右侧图象从左到右下降.
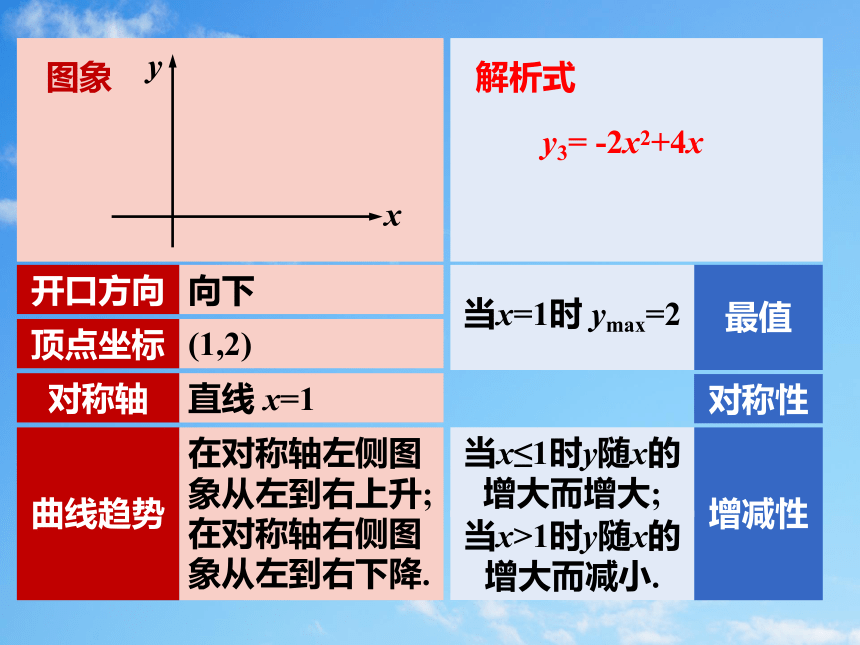
y3= -2x2+4x
代数特征
解析式
图象
x
y
开口方向
顶点坐标
对称轴
曲线趋势
向下
(1,2)
直线 x=1
在对称轴左侧图象从左到右上升;
在对称轴右侧图象从左到右下降.
最值
增减性
对称性
y3= -2x2+4x
当x=1时 ymax=2
当x>1时y随x的增大而减小.
当x≤1时y随x的增大而增大;
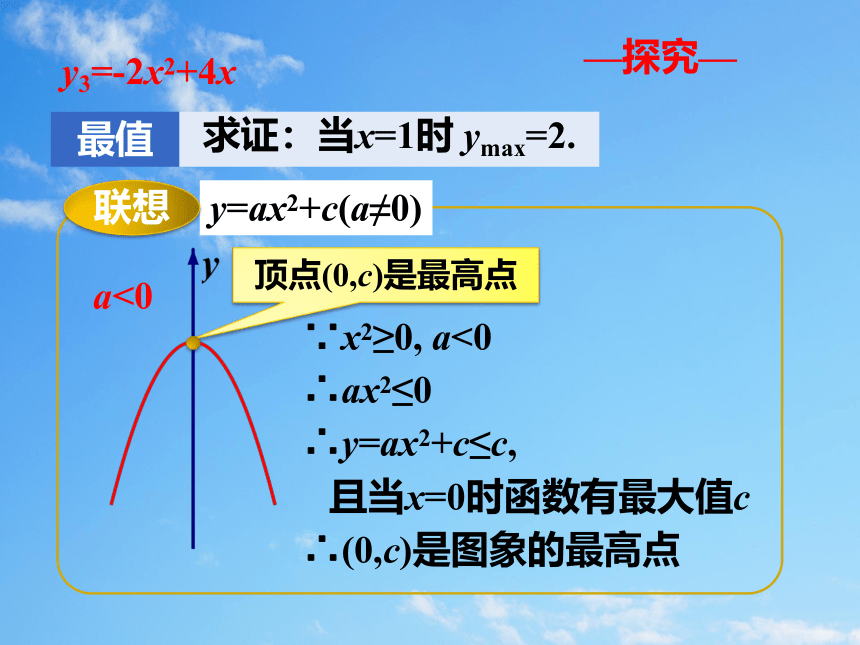
最值
求证:当x=1时 ymax=2.
—探究—
∵x2≥0, a<0
∴ax2≤0
∴y=ax2+c≤c,
且当x=0时函数有最大值c
∴(0,c)是图象的最高点
y=ax2+c(a≠0)
联想
a<0
顶点(0,c)是最高点
y3=-2x2+4x
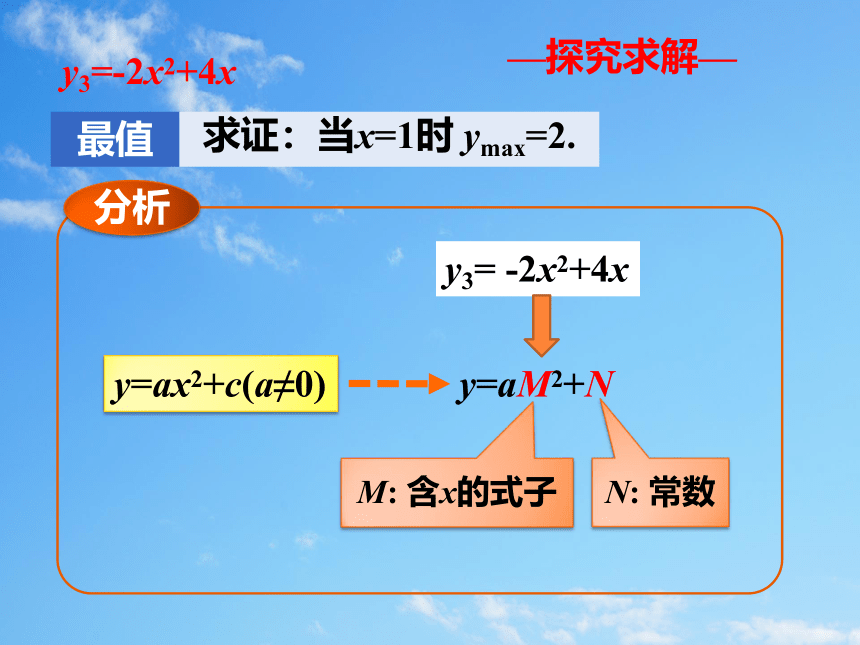
—探究求解—
y3= -2x2+4x
y=aM2+N
分析
M: 含x的式子
N: 常数
y=ax2+c(a≠0)
y3=-2x2+4x
最值
求证:当x=1时 ymax=2.
—探究求解—
y3 = -2x2+4x
= -2(x2-2x)
= -2(x2-2x+1)+2
= -2(x-1)2+2
∵(x-1)2≥0
∴ y3=-2(x-1)2+2≤2,且当x=1时,函数有最大值2.
( y3= -2x2+4x
y=aM2+N )
y3=-2x2+4x
最值
求证:当x=1时 ymax=2.
证明
—探究求解—
分析
y3 = - 2x2 + 4x = -2(x - 1)2 + 2
当x≤1时,x越大(x-1)2值越小,即y随x的增大而增大;
当x>1时,x越大(x-1)2值越大,即y随x的增大而减小.
y3=-2x2+4x
增减性
说明: 当x≤1时y随x的增大而增大;
当x>1时y随x的增大而减小.
x
y
m
m
yM=yN
xM
xN
x=1
对称性
说明:对任意m>0,
取xM=1-m 和 xN=1+m时,其对应的函数值相等.
—探究求解—
y3=-2x2+4x
M
N
x
y
y=n
x1
x2
x=1
对称性
—探究求解—
作直线y=n,则当n<2时直线与抛物线有两个公共点,说明:
y3=-2x2+4x
M
N
x
y
M(m,n)
N
x=1
对称性
设M(m,n)是抛物线上任意一点,说明:点M关于直线x=1的对称点N也在抛物线上.
—探究求解—
(2-m,n)
y3=-2x2+4x
小结
对称轴
顶点
坐标
最值
函 数 图 象
函 数 解 析 式
问题2:某同学算出桥拱的解析式是
y4= -2x2 + 4x - 2.
你知道他是怎么建立坐标系的吗?
—拓广迁移—
A
B
C
D
2m
2m
y4= -2x2+4x-2
问题2:y4= -2x2 + 4x - 2
解:配方
y4= -2x2+4x-2
= -2(x2-2x+1)
= -2(x-1)2
当x=1时函数有最大值0.
所以y4的顶点坐标为(1,0).
x
y
O
问题2:y4= -2x2 + 4x - 2
分析:
y4= -2x2+4x-2可看做由抛物线y3= -2x2+4x向下平移2个单位得到.
x
y
O
y3=-2x2+4x
y4=-2x2+4x-2
小试身手:试研究二次函数
的性质.
函数性质
图象特征
顶点坐标
对
称
轴
曲线趋势
向上
在对称轴左侧图象从左到右下降;
在对称轴右侧图象从左到右上升.
最值
增
减
性
对
称
性
当 时
开口方向
直线
对任意m>0,当自变量x分别取 和 时,对应的函数值相等.
当 时y随x的增大而减小;
当 时y随x的增大而增大.
—总结提升—
对于函数性质的研究,你有什么心得?
我们还能从哪些方面继续研究二次函数的性质呢?
数缺形时少直觉,
形缺数时难入微.
数形结合百般好,
隔离分家万事非.
——华罗庚
试研究下列二次函数的性质,
并作出图象:
课后作业
试用含a、b、c的式子表示二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标,并确定其开口方向.
课后作业
(选做)
问题3:在拱桥的问题中,
(1)你发现y1、y2、y3、y4
的图象之间有什么联系?
(2)如果以C为原点,直线BC为x轴,你能直接写出桥拱所在抛物线的解析式吗?和同学交流一下,看看谁的方法又快又好.
(3)在(2)的条件下,桥拱在水中的倒影y′也是抛物线,你能直接写出它的解析式吗?想一想,你的依据是什么.
课后作业
—复习—
c=0
平移
y=ax2(a≠0)
y=ax2+c(a≠0)
如图是一座桥的抛物线形桥拱. 当水面在BC时,拱顶离水面的距离AD=2m,水面宽BC=2m.
A
B
C
D
2m
2m
问题1:请建立适当的平面直角坐标系,指出抛物线的顶点坐标和对称轴,并求出此时抛物线的解析式. (单位:m)
x
y
y1= -2x2
y2= -2x2 +2
y3=-2x2+4x
解析式
图象
x
y
开口方向
顶点坐标
对称轴
曲线趋势
向下
(1,2)
直线 x=1
在对称轴左侧图象从左到右上升;
在对称轴右侧图象从左到右下降.
y3= -2x2+4x
代数特征
解析式
图象
x
y
开口方向
顶点坐标
对称轴
曲线趋势
向下
(1,2)
直线 x=1
在对称轴左侧图象从左到右上升;
在对称轴右侧图象从左到右下降.
最值
增减性
对称性
y3= -2x2+4x
当x=1时 ymax=2
当x>1时y随x的增大而减小.
当x≤1时y随x的增大而增大;
最值
求证:当x=1时 ymax=2.
—探究—
∵x2≥0, a<0
∴ax2≤0
∴y=ax2+c≤c,
且当x=0时函数有最大值c
∴(0,c)是图象的最高点
y=ax2+c(a≠0)
联想
a<0
顶点(0,c)是最高点
y3=-2x2+4x
—探究求解—
y3= -2x2+4x
y=aM2+N
分析
M: 含x的式子
N: 常数
y=ax2+c(a≠0)
y3=-2x2+4x
最值
求证:当x=1时 ymax=2.
—探究求解—
y3 = -2x2+4x
= -2(x2-2x)
= -2(x2-2x+1)+2
= -2(x-1)2+2
∵(x-1)2≥0
∴ y3=-2(x-1)2+2≤2,且当x=1时,函数有最大值2.
( y3= -2x2+4x
y=aM2+N )
y3=-2x2+4x
最值
求证:当x=1时 ymax=2.
证明
—探究求解—
分析
y3 = - 2x2 + 4x = -2(x - 1)2 + 2
当x≤1时,x越大(x-1)2值越小,即y随x的增大而增大;
当x>1时,x越大(x-1)2值越大,即y随x的增大而减小.
y3=-2x2+4x
增减性
说明: 当x≤1时y随x的增大而增大;
当x>1时y随x的增大而减小.
x
y
m
m
yM=yN
xM
xN
x=1
对称性
说明:对任意m>0,
取xM=1-m 和 xN=1+m时,其对应的函数值相等.
—探究求解—
y3=-2x2+4x
M
N
x
y
y=n
x1
x2
x=1
对称性
—探究求解—
作直线y=n,则当n<2时直线与抛物线有两个公共点,说明:
y3=-2x2+4x
M
N
x
y
M(m,n)
N
x=1
对称性
设M(m,n)是抛物线上任意一点,说明:点M关于直线x=1的对称点N也在抛物线上.
—探究求解—
(2-m,n)
y3=-2x2+4x
小结
对称轴
顶点
坐标
最值
函 数 图 象
函 数 解 析 式
问题2:某同学算出桥拱的解析式是
y4= -2x2 + 4x - 2.
你知道他是怎么建立坐标系的吗?
—拓广迁移—
A
B
C
D
2m
2m
y4= -2x2+4x-2
问题2:y4= -2x2 + 4x - 2
解:配方
y4= -2x2+4x-2
= -2(x2-2x+1)
= -2(x-1)2
当x=1时函数有最大值0.
所以y4的顶点坐标为(1,0).
x
y
O
问题2:y4= -2x2 + 4x - 2
分析:
y4= -2x2+4x-2可看做由抛物线y3= -2x2+4x向下平移2个单位得到.
x
y
O
y3=-2x2+4x
y4=-2x2+4x-2
小试身手:试研究二次函数
的性质.
函数性质
图象特征
顶点坐标
对
称
轴
曲线趋势
向上
在对称轴左侧图象从左到右下降;
在对称轴右侧图象从左到右上升.
最值
增
减
性
对
称
性
当 时
开口方向
直线
对任意m>0,当自变量x分别取 和 时,对应的函数值相等.
当 时y随x的增大而减小;
当 时y随x的增大而增大.
—总结提升—
对于函数性质的研究,你有什么心得?
我们还能从哪些方面继续研究二次函数的性质呢?
数缺形时少直觉,
形缺数时难入微.
数形结合百般好,
隔离分家万事非.
——华罗庚
试研究下列二次函数的性质,
并作出图象:
课后作业
试用含a、b、c的式子表示二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标,并确定其开口方向.
课后作业
(选做)
问题3:在拱桥的问题中,
(1)你发现y1、y2、y3、y4
的图象之间有什么联系?
(2)如果以C为原点,直线BC为x轴,你能直接写出桥拱所在抛物线的解析式吗?和同学交流一下,看看谁的方法又快又好.
(3)在(2)的条件下,桥拱在水中的倒影y′也是抛物线,你能直接写出它的解析式吗?想一想,你的依据是什么.
课后作业
同课章节目录
