人教版九年级上册 数学24.4 弧长和扇形面积课件(19张ppt)
文档属性
| 名称 | 人教版九年级上册 数学24.4 弧长和扇形面积课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 863.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 09:45:17 | ||
图片预览



文档简介
24.4.1 弧长和扇形面积
o
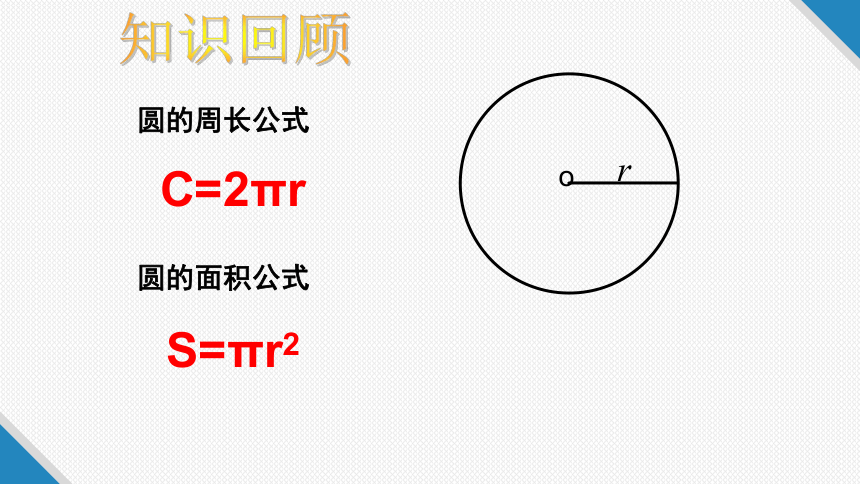
圆的周长公式
圆的面积公式
C=2πr
S=πr2
知识回顾
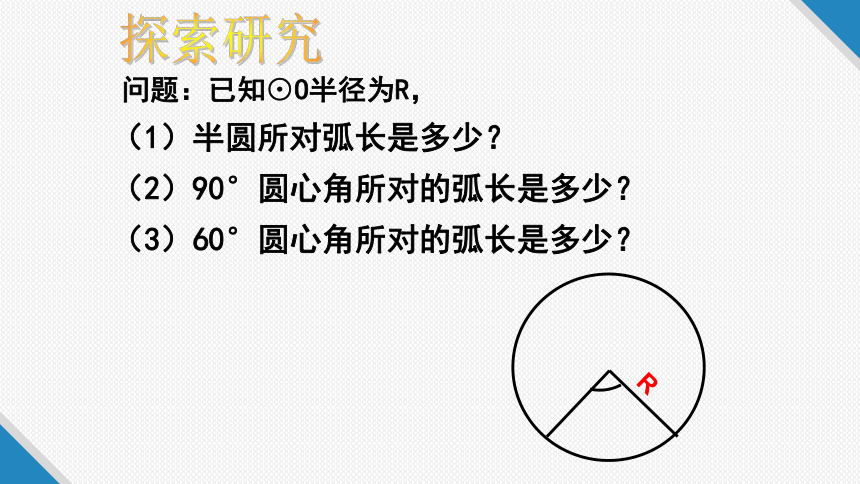
(1)半圆所对弧长是多少?
(2)90°圆心角所对的弧长是多少?
(3)60°圆心角所对的弧长是多少?
R
探索研究
问题:已知⊙O半径为R,
圆的周长可以看作___度的圆心角所对的弧.
1°的圆心角所对的弧长是 .
2°的圆心角所对的弧长是 .
n°圆心角所对的弧长是多少?
360
3°的圆心角所对的弧长是
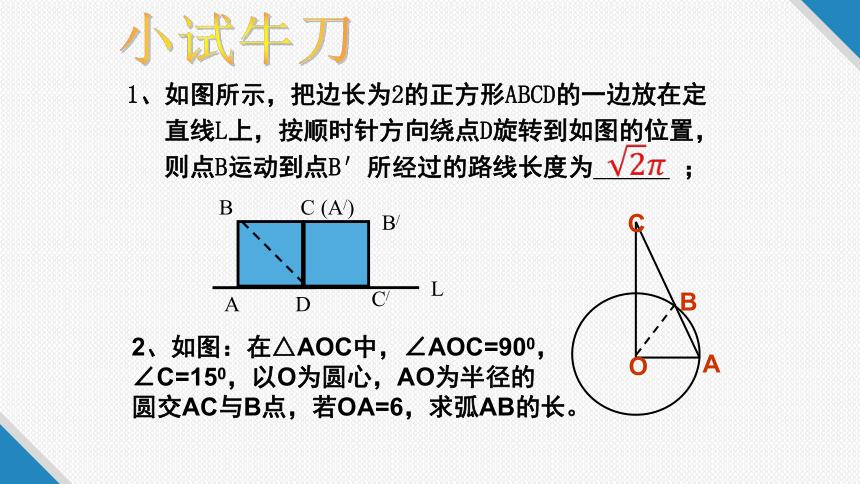
1、如图所示,把边长为2的正方形ABCD的一边放在定
直线L上,按顺时针方向绕点D旋转到如图的位置,
则点B运动到点B′所经过的路线长度为______ ;
A
C
B
D
B/
C/
(A/)
L
小试牛刀
2、如图:在△AOC中,∠AOC=900,
∠C=150,以O为圆心,AO为半径的
圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
?
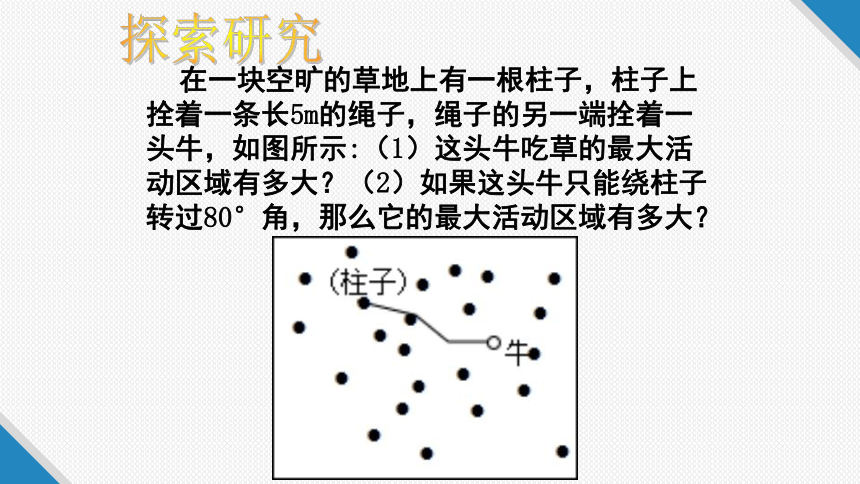
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
探索研究
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
(1)半圆的面积是多少?
(2)圆心角为90°的扇形面积是多少?
(3)圆心角为60°的扇形面积是多少?
探索研究
问题:已知⊙O半径为R,
1°的圆心角所对的扇形面积 =_______.
2°的圆心角所对的扇形面积 =_______.
3°的圆心角所对的扇形面积 =_______.
圆心角是 n°的扇形面积是多少?
S扇形=
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、已知半径为2的扇形,弧长为 ,
则它的面积为 .
4π
小试牛刀
2、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两
不相交,且半径都是2cm,求图中
阴影部分的面积。
例:如图、水平放置的圆柱形排水管道的截面
半径是0.6m,其中水面高0.3m,求截面
上有水部分的面积。
0
B
A
C
D
例题讲解
弓形的面积 = S扇-S△
变式:如图、水平放置的圆柱形排水管道
的截面半径是0.6cm,其中水面高
0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
变式:如图,A是半径为1的圆O外一点,且OA=2,
AB是⊙O的切线,BC//OA,连结AC,则阴
影部分面积等于 。
一、弧长的计算公式
二、扇形面积计算公式
课堂小结
这节课你有什么收获?
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕 点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的面积是
一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
●
B
B1
B2
A
D
B
C
.E
如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
生活中的数学
思考题
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
知识回顾
(1)半圆所对弧长是多少?
(2)90°圆心角所对的弧长是多少?
(3)60°圆心角所对的弧长是多少?
R
探索研究
问题:已知⊙O半径为R,
圆的周长可以看作___度的圆心角所对的弧.
1°的圆心角所对的弧长是 .
2°的圆心角所对的弧长是 .
n°圆心角所对的弧长是多少?
360
3°的圆心角所对的弧长是
1、如图所示,把边长为2的正方形ABCD的一边放在定
直线L上,按顺时针方向绕点D旋转到如图的位置,
则点B运动到点B′所经过的路线长度为______ ;
A
C
B
D
B/
C/
(A/)
L
小试牛刀
2、如图:在△AOC中,∠AOC=900,
∠C=150,以O为圆心,AO为半径的
圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
?
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
探索研究
什 么 是 扇 形 ?
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
(1)半圆的面积是多少?
(2)圆心角为90°的扇形面积是多少?
(3)圆心角为60°的扇形面积是多少?
探索研究
问题:已知⊙O半径为R,
1°的圆心角所对的扇形面积 =_______.
2°的圆心角所对的扇形面积 =_______.
3°的圆心角所对的扇形面积 =_______.
圆心角是 n°的扇形面积是多少?
S扇形=
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、已知半径为2的扇形,弧长为 ,
则它的面积为 .
4π
小试牛刀
2、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两
不相交,且半径都是2cm,求图中
阴影部分的面积。
例:如图、水平放置的圆柱形排水管道的截面
半径是0.6m,其中水面高0.3m,求截面
上有水部分的面积。
0
B
A
C
D
例题讲解
弓形的面积 = S扇-S△
变式:如图、水平放置的圆柱形排水管道
的截面半径是0.6cm,其中水面高
0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
变式:如图,A是半径为1的圆O外一点,且OA=2,
AB是⊙O的切线,BC//OA,连结AC,则阴
影部分面积等于 。
一、弧长的计算公式
二、扇形面积计算公式
课堂小结
这节课你有什么收获?
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕 点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的面积是
一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
●
B
B1
B2
A
D
B
C
.E
如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
生活中的数学
思考题
同课章节目录
