人教版八年级上册数学 11.1.1 三角形的边同步课件(25张)
文档属性
| 名称 | 人教版八年级上册数学 11.1.1 三角形的边同步课件(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 10:50:09 | ||
图片预览







文档简介
三角形
?
第十一章
11.1.1 三角形的边
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解三角形中的相关概念,学会用符号语言表示三角形中的对应元素.理解并且灵活应用三角形三边关系.
课前学案
1.由不在______________的三条线段首尾顺次相接所组
成的图形叫做三角形.
2.以A,B,C为顶点的三角形记作_______,读作
“______________”.
3.三角形按边分类,可分为________________和
________________.
4.三角形两边的和__________第三边,两边的差
__________第三边.
同一条直线
三角形ABC
等腰三角形
不等边三角形
大于
小于
△ABC
【例1】如右下图所示,图中共有三角形( )
A. 6个
B. 7个
C. 8个
D. 9个
C
课前导案
【解析】根据三角形的定义,让不在同一条直线上的三个点组合即可.找的时候要有顺序.共有△ABC,△ABE,△ACD,△BCF,△BCD,△BCE, △BFD,△CFE 8个三角形.
【点拔】注意找的时候要有顺序,也可从小到大找.
课前导案
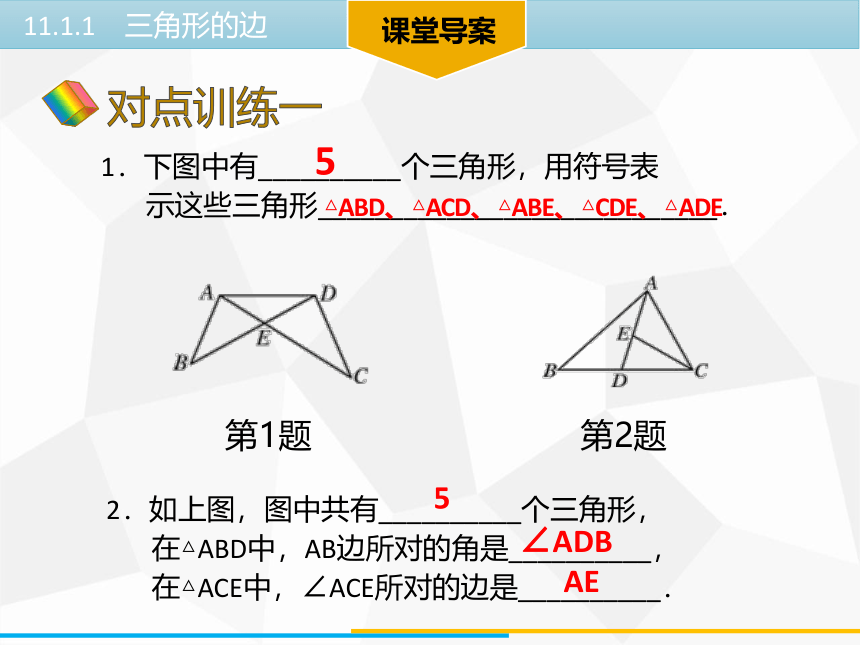
2.如上图,图中共有__________个三角形,
在△ABD中,AB边所对的角是__________,
在△ACE中,∠ACE所对的边是__________.
1.下图中有__________个三角形,用符号表
示这些三角形____________________________.
课堂导案
5
△ABD、△ACD、△ABE、△CDE、△ADE
5
∠ADB
AE
第2题
第1题
课堂导案
【例2】三角形按边可分为( )
A. 等腰三角形,直角三角形,锐角三角形
B. 直角三角形,不等边三角形
C. 等腰三角形,不等边三角形
D. 等腰三角形,等边三角形
【解析】三角形按边分类即有三条边都不相等和有两
条边相等,所以分为了不等边三角形和等腰
三角形.等边三角形是特殊的等腰三角形.
C
课堂导案
【点拔】掌握三角形的两种分类方法.按边分为:不等边三角形和等腰三角形;按角分为:锐角三角形、直角三角形、钝角三角形.
3.三角形按边的相等关系分类如下:
三角形
( )内可填入的是________________.
课堂导案
等边三角形
4.下列说法正确的是( )
A. 等腰三角形是等边三角形
B. 等边三角形是等腰三角形
C. 等腰三角形一定是锐角三角形
D. 等腰三角形一定是钝角三角形
课堂导案
B
课堂导案
【例3】已知三角形的两边为3和4,则第三边a的取值范围是__________.
【解析】根据三角形的三边关系,得4-3<a<4+3,即1<a<7.
【答案】1<a<7.
【点拔】已知两边的值,则第三边的范围是:大于两边的差,而小于两边的和.
1<a<7
课堂导案
5. 下列长度的各组线段,可以组成三角形的
是( )
A. 1,2,3 B. 3,3,6
C. 2,4,6 D. 4,5,8
6.三角形的三边长分别为5,8,x,则第三
边长x的取值范围是( )
A.3<x<8 B. 5<x<13
C.3<x<13 D. 8<x<13
D
C
7.一个等腰三角形的两边长分别为2和5,
则它的周长为( )
A. 7 B. 9
C. 12 D.9或12
课堂导案
C
课后练案
8.一个三角形的两边长分别是5cm和2cm,则它的第三边不可能是( )
A. 6cm B. 5cm C. 4cm D. 2cm
9.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种 B.2种 C.3种 D.4种
D
C
课后练案
10.已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A. 10 B.13
C. 17 D.13或17
C
11.如下图,图中有______个三角形,把它们用符号分别表示为_______________________________________,在△BCD中,CD边所对的角是__________.
课后练案
第11题
第12题
12.如上图,以∠C为一个内角的三角形是_________ ______,△AED的三个内角是________________________.
5
△ABC、△EBC、△ABD、△CDE、△BCD
∠DBC
△ABC、 △ ACD、
△ACE
∠ADE、∠AED、∠DAE
课后练案
13.若△ABC的三条边长分别为6,7,x,则x的取值范围是_____________.
14.一个三角形两边长分别为3和8,第三边长为奇数,则第三边长为__________.
1<x<3
7或9
15.已知等腰三角形的周长是16cm.
(1)若其中一边长为6cm,求另外两边长;
(2)若其中一边长为4cm,求另外两边长.
课后练案
6cm、4cm或5cm、5cm
6cm、6cm
16.已知,三角形三边的比是3∶4∶5,且最大边长与最小边长的差是4,求这个三角形的三条边的长.
课后练案
解:设三角形的三边分别为3x、4x、5x,根据题意有:5x-3x=4,解得x=2,3x=6,4x=8,5x=10.答:三角形三边长分别为6;8;10.
17.已知,在△ABC中,AB=8,且BC=2a+2,AC=22,
(1)求a的取值范围;
课后练案
由题意,得22-8<2a+2<22+8,解得6<a<14.
课后练案
(2)若△ABC为等腰三角形,求这个三角形的周长.
△ABC为等腰三角形,则2a+2=8或2a+2=22,解得a=3或a=10,
∵6<a<14,∴a=10,
∴△ABC的周长为22+22+8=52.
能力培优
18.已知:a、b、c是△ABC的三边,且a=4,b=6,若三角形的周长是小于18的偶数.
(1)求c边的长;
由条件得6-4<c<6+4,∴2<c<10,∴12<△ABC的周长<22,又因为△ABC的周长是小于18的偶数,∴△ABC的周长为14或16,当△ABC的周长为14时,c=4,当△ABC的周长为16时,c=6.
能力培优
(2)判断△ABC的形状.
当c=4时,a=c;当c=6时,b=c,所以△ABC是等腰三角形.
感谢聆听
?
第十一章
11.1.1 三角形的边
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解三角形中的相关概念,学会用符号语言表示三角形中的对应元素.理解并且灵活应用三角形三边关系.
课前学案
1.由不在______________的三条线段首尾顺次相接所组
成的图形叫做三角形.
2.以A,B,C为顶点的三角形记作_______,读作
“______________”.
3.三角形按边分类,可分为________________和
________________.
4.三角形两边的和__________第三边,两边的差
__________第三边.
同一条直线
三角形ABC
等腰三角形
不等边三角形
大于
小于
△ABC
【例1】如右下图所示,图中共有三角形( )
A. 6个
B. 7个
C. 8个
D. 9个
C
课前导案
【解析】根据三角形的定义,让不在同一条直线上的三个点组合即可.找的时候要有顺序.共有△ABC,△ABE,△ACD,△BCF,△BCD,△BCE, △BFD,△CFE 8个三角形.
【点拔】注意找的时候要有顺序,也可从小到大找.
课前导案
2.如上图,图中共有__________个三角形,
在△ABD中,AB边所对的角是__________,
在△ACE中,∠ACE所对的边是__________.
1.下图中有__________个三角形,用符号表
示这些三角形____________________________.
课堂导案
5
△ABD、△ACD、△ABE、△CDE、△ADE
5
∠ADB
AE
第2题
第1题
课堂导案
【例2】三角形按边可分为( )
A. 等腰三角形,直角三角形,锐角三角形
B. 直角三角形,不等边三角形
C. 等腰三角形,不等边三角形
D. 等腰三角形,等边三角形
【解析】三角形按边分类即有三条边都不相等和有两
条边相等,所以分为了不等边三角形和等腰
三角形.等边三角形是特殊的等腰三角形.
C
课堂导案
【点拔】掌握三角形的两种分类方法.按边分为:不等边三角形和等腰三角形;按角分为:锐角三角形、直角三角形、钝角三角形.
3.三角形按边的相等关系分类如下:
三角形
( )内可填入的是________________.
课堂导案
等边三角形
4.下列说法正确的是( )
A. 等腰三角形是等边三角形
B. 等边三角形是等腰三角形
C. 等腰三角形一定是锐角三角形
D. 等腰三角形一定是钝角三角形
课堂导案
B
课堂导案
【例3】已知三角形的两边为3和4,则第三边a的取值范围是__________.
【解析】根据三角形的三边关系,得4-3<a<4+3,即1<a<7.
【答案】1<a<7.
【点拔】已知两边的值,则第三边的范围是:大于两边的差,而小于两边的和.
1<a<7
课堂导案
5. 下列长度的各组线段,可以组成三角形的
是( )
A. 1,2,3 B. 3,3,6
C. 2,4,6 D. 4,5,8
6.三角形的三边长分别为5,8,x,则第三
边长x的取值范围是( )
A.3<x<8 B. 5<x<13
C.3<x<13 D. 8<x<13
D
C
7.一个等腰三角形的两边长分别为2和5,
则它的周长为( )
A. 7 B. 9
C. 12 D.9或12
课堂导案
C
课后练案
8.一个三角形的两边长分别是5cm和2cm,则它的第三边不可能是( )
A. 6cm B. 5cm C. 4cm D. 2cm
9.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种 B.2种 C.3种 D.4种
D
C
课后练案
10.已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A. 10 B.13
C. 17 D.13或17
C
11.如下图,图中有______个三角形,把它们用符号分别表示为_______________________________________,在△BCD中,CD边所对的角是__________.
课后练案
第11题
第12题
12.如上图,以∠C为一个内角的三角形是_________ ______,△AED的三个内角是________________________.
5
△ABC、△EBC、△ABD、△CDE、△BCD
∠DBC
△ABC、 △ ACD、
△ACE
∠ADE、∠AED、∠DAE
课后练案
13.若△ABC的三条边长分别为6,7,x,则x的取值范围是_____________.
14.一个三角形两边长分别为3和8,第三边长为奇数,则第三边长为__________.
1<x<3
7或9
15.已知等腰三角形的周长是16cm.
(1)若其中一边长为6cm,求另外两边长;
(2)若其中一边长为4cm,求另外两边长.
课后练案
6cm、4cm或5cm、5cm
6cm、6cm
16.已知,三角形三边的比是3∶4∶5,且最大边长与最小边长的差是4,求这个三角形的三条边的长.
课后练案
解:设三角形的三边分别为3x、4x、5x,根据题意有:5x-3x=4,解得x=2,3x=6,4x=8,5x=10.答:三角形三边长分别为6;8;10.
17.已知,在△ABC中,AB=8,且BC=2a+2,AC=22,
(1)求a的取值范围;
课后练案
由题意,得22-8<2a+2<22+8,解得6<a<14.
课后练案
(2)若△ABC为等腰三角形,求这个三角形的周长.
△ABC为等腰三角形,则2a+2=8或2a+2=22,解得a=3或a=10,
∵6<a<14,∴a=10,
∴△ABC的周长为22+22+8=52.
能力培优
18.已知:a、b、c是△ABC的三边,且a=4,b=6,若三角形的周长是小于18的偶数.
(1)求c边的长;
由条件得6-4<c<6+4,∴2<c<10,∴12<△ABC的周长<22,又因为△ABC的周长是小于18的偶数,∴△ABC的周长为14或16,当△ABC的周长为14时,c=4,当△ABC的周长为16时,c=6.
能力培优
(2)判断△ABC的形状.
当c=4时,a=c;当c=6时,b=c,所以△ABC是等腰三角形.
感谢聆听
