人教版八年级上册数学11.1.2 三角形的高、中线与角平分线 11.1.3 三角形的稳定性同步课件(2课时 22张)
文档属性
| 名称 | 人教版八年级上册数学11.1.2 三角形的高、中线与角平分线 11.1.3 三角形的稳定性同步课件(2课时 22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 11:01:11 | ||
图片预览






文档简介
三角形
?
第十一章
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
理解三角形的高、中线与角平分线等概念.会用工具画三角形的高、中线与角平分线.了解三角形的稳定性.
课前学案
1.从三角形的一个顶点向它的对边所在直线画垂线,顶点和__________之间的线段叫三角形的高.
2.在三角形中,连接一个顶点和它的对边的__________的线段叫三角形的中线.
垂足
中点
3.三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫_____________________.
4.三角形三条中线的交点叫做三角形的________.
5.三角形的三边确定了,那么它的形状、大小就不会__________,三角形的这个性质叫做________.
三角形的角平分线
重心
改变
稳定性
课前学案
课堂导案
【例1】以下是四位同学在钝角三角形ABC
中画BC边上的高,其中画法正确的是
( )
A. B.
C. D.
B
【解析】找到经过顶点A且与BC垂直的AD所在的图形即可.
【答案】B
【点拔】过三角形的一个顶点向对边引垂线,
顶点和垂足间的线段叫做三角形的
高.
课堂导案
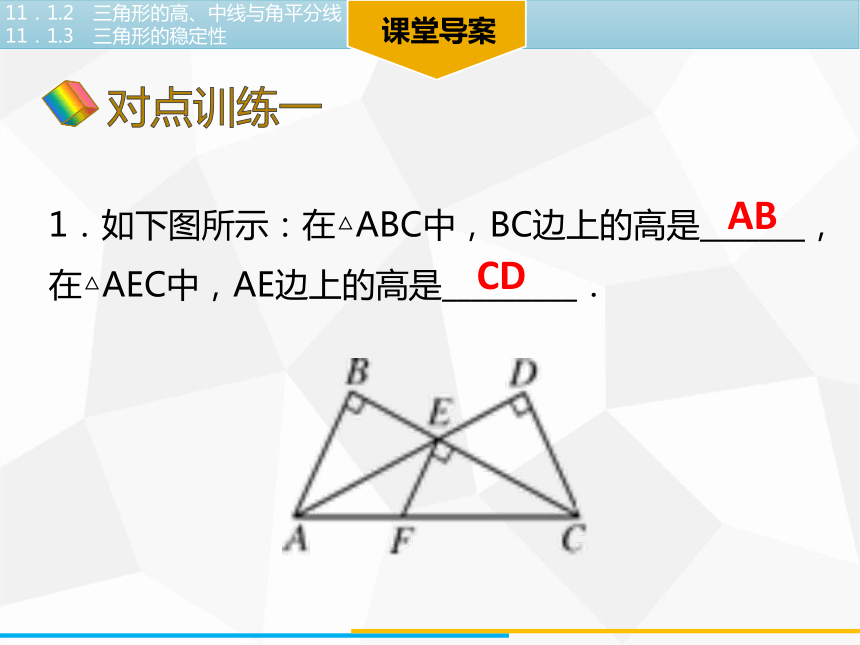
1.如下图所示:在△ABC中,BC边上的高是_______,在△AEC中,AE边上的高是_________.
AB
CD
课堂导案
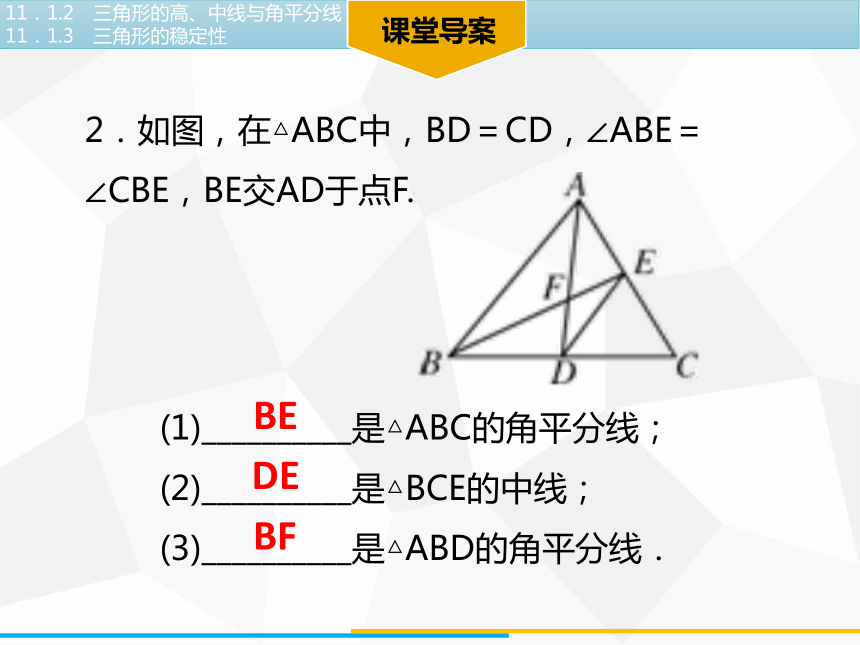
2.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
BE
DE
BF
课堂导案
(1)__________是△ABC的角平分线;
(2)__________是△BCE的中线;
(3)__________是△ABD的角平分线.
∠CAD
3.如下图,在△ABC,AE是中线,AD是角平分线,AF是高,填空:
(1)∠BAD=__________= _________;
(2)BE=__________= __________;
(3)∠AFB=∠AFC=__________;
(4)S△ABC=__________.
∠BAC
CE
BC
90°
?BC?AF
1
2
1
2
课堂导案
【例2】如右图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A. 两点之间的线段最短
B. 两点确定一条直线
C. 三角形有稳定性
D. 长方形的四个角都是直角
【解析】因为四边形不具有稳定性,所以四边形门框容易变形, 钉上根斜木条后,利用了三角形的稳定性.
课堂导案
C
【答案】C
【点拔】四边形不具有稳定性,三角形具有稳定性.
课堂导案
4.下列图形具有稳定性的是( )
A.正方形 B.三角形
C.长方形 D.平行四边形
B
课堂导案
5.如下图,一扇窗户打开后,用窗钩AB可将其固定,
这里所运用的几何原理是( )
A.三角形的稳定性
B.两点之间线段最短
C.两点确定一条直线
D.垂线段最短
A
课堂导案
6.下列图形中,不具有稳定性的是( )
A. B.
C. D.
B
课堂导案
7.三角形的高、中线和角平分线都是( )
A.直线 B.射线
C.线段 D.以上答案都不对
8.下列不是利用三角形稳定性的是( )
A.伸缩晾衣架
B.三角形房架
C.自行车的三角形车架
D.矩形门框的斜拉条
课后练案
C
A
9.若H是△ABC三条高AD、BE、CF的交点,则△HBC中BC边上的高是_____,△BHA中BH边上的高是_____.
DH
第9题
第10题
第11题
AE
2
3
11.要使六边形木架不变形,至少要钉上_____根木条.
10.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是______.
课后练案
12.在下列图中,分别画出三角形BC边上的高.
课后练案
13.如下图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
54
10.8
课后练案
14.如下图,D是△ABC的BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD.
求证:AD是△ABC的角平分线.
∵DE∥AC,∴∠EDA=∠CAD,又∠EDA=∠EAD,∴∠CAD=∠EAD,∴AD是△ABC的角平分线.
课后练案
能力培优
15.如下图,△ABC中,D、E分别是BC、AD的中点,且三角形ABC的面积为4,求阴影部分的面积.
∵BD=CD,∴S△ABD=S△ACD= S△ABC=2,
∵AE=DE,∴S△ACE=S△CDE= S△ACD=1.
感谢聆听
?
第十一章
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
理解三角形的高、中线与角平分线等概念.会用工具画三角形的高、中线与角平分线.了解三角形的稳定性.
课前学案
1.从三角形的一个顶点向它的对边所在直线画垂线,顶点和__________之间的线段叫三角形的高.
2.在三角形中,连接一个顶点和它的对边的__________的线段叫三角形的中线.
垂足
中点
3.三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫_____________________.
4.三角形三条中线的交点叫做三角形的________.
5.三角形的三边确定了,那么它的形状、大小就不会__________,三角形的这个性质叫做________.
三角形的角平分线
重心
改变
稳定性
课前学案
课堂导案
【例1】以下是四位同学在钝角三角形ABC
中画BC边上的高,其中画法正确的是
( )
A. B.
C. D.
B
【解析】找到经过顶点A且与BC垂直的AD所在的图形即可.
【答案】B
【点拔】过三角形的一个顶点向对边引垂线,
顶点和垂足间的线段叫做三角形的
高.
课堂导案
1.如下图所示:在△ABC中,BC边上的高是_______,在△AEC中,AE边上的高是_________.
AB
CD
课堂导案
2.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
BE
DE
BF
课堂导案
(1)__________是△ABC的角平分线;
(2)__________是△BCE的中线;
(3)__________是△ABD的角平分线.
∠CAD
3.如下图,在△ABC,AE是中线,AD是角平分线,AF是高,填空:
(1)∠BAD=__________= _________;
(2)BE=__________= __________;
(3)∠AFB=∠AFC=__________;
(4)S△ABC=__________.
∠BAC
CE
BC
90°
?BC?AF
1
2
1
2
课堂导案
【例2】如右图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A. 两点之间的线段最短
B. 两点确定一条直线
C. 三角形有稳定性
D. 长方形的四个角都是直角
【解析】因为四边形不具有稳定性,所以四边形门框容易变形, 钉上根斜木条后,利用了三角形的稳定性.
课堂导案
C
【答案】C
【点拔】四边形不具有稳定性,三角形具有稳定性.
课堂导案
4.下列图形具有稳定性的是( )
A.正方形 B.三角形
C.长方形 D.平行四边形
B
课堂导案
5.如下图,一扇窗户打开后,用窗钩AB可将其固定,
这里所运用的几何原理是( )
A.三角形的稳定性
B.两点之间线段最短
C.两点确定一条直线
D.垂线段最短
A
课堂导案
6.下列图形中,不具有稳定性的是( )
A. B.
C. D.
B
课堂导案
7.三角形的高、中线和角平分线都是( )
A.直线 B.射线
C.线段 D.以上答案都不对
8.下列不是利用三角形稳定性的是( )
A.伸缩晾衣架
B.三角形房架
C.自行车的三角形车架
D.矩形门框的斜拉条
课后练案
C
A
9.若H是△ABC三条高AD、BE、CF的交点,则△HBC中BC边上的高是_____,△BHA中BH边上的高是_____.
DH
第9题
第10题
第11题
AE
2
3
11.要使六边形木架不变形,至少要钉上_____根木条.
10.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是______.
课后练案
12.在下列图中,分别画出三角形BC边上的高.
课后练案
13.如下图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
54
10.8
课后练案
14.如下图,D是△ABC的BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD.
求证:AD是△ABC的角平分线.
∵DE∥AC,∴∠EDA=∠CAD,又∠EDA=∠EAD,∴∠CAD=∠EAD,∴AD是△ABC的角平分线.
课后练案
能力培优
15.如下图,△ABC中,D、E分别是BC、AD的中点,且三角形ABC的面积为4,求阴影部分的面积.
∵BD=CD,∴S△ABD=S△ACD= S△ABC=2,
∵AE=DE,∴S△ACE=S△CDE= S△ACD=1.
感谢聆听
