人教版八年级上册数学 11.2.1 三角形的内角同步课件(23张)
文档属性
| 名称 | 人教版八年级上册数学 11.2.1 三角形的内角同步课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览





文档简介
三角形
?
第十一章
11.2.1 三角形的内角
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
掌握三角形内角和定理及其推理过程,能应用三角形内角和定理解决一些简单的实际问题.
课前学案
1.三角形的内角和等于________.
2.直角三角形的两个锐角_________.
3.有两个角互余的三角形是_____________.
180°
互余
直角三角形
课堂导案
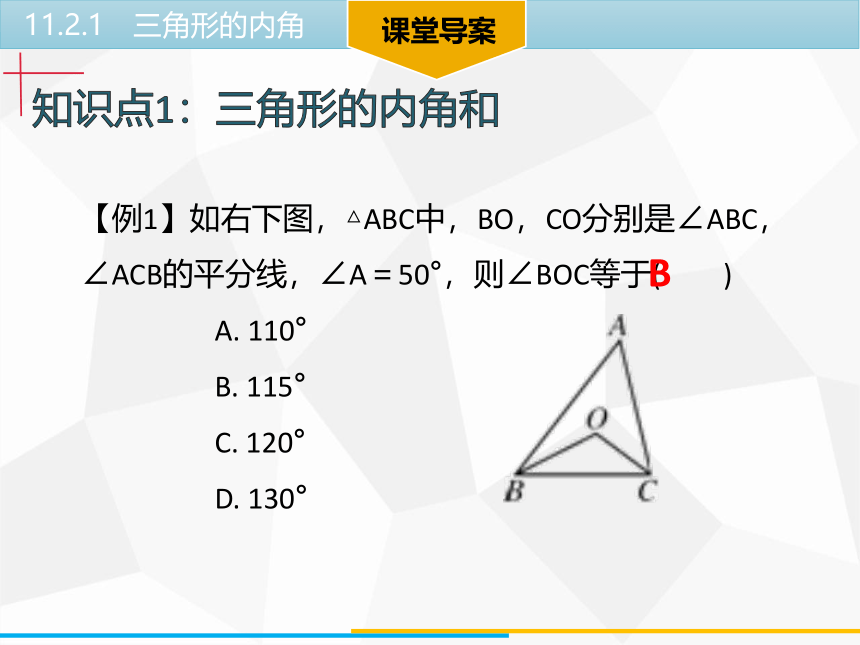
【例1】如右下图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
A. 110°
B. 115°
C. 120°
D. 130°
B
课堂导案
【解析】由三角形内角和定理和角平分线的定义求出∠OBC+ ∠OCB的度数,再根据三角形的内角和等于180°即可求出∠BOC的度数.
【答案】B
【点拔】本题主要利用三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.
课堂导案
1.在△ABC中,∠A=30°,∠B=45°,则∠C=
__________.
2.在△ABC中,∠A+∠B=110°,则∠C=______.
3.在△ABC中,∠A=120°,∠B=∠C,则∠C=
_________.
4.△ABC中,∠A=∠B=2∠C,则∠A=________.
105°
70°
30°
72°
课堂导案
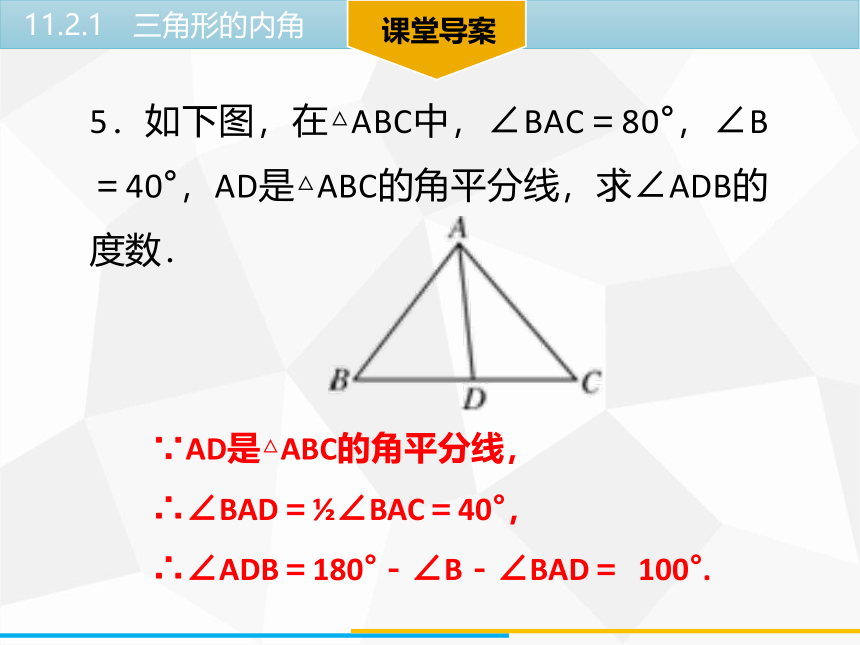
5.如下图,在△ABC中,∠BAC=80°,∠B=40°,AD是△ABC的角平分线,求∠ADB的度数.
∵AD是△ABC的角平分线,
∴∠BAD=?∠BAC=40°,
∴∠ADB=180°-∠B-∠BAD= 100°.
课堂导案
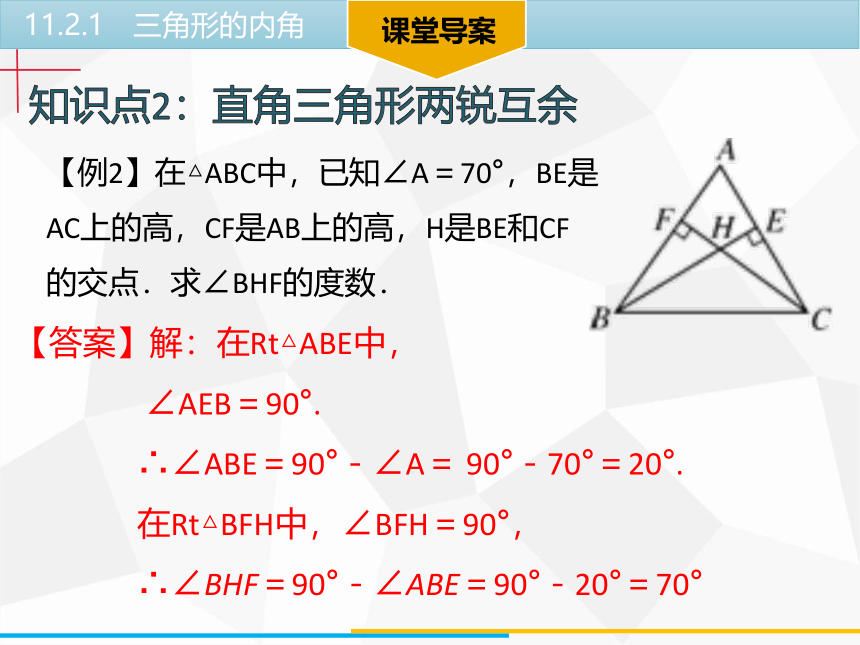
【例2】在△ABC中,已知∠A=70°,BE是
AC上的高,CF是AB上的高,H是BE和CF
的交点.求∠BHF的度数.
【答案】解:在Rt△ABE中,
∠AEB=90°.
∴∠ABE=90°-∠A= 90°-70°=20°.
在Rt△BFH中,∠BFH=90°,
∴∠BHF=90°-∠ABE=90°-20°=70°
课堂导案
【点拔】本题熟知“直角三角形的两个锐角互余”是解答此题的关键.
【解析】在Rt△ABE中,求出∠ABE的度数,然后在Rt△BFH中,根据∠ABE与∠BHF的互余关系则可求解.
课堂导案
6.在Rt△ABC中,∠C=90°,∠A=40°,则∠B=_____.
7.已知:如下图,△ABC中,∠ACB=90°,CD⊥AB,垂
足为D,∠1=65°,则∠B=______度.
第7题 第8题
8.如上图,AB∥CD,AC⊥BC,∠BAC=55°,则∠BCD
的度数为________.
50°
65
35°
课堂导案
9.如下图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.
(1)求∠EAC的度数;
∠EAC=90°-∠C=90°-70°=20°
(2)求∠ADE的度数.
课堂导案
∠BAC=180°-∠B-∠C=80°,
∵AD为△ABC的角平分线,
∴∠DAC= ∠BAC=40°,
∴∠ADE=180°-∠C-∠DAC=70°.
11.如上图,将一副三角板按图中的方式叠放,则角α等于________度.
课后练案
10.如下图,AB∥CD,AC与BD相交于点O,∠A=30°,∠COD=105°.则∠D=________度.
第10题
第11题
45
75
13.如上图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是_________.
课后练案
12.如下图,AE是△ABC的边BC上的高,AD平分∠EAC,∠C=44°,则∠ADE=________度.
67
135°
第12题
第13题
14.如下图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
课后练案
在Rt△BCE中,∠BEC=90°,
∴∠B=90°-∠BCE=50°,
∵AD平分∠BAC,
∴∠BAD= ∠BAC=30°,
∴∠ADB=180°-∠B-∠BAD=100°.
15.如下图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
课后练案
∠BAC=180°-∠B-∠C=60°,
∵AD平分∠BAC,
∴∠BAD= ∠BAC=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
课后练案
(2)若DE⊥AC于点E,求∠ADE的度数.
∵∠CAD= ∠BAC=30°,
∴∠ADE=90°-∠CAD=60°.
16.如下图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
课后练案
设∠A=x°,则∠C=∠ABC=2x°,由三角形内角和定理,
得x+2x+2x=180,解得x=36,∴∠C=72°,∵BD⊥AC,∴∠DBC=90°-∠C=18°.
课后练案
17.如下图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点
在C处的北偏西55°方向,求
∠BCA及∠BAC的度数.
由题意,得∠DBA=40°,∠DBC=85°,
∴∠ABC=∠DBC-∠DBA=45°,∵DB∥EC,∴∠BCE=180°-∠DBC=95°,∵∠ACE=55°,∴∠BCA=∠BCE-∠ACE=40°, ∴∠BAC=180°-∠ABC-∠BCA=95°.
能力培优
18.已知,如下图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=40°,∠C=30°,则∠DAE=________;
(2)若∠B=80°,∠C=40°,则∠DAE=________;
(3)请你由(1)、(2)猜想∠DAE与∠B、∠C有何数量关系?并证明你的猜想.
5°
20°
能力培优
∠DAE= (∠B-∠C),
证明:∵AE平分∠BAC,∴∠CAE=∠∠BAC
∵∠BAC=180°-(∠B+∠C),
∴∠CAE=90°- (∠B+∠C),
∵AD⊥BC,∴∠DAC=90°-∠C,
∴∠DAE=∠DAC-∠CAE=(90°-∠C)-
= (∠B+∠C)-∠C= (∠B-∠C).
感谢聆听
?
第十一章
11.2.1 三角形的内角
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
掌握三角形内角和定理及其推理过程,能应用三角形内角和定理解决一些简单的实际问题.
课前学案
1.三角形的内角和等于________.
2.直角三角形的两个锐角_________.
3.有两个角互余的三角形是_____________.
180°
互余
直角三角形
课堂导案
【例1】如右下图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
A. 110°
B. 115°
C. 120°
D. 130°
B
课堂导案
【解析】由三角形内角和定理和角平分线的定义求出∠OBC+ ∠OCB的度数,再根据三角形的内角和等于180°即可求出∠BOC的度数.
【答案】B
【点拔】本题主要利用三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.
课堂导案
1.在△ABC中,∠A=30°,∠B=45°,则∠C=
__________.
2.在△ABC中,∠A+∠B=110°,则∠C=______.
3.在△ABC中,∠A=120°,∠B=∠C,则∠C=
_________.
4.△ABC中,∠A=∠B=2∠C,则∠A=________.
105°
70°
30°
72°
课堂导案
5.如下图,在△ABC中,∠BAC=80°,∠B=40°,AD是△ABC的角平分线,求∠ADB的度数.
∵AD是△ABC的角平分线,
∴∠BAD=?∠BAC=40°,
∴∠ADB=180°-∠B-∠BAD= 100°.
课堂导案
【例2】在△ABC中,已知∠A=70°,BE是
AC上的高,CF是AB上的高,H是BE和CF
的交点.求∠BHF的度数.
【答案】解:在Rt△ABE中,
∠AEB=90°.
∴∠ABE=90°-∠A= 90°-70°=20°.
在Rt△BFH中,∠BFH=90°,
∴∠BHF=90°-∠ABE=90°-20°=70°
课堂导案
【点拔】本题熟知“直角三角形的两个锐角互余”是解答此题的关键.
【解析】在Rt△ABE中,求出∠ABE的度数,然后在Rt△BFH中,根据∠ABE与∠BHF的互余关系则可求解.
课堂导案
6.在Rt△ABC中,∠C=90°,∠A=40°,则∠B=_____.
7.已知:如下图,△ABC中,∠ACB=90°,CD⊥AB,垂
足为D,∠1=65°,则∠B=______度.
第7题 第8题
8.如上图,AB∥CD,AC⊥BC,∠BAC=55°,则∠BCD
的度数为________.
50°
65
35°
课堂导案
9.如下图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.
(1)求∠EAC的度数;
∠EAC=90°-∠C=90°-70°=20°
(2)求∠ADE的度数.
课堂导案
∠BAC=180°-∠B-∠C=80°,
∵AD为△ABC的角平分线,
∴∠DAC= ∠BAC=40°,
∴∠ADE=180°-∠C-∠DAC=70°.
11.如上图,将一副三角板按图中的方式叠放,则角α等于________度.
课后练案
10.如下图,AB∥CD,AC与BD相交于点O,∠A=30°,∠COD=105°.则∠D=________度.
第10题
第11题
45
75
13.如上图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是_________.
课后练案
12.如下图,AE是△ABC的边BC上的高,AD平分∠EAC,∠C=44°,则∠ADE=________度.
67
135°
第12题
第13题
14.如下图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
课后练案
在Rt△BCE中,∠BEC=90°,
∴∠B=90°-∠BCE=50°,
∵AD平分∠BAC,
∴∠BAD= ∠BAC=30°,
∴∠ADB=180°-∠B-∠BAD=100°.
15.如下图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
课后练案
∠BAC=180°-∠B-∠C=60°,
∵AD平分∠BAC,
∴∠BAD= ∠BAC=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
课后练案
(2)若DE⊥AC于点E,求∠ADE的度数.
∵∠CAD= ∠BAC=30°,
∴∠ADE=90°-∠CAD=60°.
16.如下图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
课后练案
设∠A=x°,则∠C=∠ABC=2x°,由三角形内角和定理,
得x+2x+2x=180,解得x=36,∴∠C=72°,∵BD⊥AC,∴∠DBC=90°-∠C=18°.
课后练案
17.如下图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点
在C处的北偏西55°方向,求
∠BCA及∠BAC的度数.
由题意,得∠DBA=40°,∠DBC=85°,
∴∠ABC=∠DBC-∠DBA=45°,∵DB∥EC,∴∠BCE=180°-∠DBC=95°,∵∠ACE=55°,∴∠BCA=∠BCE-∠ACE=40°, ∴∠BAC=180°-∠ABC-∠BCA=95°.
能力培优
18.已知,如下图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=40°,∠C=30°,则∠DAE=________;
(2)若∠B=80°,∠C=40°,则∠DAE=________;
(3)请你由(1)、(2)猜想∠DAE与∠B、∠C有何数量关系?并证明你的猜想.
5°
20°
能力培优
∠DAE= (∠B-∠C),
证明:∵AE平分∠BAC,∴∠CAE=∠∠BAC
∵∠BAC=180°-(∠B+∠C),
∴∠CAE=90°- (∠B+∠C),
∵AD⊥BC,∴∠DAC=90°-∠C,
∴∠DAE=∠DAC-∠CAE=(90°-∠C)-
= (∠B+∠C)-∠C= (∠B-∠C).
感谢聆听
