人教版八年级上册数学 11.2.2 三角形的外角同步课件(19张)
文档属性
| 名称 | 人教版八年级上册数学 11.2.2 三角形的外角同步课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 07:03:44 | ||
图片预览




文档简介
三角形
?
第十一章
11.2.2 三角形的外角
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解三角形外角的概念,掌握三角形的外角的性质,能利用三角形的外角的性质计算三角形相关的角.
课前学案
1.三角形的一边与另一边的__________组成的角,叫做三角形的外角.
2.三角形的外角__________与它不相邻的两个内角的和.
3.三角形的外角和等于___________.
延长线
等于
360°
课堂导案
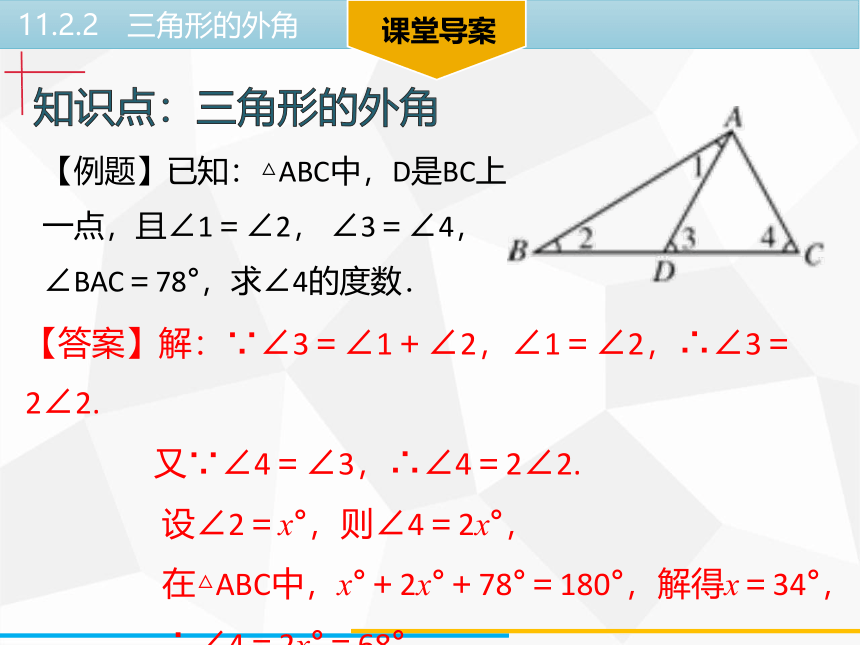
【例题】已知:△ABC中,D是BC上
一点,且∠1=∠2, ∠3=∠4,
∠BAC=78°,求∠4的度数.
【答案】解:∵∠3=∠1+∠2,∠1=∠2,∴∠3=2∠2.
又∵∠4=∠3,∴∠4=2∠2.
设∠2=x°,则∠4=2x°,
在△ABC中,x°+2x°+78°=180°,解得x=34°,
∴∠4=2x°=68°.
课堂导案
【点拔】本题考查三角形外角的性质及三角形 的内角和定 理.求角的度数常常要用到“三角形的内角和是180°” 这一隐含的条件;以及三角形的一个外角等于与它不相邻的两个内角的和.
【解析】运用三角形外角的性质建立∠3,∠4与∠1,∠2 的关系,再利用三角形内角和定理借助方程思想 求解.
课堂导案
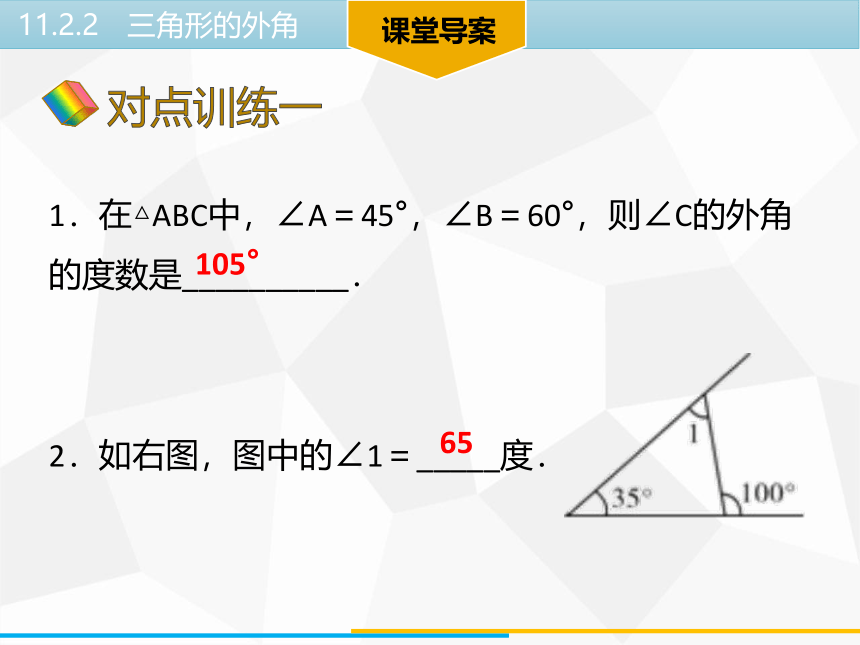
1.在△ABC中,∠A=45°,∠B=60°,则∠C的外角的度数是__________.
2.如右图,图中的∠1=_____度.
105°
65
课堂导案
3.将一副三角板按图中方式叠放,则角α=_____度.
第3题 第4题
4.如上图所示,则α=_______.
75
114°
课堂导案
5.将一副直角三角尺如下图放置,已知AE∥BC,求∠AFD的度数.
∵AE∥BC,∴∠FDC=∠E=45°,
∴∠AFD=∠C+∠FDC=75°.
课后练案
6.如下图,已知直线AB∥CD,∠A=25°,∠E=85°,则∠C=__________度.
第6题
第7题
7.如上图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2=__________.
110
101°
课后练案
8.如下图,点B、C、D在同一条直线上,∠A=70°,∠B=60°,∠D=20°,则∠CED=_______.
9.如上图,点D、E为△ABC边BC、AC上的两点,将△ABC沿线段DE折叠,点C落在BD上的C′处,若∠C=30°,则∠AEC′=__________.
第8题
第9题
30°
60°
课后练案
10.如下图,△ABC中,∠C=90°,两个锐角的平分线相交于点D,则∠ADE=__________度.
11.如上图,若检验工人量得一个零件的∠A=90°,∠B=32°,∠C=21°,则∠BDC=_________度.
第10题
第11题
45
143
课后练案
12.如下图,若∠A=70°,∠ACD=40°,∠ABE=30°,求∠BDC,
∠BFC的度数.
∠BDC=∠A+∠ACD=110°,
∠BFC=∠ABE+∠BDC=140°.
课后练案
13.如下图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
∵DF⊥AB,
∴∠BFD=90°,
∴∠B=90°-∠D=48°,
∴∠ACD=∠B+∠A=83°.
课后练案
14.如下图,AD是△ABC的外角∠CAE的平分线,∠B=30°,∠DAE=55°.求:
(1)∠D的度数;
(2)∠ACD的度数.
∠D=∠DAE-∠B
=55°-30°=25°.
∵AD平分∠CAE,∴∠CAD=∠DAE=55°,∴∠ACD=180°-∠CAD-∠D=100°.
课后练案
15.在△ABC中,∠B=∠C=∠BAD,∠ADC=∠DAC,求∠ADC的度数.
设∠B=∠C=∠BAD=x°,
则∠ADC=∠DAC=∠B+∠BAD=2x°,∴2x+2x+x=180,解得x=36,
∴∠ADC=2x°=72°.
能力培优
16.如下图,在△ABC中,∠ABC的平分线与∠C的外角平分线相交于D.
(1)若∠A=40°,则∠D=__________;
(2)若∠A=60°,则∠D=__________;
(3)猜想∠A与∠D的数量关系,并证明你的猜想.
20°
30°
能力培优
∠A=2∠D,证明:
∵BD、CD分别平分∠ABC、∠ACE,
∴∠ABC=2∠3,∠ACE=2∠1,
∴∠A=∠ACE-∠ABC=2∠1-2∠3=2(∠1-∠3),
∵∠D=∠1-∠3,
∴∠A=2∠D.
感谢聆听
?
第十一章
11.2.2 三角形的外角
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解三角形外角的概念,掌握三角形的外角的性质,能利用三角形的外角的性质计算三角形相关的角.
课前学案
1.三角形的一边与另一边的__________组成的角,叫做三角形的外角.
2.三角形的外角__________与它不相邻的两个内角的和.
3.三角形的外角和等于___________.
延长线
等于
360°
课堂导案
【例题】已知:△ABC中,D是BC上
一点,且∠1=∠2, ∠3=∠4,
∠BAC=78°,求∠4的度数.
【答案】解:∵∠3=∠1+∠2,∠1=∠2,∴∠3=2∠2.
又∵∠4=∠3,∴∠4=2∠2.
设∠2=x°,则∠4=2x°,
在△ABC中,x°+2x°+78°=180°,解得x=34°,
∴∠4=2x°=68°.
课堂导案
【点拔】本题考查三角形外角的性质及三角形 的内角和定 理.求角的度数常常要用到“三角形的内角和是180°” 这一隐含的条件;以及三角形的一个外角等于与它不相邻的两个内角的和.
【解析】运用三角形外角的性质建立∠3,∠4与∠1,∠2 的关系,再利用三角形内角和定理借助方程思想 求解.
课堂导案
1.在△ABC中,∠A=45°,∠B=60°,则∠C的外角的度数是__________.
2.如右图,图中的∠1=_____度.
105°
65
课堂导案
3.将一副三角板按图中方式叠放,则角α=_____度.
第3题 第4题
4.如上图所示,则α=_______.
75
114°
课堂导案
5.将一副直角三角尺如下图放置,已知AE∥BC,求∠AFD的度数.
∵AE∥BC,∴∠FDC=∠E=45°,
∴∠AFD=∠C+∠FDC=75°.
课后练案
6.如下图,已知直线AB∥CD,∠A=25°,∠E=85°,则∠C=__________度.
第6题
第7题
7.如上图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2=__________.
110
101°
课后练案
8.如下图,点B、C、D在同一条直线上,∠A=70°,∠B=60°,∠D=20°,则∠CED=_______.
9.如上图,点D、E为△ABC边BC、AC上的两点,将△ABC沿线段DE折叠,点C落在BD上的C′处,若∠C=30°,则∠AEC′=__________.
第8题
第9题
30°
60°
课后练案
10.如下图,△ABC中,∠C=90°,两个锐角的平分线相交于点D,则∠ADE=__________度.
11.如上图,若检验工人量得一个零件的∠A=90°,∠B=32°,∠C=21°,则∠BDC=_________度.
第10题
第11题
45
143
课后练案
12.如下图,若∠A=70°,∠ACD=40°,∠ABE=30°,求∠BDC,
∠BFC的度数.
∠BDC=∠A+∠ACD=110°,
∠BFC=∠ABE+∠BDC=140°.
课后练案
13.如下图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
∵DF⊥AB,
∴∠BFD=90°,
∴∠B=90°-∠D=48°,
∴∠ACD=∠B+∠A=83°.
课后练案
14.如下图,AD是△ABC的外角∠CAE的平分线,∠B=30°,∠DAE=55°.求:
(1)∠D的度数;
(2)∠ACD的度数.
∠D=∠DAE-∠B
=55°-30°=25°.
∵AD平分∠CAE,∴∠CAD=∠DAE=55°,∴∠ACD=180°-∠CAD-∠D=100°.
课后练案
15.在△ABC中,∠B=∠C=∠BAD,∠ADC=∠DAC,求∠ADC的度数.
设∠B=∠C=∠BAD=x°,
则∠ADC=∠DAC=∠B+∠BAD=2x°,∴2x+2x+x=180,解得x=36,
∴∠ADC=2x°=72°.
能力培优
16.如下图,在△ABC中,∠ABC的平分线与∠C的外角平分线相交于D.
(1)若∠A=40°,则∠D=__________;
(2)若∠A=60°,则∠D=__________;
(3)猜想∠A与∠D的数量关系,并证明你的猜想.
20°
30°
能力培优
∠A=2∠D,证明:
∵BD、CD分别平分∠ABC、∠ACE,
∴∠ABC=2∠3,∠ACE=2∠1,
∴∠A=∠ACE-∠ABC=2∠1-2∠3=2(∠1-∠3),
∵∠D=∠1-∠3,
∴∠A=2∠D.
感谢聆听
