2019-2020学年湖南省益阳市桃江县八年级(下)期末数学试卷(word版,含解析)
文档属性
| 名称 | 2019-2020学年湖南省益阳市桃江县八年级(下)期末数学试卷(word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 06:46:46 | ||
图片预览



文档简介
2019-2020学年湖南省益阳市桃江县八年级(下)期末数学试卷
一、选择题(本大题共8个小题,每小题5分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)
1.(5分)直角三角形中,有两边的长分别为3和4,那么第三边的长的平方为( )
A.25 B.14 C.7 D.7或25
2.(5分)下列条件中,不能判定△ABC与△DEF一定全等的是( )
A.AB=DE,BC=EF,∠A=∠D=90°
B.AB=DE,BC=EF,∠A=∠D=80°
C.AB=DE,∠A=∠D=90°,∠B=∠E=40°
D.BC=EF,∠A=∠D=80°,∠B=∠E=40°
3.(5分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6 B.7 C.8 D.9
4.(5分)2020年是我国完成第一个100年奋斗目标的关键之年,到2021年我国全面建成小康社会.人民生活水平越来越高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是( )
A. B. C. D.
5.(5分)在平面直角坐标系中,点P(﹣3,5)向下平移2个单位,再向右平移4个单位,是点Q,那么Q点的坐标是( )
A.(﹣7,7) B.(1,7) C.(1,3) D.(﹣7,3)
6.(5分)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A. B.
C. D.
7.(5分)以下四点:(1,2),(2,3),(0,1),(﹣2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
8.(5分)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
二、填空题(本大题共6个小题,每小题5分,共30分;把答案填在题中的横线上)
9.(5分)在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,CD=2,则BC的长为 .
10.(5分)如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是 .(填上一个即可).
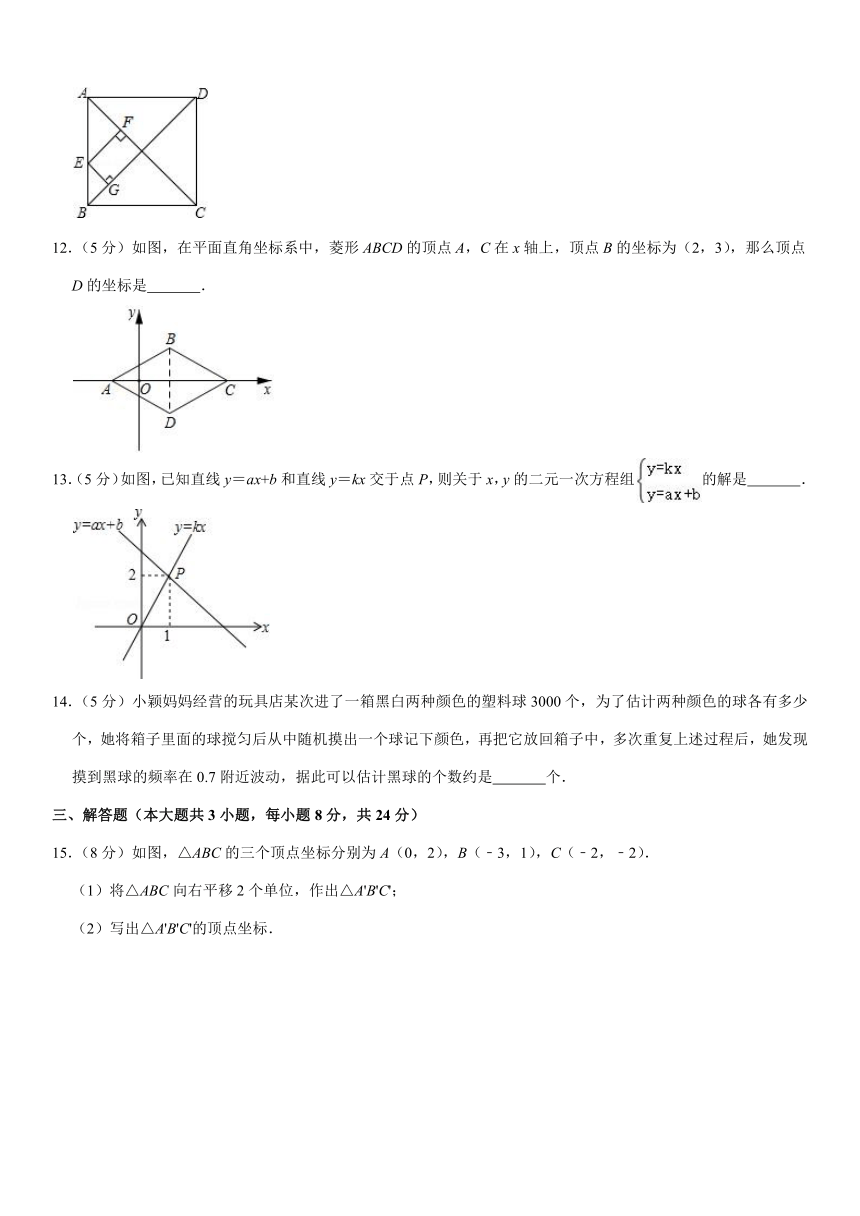
11.(5分)如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
12.(5分)如图,在平面直角坐标系中,菱形ABCD的顶点A,C在x轴上,顶点B的坐标为(2,3),那么顶点D的坐标是 .
13.(5分)如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
14.(5分)小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球的个数约是 个.
三、解答题(本大题共3小题,每小题8分,共24分)
15.(8分)如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).
(1)将△ABC向右平移2个单位,作出△A'B'C';
(2)写出△A'B'C'的顶点坐标.
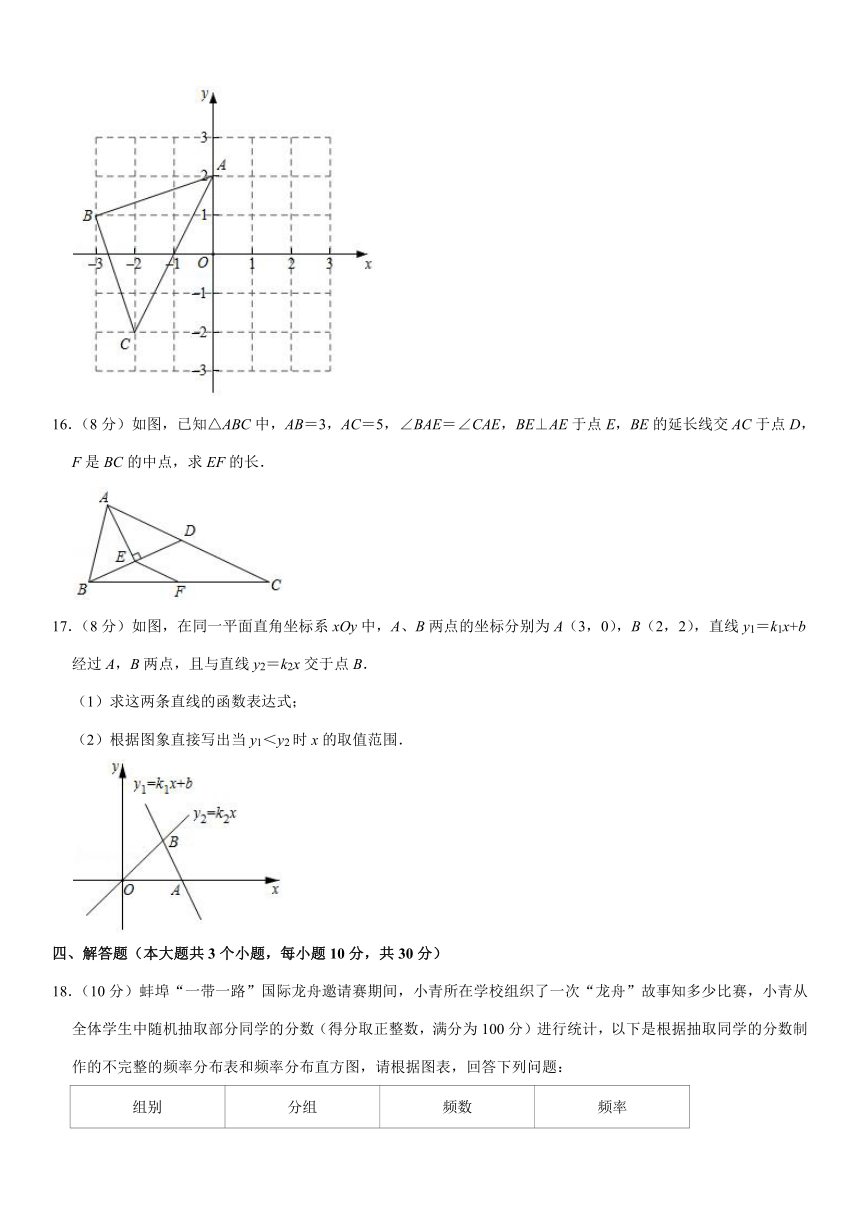
16.(8分)如图,已知△ABC中,AB=3,AC=5,∠BAE=∠CAE,BE⊥AE于点E,BE的延长线交AC于点D,F是BC的中点,求EF的长.
17.(8分)如图,在同一平面直角坐标系xOy中,A、B两点的坐标分别为A(3,0),B(2,2),直线y1=k1x+b经过A,B两点,且与直线y2=k2x交于点B.
(1)求这两条直线的函数表达式;
(2)根据图象直接写出当y1<y2时x的取值范围.
四、解答题(本大题共3个小题,每小题10分,共30分)
18.(10分)蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计,以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题:
组别
分组
频数
频率
1
50≤x<60
9
0.18
2
60≤x<70
m
b
3
70≤x<80
21
0.42
4
80≤x<90
a
0.06
5
90≤x<100
2
n
(1)根据上表填空:a= ,b= ,m= .
(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在90≤x≤100的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
19.(10分)一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
20.(10分)如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE交BC于点F,连接AC,BE;若∠AFC=2∠D,AB=2,BC=4.
(1)求证:四边形ABEC是矩形;
(2)求BE的长.
五、解答题(本题满分10分)
21.(10分)如图,在平面直角坐标系中,已知点A(﹣6,0),B(0,8),点C为OB的中点,点D在第二象限,四边形AOCD为矩形,直线AB交DC于点E.
(1)求直线AB的解析式及点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发沿线段AO以每秒2个单位长度的速度向终点O运动,当其中一点到达终点时,两点同时停止运动.连接NP,设点P的运动时间为t秒.
①当t为何值时,四边形ANPE为平行四边形?
②当t为何值时,四边形ANPD为矩形?
六、解答题(本题满分14分)
22.(14分)AC是菱形ABCD的对角线,∠B=60°,AB=2,∠EAF=60°,将∠EAF绕顶点A旋转,∠EAF的两边分别与直线BC,CD交于点E,F,连接EF.
(1)【感知】如图1,若E,F分别是边BC,CD的中点,则CE+CF= ;
(2)【探究】如图2,若E是线段BC上任意一点,求CE+CF的长;
(3)【应用】如图3,若E是BC延长线上一点,且EF⊥BC,求△AEF的周长.
2019-2020学年湖南省益阳市桃江县八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题5分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)
1.【答案】D
【解答】解:分两种情况:
①当3和4为两条直角边长时,
②当4为斜边长时,
综上所述:第三边长的平方是7或25.
故选:D.
2.【答案】B
【解答】解:A、∵AB=DE,BC=EF,∠A=∠D=90°,∴根据HL证明Rt△ABC≌Rt△DEF,不符合题意;
B、∵AB=DE,BC=EF,∠A=∠D=80°,根据ASS不能推出△ABC≌△DEF,故本选项符合题意;
C、∵AB=DE,∠A=∠D=90°,∠B=∠E=40°,∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;
D、∵BC=EF,∠A=∠D=80°,∠B=∠E=40°,∴利用AAS能推出△ABC≌△DEF,故本选项不符合题意;
故选:B.
3.【答案】D
【解答】解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
故选:D.
4.【答案】A
【解答】解:A、是中心对称图形,符合题意;
B、不是中心对称图形,不合题意;
C、是轴对称图形,不是中心对称图形,不合题意;
D、是轴对称图形,不是中心对称图形,不合题意.
故选:A.
5.【答案】C
【解答】解:点A(﹣3,5)向右平移4个单位长度,再向下平移2个单位长度可得点的坐标(1,2),
故选:C.
6.【答案】D
【解答】解:∵洗衣机工作前洗衣机内无水,
∴A,B两选项不正确,被淘汰;
∴C选项不正确,被淘汰,
故选:D.
7.【答案】A
【解答】解:在y=2x+1中,
当x=1时,代入得y=3,所以点(3,2)不在直线上,
当x=0时,代入得y=1,所以点(0,1)在直线上,
综上可知在直线y=8x+1上的点只有一个,
故选:A.
8.【答案】D
【解答】解:A.得分在70~80分的人数最多,此选项正确;
B.该班的总人数为4+12+14+8+2=40(人),此选项正确;
D.得分及格(≥60)的有12+14+2+2=36人,此选项错误;
故选:D.
二、填空题(本大题共6个小题,每小题5分,共30分;把答案填在题中的横线上)
9.【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2×2=4,
∴BC=AB=2,
故答案为:2.
10.【答案】见试题解答内容
【解答】解:
如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
若AE=CF,则有AO﹣AE=CO﹣CF,即OE=OF,
故答案为:AE=CF.
11.【答案】见试题解答内容
【解答】解:如图:
∴OA=OB=4,
∴OA?OB=OA?EF+OB?EG,
∴EF+EG=4.
故答案为:4.
12.【答案】见试题解答内容
【解答】解:∵菱形ABCD的顶点A,C在x轴上,
∴AC⊥BD,菱形ABCD关于x轴对称,
∵顶点B的坐标为(2,3),
故答案为:(2,﹣3).
13.【答案】见试题解答内容
【解答】解:∵直线y=ax+b和直线y=kx交点P的坐标为(1,2),
∴关于x,y的二元一次方程组的解为.
故答案为.
14.【答案】见试题解答内容
【解答】解:设黑球的个数为x,
∵黑球的频率在0.7附近波动,∴摸出黑球的概率为0.7,即=0.2,解得x=2100个.
三、解答题(本大题共3小题,每小题8分,共24分)
15.【答案】见试题解答内容
【解答】解:(1)如图,△A'B'C'即为所求.
(2)A′(2,2),B′(﹣1,1),C′(5,﹣2).
16.【答案】1.
【解答】解:在△AEB和△AED中,
,
∴AD=AB=3,BE=ED,
∵BE=ED,BF=FC,
∴EF=CD=1.
17.【答案】见试题解答内容
【解答】解:(1)∵直线y1=k1x+b经过A,B两点,A(3,0),B(4,2),
∴,解得,
∵直线y2=k2x经过点B.
解得k2=1,
∴这两条直线的函数表达式为y7=﹣2x+6和y2=x;
(2)由图象可知,当x>2时,y1<y5.
四、解答题(本大题共3个小题,每小题10分,共30分)
18.【答案】见试题解答内容
【解答】解:(1)9÷0.18=50(人).
a=50×0.06=4,m=50﹣(9+21+3+2)=15,b=15÷50=0.7.
(2)全班共有50名学生,中位数是第25、26个数据的平均数,第25、26个数据在第3组,
(7)×600=24(人).
答:共有24名学生被选拔参加决赛.
19.【答案】见试题解答内容
【解答】解:(1)设当4≤x≤12时的直线方程为:y=kx+b(k≠0).
∵图象过(6,20)、(12,30),
解得:,
(2)根据图象,每分钟进水20÷4=5升,
解得:m=.
故每分钟进水、出水各是5升、升.
20.【答案】见试题解答内容
【解答】(1)证明;∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠ABC=∠D,
∴AB=CE,
∴BC=2BF,AE=2AF,
∴∠ABC=∠BAE,
∴AE=BC,
(2)解:∵四边形ABEC是矩形,
∴BE===7.
五、解答题(本题满分10分)
21.【答案】见试题解答内容
【解答】解:(1)设直线AB的解析式为:y=kx+b,
将点A(﹣6,0),点B(0,8)代入y=kx+b得:,
∴直线AB的解析式为:y=x+8,
∴C(0,4),
∴CD∥OA,
将y=4代入y=x+8得:x=﹣3,
(2)①∵四边形AOCD为矩形,
∴当EP=AN时,四边形ANPE为平行四边形,
∴t=1,
②∵四边形AOCD为矩形,
∴当DP=AN时,四边形ANPD为矩形,
∴t=5,
∴当t=2s时,四边形ANPD为矩形.
六、解答题(本题满分14分)
22.【答案】见试题解答内容
【解答】解:(1)∵四边形ABCD是菱形,
∴BC=CD=AB=2,
∴CE=BC,CF=CD=1,
故答案为:2.
∴AB=BC,∠B+∠BCD=180°,
∴△ABC是等边三角形,∠ACB=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴△ABE≌△ACF(ASA),
∴CE+CF=CE+BE=BC=3;
∴AE=AF,CE=DF,
∴△AEF是等边三角形,
∵AB∥FC,∠FCE=∠B=60°,∠CEF=90°,
即CD+DF=2CE,CE=2,CF=4,
∴△AEF的周长为6.
一、选择题(本大题共8个小题,每小题5分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)
1.(5分)直角三角形中,有两边的长分别为3和4,那么第三边的长的平方为( )
A.25 B.14 C.7 D.7或25
2.(5分)下列条件中,不能判定△ABC与△DEF一定全等的是( )
A.AB=DE,BC=EF,∠A=∠D=90°
B.AB=DE,BC=EF,∠A=∠D=80°
C.AB=DE,∠A=∠D=90°,∠B=∠E=40°
D.BC=EF,∠A=∠D=80°,∠B=∠E=40°
3.(5分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6 B.7 C.8 D.9
4.(5分)2020年是我国完成第一个100年奋斗目标的关键之年,到2021年我国全面建成小康社会.人民生活水平越来越高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是( )
A. B. C. D.
5.(5分)在平面直角坐标系中,点P(﹣3,5)向下平移2个单位,再向右平移4个单位,是点Q,那么Q点的坐标是( )
A.(﹣7,7) B.(1,7) C.(1,3) D.(﹣7,3)
6.(5分)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A. B.
C. D.
7.(5分)以下四点:(1,2),(2,3),(0,1),(﹣2,3)在直线y=2x+1上的有( )
A.1个 B.2个 C.3个 D.4个
8.(5分)某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的得分段的频数为2
D.得分及格(≥60)的有12人
二、填空题(本大题共6个小题,每小题5分,共30分;把答案填在题中的横线上)
9.(5分)在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,CD=2,则BC的长为 .
10.(5分)如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是 .(填上一个即可).
11.(5分)如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
12.(5分)如图,在平面直角坐标系中,菱形ABCD的顶点A,C在x轴上,顶点B的坐标为(2,3),那么顶点D的坐标是 .
13.(5分)如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
14.(5分)小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球的个数约是 个.
三、解答题(本大题共3小题,每小题8分,共24分)
15.(8分)如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).
(1)将△ABC向右平移2个单位,作出△A'B'C';
(2)写出△A'B'C'的顶点坐标.
16.(8分)如图,已知△ABC中,AB=3,AC=5,∠BAE=∠CAE,BE⊥AE于点E,BE的延长线交AC于点D,F是BC的中点,求EF的长.
17.(8分)如图,在同一平面直角坐标系xOy中,A、B两点的坐标分别为A(3,0),B(2,2),直线y1=k1x+b经过A,B两点,且与直线y2=k2x交于点B.
(1)求这两条直线的函数表达式;
(2)根据图象直接写出当y1<y2时x的取值范围.
四、解答题(本大题共3个小题,每小题10分,共30分)
18.(10分)蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计,以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题:
组别
分组
频数
频率
1
50≤x<60
9
0.18
2
60≤x<70
m
b
3
70≤x<80
21
0.42
4
80≤x<90
a
0.06
5
90≤x<100
2
n
(1)根据上表填空:a= ,b= ,m= .
(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在90≤x≤100的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
19.(10分)一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
20.(10分)如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE交BC于点F,连接AC,BE;若∠AFC=2∠D,AB=2,BC=4.
(1)求证:四边形ABEC是矩形;
(2)求BE的长.
五、解答题(本题满分10分)
21.(10分)如图,在平面直角坐标系中,已知点A(﹣6,0),B(0,8),点C为OB的中点,点D在第二象限,四边形AOCD为矩形,直线AB交DC于点E.
(1)求直线AB的解析式及点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发沿线段AO以每秒2个单位长度的速度向终点O运动,当其中一点到达终点时,两点同时停止运动.连接NP,设点P的运动时间为t秒.
①当t为何值时,四边形ANPE为平行四边形?
②当t为何值时,四边形ANPD为矩形?
六、解答题(本题满分14分)
22.(14分)AC是菱形ABCD的对角线,∠B=60°,AB=2,∠EAF=60°,将∠EAF绕顶点A旋转,∠EAF的两边分别与直线BC,CD交于点E,F,连接EF.
(1)【感知】如图1,若E,F分别是边BC,CD的中点,则CE+CF= ;
(2)【探究】如图2,若E是线段BC上任意一点,求CE+CF的长;
(3)【应用】如图3,若E是BC延长线上一点,且EF⊥BC,求△AEF的周长.
2019-2020学年湖南省益阳市桃江县八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题5分,共40分;在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)
1.【答案】D
【解答】解:分两种情况:
①当3和4为两条直角边长时,
②当4为斜边长时,
综上所述:第三边长的平方是7或25.
故选:D.
2.【答案】B
【解答】解:A、∵AB=DE,BC=EF,∠A=∠D=90°,∴根据HL证明Rt△ABC≌Rt△DEF,不符合题意;
B、∵AB=DE,BC=EF,∠A=∠D=80°,根据ASS不能推出△ABC≌△DEF,故本选项符合题意;
C、∵AB=DE,∠A=∠D=90°,∠B=∠E=40°,∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;
D、∵BC=EF,∠A=∠D=80°,∠B=∠E=40°,∴利用AAS能推出△ABC≌△DEF,故本选项不符合题意;
故选:B.
3.【答案】D
【解答】解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
故选:D.
4.【答案】A
【解答】解:A、是中心对称图形,符合题意;
B、不是中心对称图形,不合题意;
C、是轴对称图形,不是中心对称图形,不合题意;
D、是轴对称图形,不是中心对称图形,不合题意.
故选:A.
5.【答案】C
【解答】解:点A(﹣3,5)向右平移4个单位长度,再向下平移2个单位长度可得点的坐标(1,2),
故选:C.
6.【答案】D
【解答】解:∵洗衣机工作前洗衣机内无水,
∴A,B两选项不正确,被淘汰;
∴C选项不正确,被淘汰,
故选:D.
7.【答案】A
【解答】解:在y=2x+1中,
当x=1时,代入得y=3,所以点(3,2)不在直线上,
当x=0时,代入得y=1,所以点(0,1)在直线上,
综上可知在直线y=8x+1上的点只有一个,
故选:A.
8.【答案】D
【解答】解:A.得分在70~80分的人数最多,此选项正确;
B.该班的总人数为4+12+14+8+2=40(人),此选项正确;
D.得分及格(≥60)的有12+14+2+2=36人,此选项错误;
故选:D.
二、填空题(本大题共6个小题,每小题5分,共30分;把答案填在题中的横线上)
9.【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2×2=4,
∴BC=AB=2,
故答案为:2.
10.【答案】见试题解答内容
【解答】解:
如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
若AE=CF,则有AO﹣AE=CO﹣CF,即OE=OF,
故答案为:AE=CF.
11.【答案】见试题解答内容
【解答】解:如图:
∴OA=OB=4,
∴OA?OB=OA?EF+OB?EG,
∴EF+EG=4.
故答案为:4.
12.【答案】见试题解答内容
【解答】解:∵菱形ABCD的顶点A,C在x轴上,
∴AC⊥BD,菱形ABCD关于x轴对称,
∵顶点B的坐标为(2,3),
故答案为:(2,﹣3).
13.【答案】见试题解答内容
【解答】解:∵直线y=ax+b和直线y=kx交点P的坐标为(1,2),
∴关于x,y的二元一次方程组的解为.
故答案为.
14.【答案】见试题解答内容
【解答】解:设黑球的个数为x,
∵黑球的频率在0.7附近波动,∴摸出黑球的概率为0.7,即=0.2,解得x=2100个.
三、解答题(本大题共3小题,每小题8分,共24分)
15.【答案】见试题解答内容
【解答】解:(1)如图,△A'B'C'即为所求.
(2)A′(2,2),B′(﹣1,1),C′(5,﹣2).
16.【答案】1.
【解答】解:在△AEB和△AED中,
,
∴AD=AB=3,BE=ED,
∵BE=ED,BF=FC,
∴EF=CD=1.
17.【答案】见试题解答内容
【解答】解:(1)∵直线y1=k1x+b经过A,B两点,A(3,0),B(4,2),
∴,解得,
∵直线y2=k2x经过点B.
解得k2=1,
∴这两条直线的函数表达式为y7=﹣2x+6和y2=x;
(2)由图象可知,当x>2时,y1<y5.
四、解答题(本大题共3个小题,每小题10分,共30分)
18.【答案】见试题解答内容
【解答】解:(1)9÷0.18=50(人).
a=50×0.06=4,m=50﹣(9+21+3+2)=15,b=15÷50=0.7.
(2)全班共有50名学生,中位数是第25、26个数据的平均数,第25、26个数据在第3组,
(7)×600=24(人).
答:共有24名学生被选拔参加决赛.
19.【答案】见试题解答内容
【解答】解:(1)设当4≤x≤12时的直线方程为:y=kx+b(k≠0).
∵图象过(6,20)、(12,30),
解得:,
(2)根据图象,每分钟进水20÷4=5升,
解得:m=.
故每分钟进水、出水各是5升、升.
20.【答案】见试题解答内容
【解答】(1)证明;∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠ABC=∠D,
∴AB=CE,
∴BC=2BF,AE=2AF,
∴∠ABC=∠BAE,
∴AE=BC,
(2)解:∵四边形ABEC是矩形,
∴BE===7.
五、解答题(本题满分10分)
21.【答案】见试题解答内容
【解答】解:(1)设直线AB的解析式为:y=kx+b,
将点A(﹣6,0),点B(0,8)代入y=kx+b得:,
∴直线AB的解析式为:y=x+8,
∴C(0,4),
∴CD∥OA,
将y=4代入y=x+8得:x=﹣3,
(2)①∵四边形AOCD为矩形,
∴当EP=AN时,四边形ANPE为平行四边形,
∴t=1,
②∵四边形AOCD为矩形,
∴当DP=AN时,四边形ANPD为矩形,
∴t=5,
∴当t=2s时,四边形ANPD为矩形.
六、解答题(本题满分14分)
22.【答案】见试题解答内容
【解答】解:(1)∵四边形ABCD是菱形,
∴BC=CD=AB=2,
∴CE=BC,CF=CD=1,
故答案为:2.
∴AB=BC,∠B+∠BCD=180°,
∴△ABC是等边三角形,∠ACB=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴△ABE≌△ACF(ASA),
∴CE+CF=CE+BE=BC=3;
∴AE=AF,CE=DF,
∴△AEF是等边三角形,
∵AB∥FC,∠FCE=∠B=60°,∠CEF=90°,
即CD+DF=2CE,CE=2,CF=4,
∴△AEF的周长为6.
同课章节目录
