青岛版九年级上册 数学 3.4 直线和圆的位置关系1课件(共21张PPT)
文档属性
| 名称 | 青岛版九年级上册 数学 3.4 直线和圆的位置关系1课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 12:39:15 | ||
图片预览






文档简介
(共21张PPT)
直线和圆的位置关系
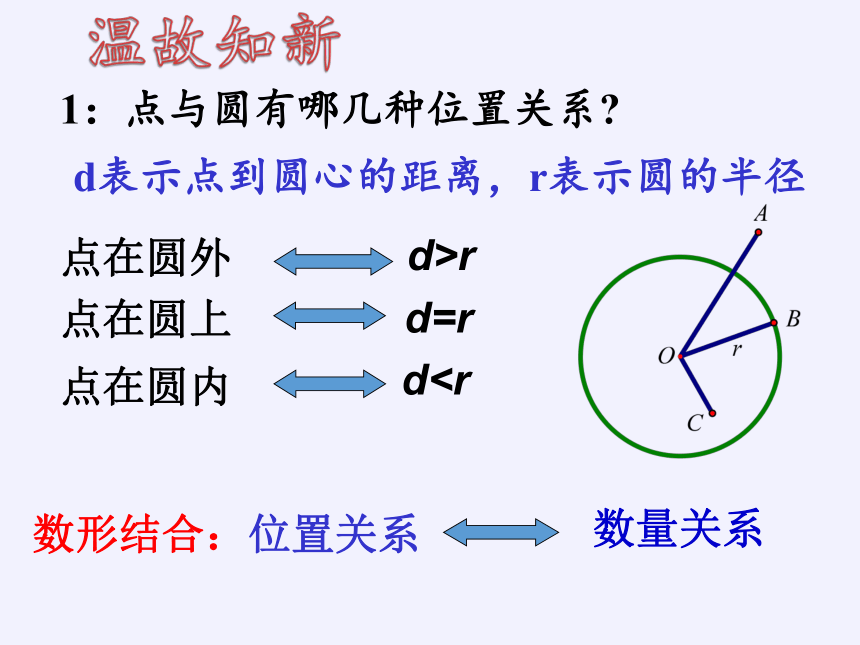
d>r
d=r
点在圆外
点在圆上
点在圆内
d1:点与圆有哪几种位置关系?
d表示点到圆心的距离,r表示圆的半径
数形结合:位置关系
数量关系
温故知新
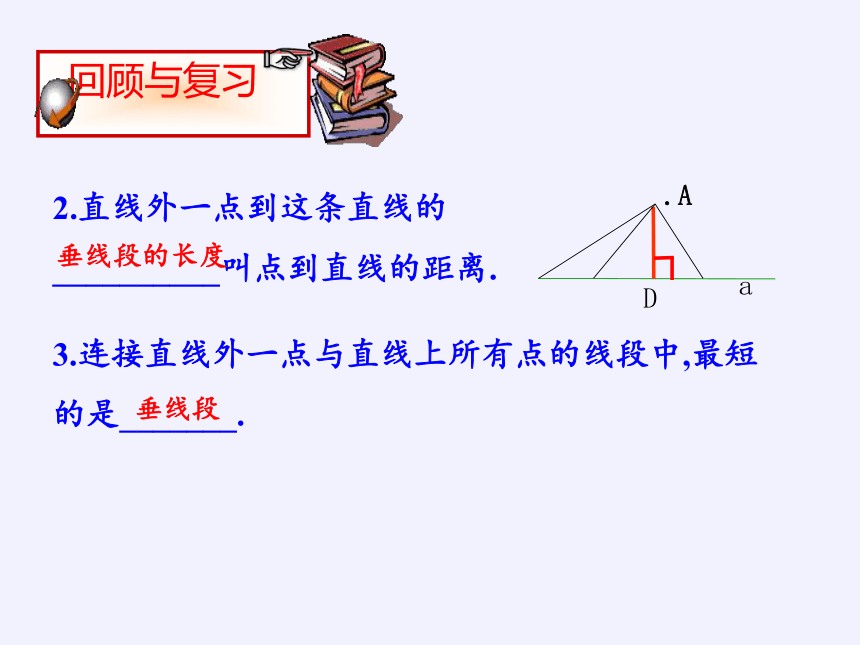
3.连接直线外一点与直线上所有点的线段中,最短
的是_______.
2.直线外一点到这条直线的__________叫点到直线的距离.
垂线段
a
.A
D
垂线段的长度
回顾与复习
?
观
察
“大漠孤烟直,长河落日圆”
是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆有几种位置关系?
1.了解直线与圆的位置关系;
2.会根据公共点的个数或圆心到直线的距离与圆的半径的关系判定直线与圆的位置关系;
3.感悟分类的数学思想.
学习目标
请根据你的观察,在纸上画出直线与圆的位置关系示意图。
动手操作:
自学课本91页-92页内容,并完成以下问题:
(1)直线和圆的公共点个数最少时有几个?最多时有几个?
(2)通过学习,归纳直线和圆的位置关系可分为几种类型?
自主先学
.O
特点:直线和圆没有公共点时,叫做直线和圆相离.
特点:直线和圆有唯一的公共点时,叫做直线和圆相切.这时的直线叫做圆的切线,
唯一的公共点叫做切点.
1.直线与圆的位置关系
.O
.A
.B
.O
.A
切点
归纳小结:
特点:直线和圆有两个公共点时,叫做
直线和圆相交,这时的直线叫做圆的割线.
(图形特征--用公共点的个数来区分)
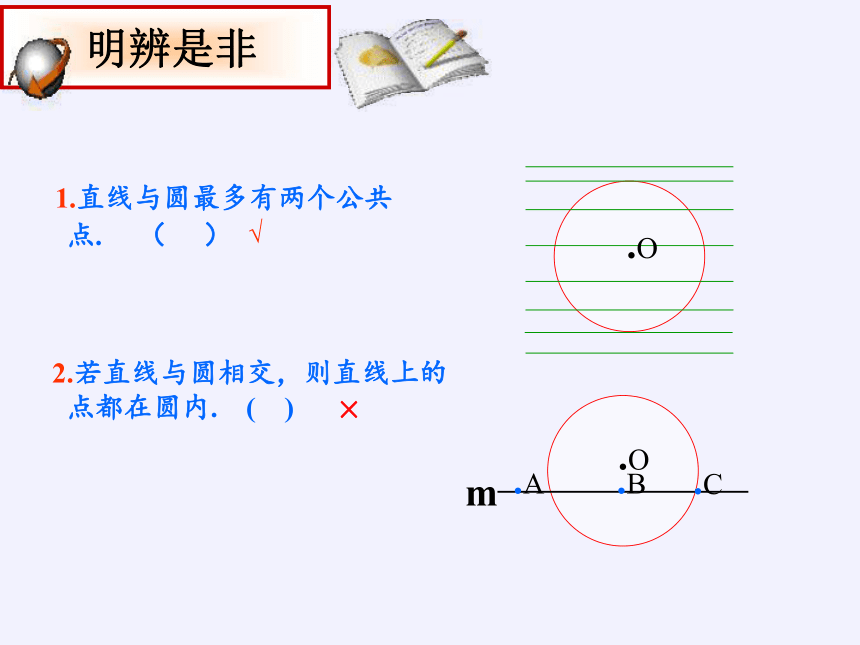
1.直线与圆最多有两个公共
点.
(
)
2.若直线与圆相交,则直线上的
点都在圆内.
(
)
√
×
.O
.A
.B
.C
.O
m
随堂
练习
1
1
随堂
练习
1
1
明辨是非
3.若A、B是⊙O外两点,
则直线AB
与⊙O相离。(
)
4.若C为⊙O内与O点不重合的一点,
则直线CO与⊙O相交。(
)
√
×
想一想?
若C为⊙O内的一点,A为任意一点,
则直线AC与⊙O一定相交。是否正确?
.C
随堂
练习
1
1
随堂
练习
1
1
明辨是非
直线与圆的位置关系(数量特征)
设⊙O的半径为r,圆心O到直线的距离为d.
直线和圆相交
d
r;
直线和圆相切
直线和圆相离
d
r;
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
d
r;
<
=
>
合作探究
1.已知圆的直径为13cm,设直线和圆心的距离为d
:
3)若d=
8
cm
,则直线与圆______,
直线与圆有____个公共点.
2)若d=6.5cm
,则直线与圆______,
直线与圆有____个公共点.
1)若d=4.5cm
,则直线与圆 ,
直线与圆有____个公共点.
3)若AB和⊙O相交,则
_________________.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据
条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
小试牛刀
d
<
5cm
0cm≤
2
1
0
例1
在Rt△ABC中,∠C=90°,BC=4cm
,AC=3cm,
以点C为圆心,r为半径画圆,当r分别取下列各值时,斜边AB所在的直线与⊙C具有怎样的位置关系?
(1)r=2cm
;
(2)r=2.4cm;
(3)r=3cm
.
B
C
A
D
【例题精讲】
解:过C作CD⊥AB,垂足为D
在Rt△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
所以
(1)当r=2cm时,
d>r,
直线AB与⊙C相离;
B
C
A
4
3
D
d
(2)当r=2.4cm时,
d=r,
直线AB与⊙C相切;
(3)当r=3cm时,
有d直线AB与⊙C相交;
B
C
A
4
3
D
B
C
A
4
3
D
d
d
应用扩展
1.已知⊙O的半径为5cm,点P在直线L上,若OP=5cm,
则直线L与⊙O有怎样的位置关系?画图说明.
2.已知等腰直角三角形的直角边长为2cm,以直角顶点为圆心,以r为半径画圆.当r在什么范围内取值时,所画的圆与斜边相交?
课堂小结:直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
1.⊙O的半径为3,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )A.d>3
B.d<3
C.d≤3
D.d=3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )A.相离
B.相交
C.相切
D.相切或相交
3.如图,已知∠BAC=300,M为AC上一点,且AM=5cm,以M为圆心、r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
达标检测
A层
M
A
B
C
D
A
C
相离
相交
相切
1.等边三角形ABC的边长为2,则以点A为圆心,半径为1.7的圆与直线BC的位置关系是
;以点A为圆心,
为半径的圆与直线BC相切.
2.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
达标检测
B层
相离
?
r=2时,相离;
r=4时,相交;
课后作业
1.必做:配套练习册39页1-4题
2.选做:课本99页1-2题
祝同学们学习进步!
谢
谢
直线和圆的位置关系
d>r
d=r
点在圆外
点在圆上
点在圆内
d
d表示点到圆心的距离,r表示圆的半径
数形结合:位置关系
数量关系
温故知新
3.连接直线外一点与直线上所有点的线段中,最短
的是_______.
2.直线外一点到这条直线的__________叫点到直线的距离.
垂线段
a
.A
D
垂线段的长度
回顾与复习
?
观
察
“大漠孤烟直,长河落日圆”
是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆有几种位置关系?
1.了解直线与圆的位置关系;
2.会根据公共点的个数或圆心到直线的距离与圆的半径的关系判定直线与圆的位置关系;
3.感悟分类的数学思想.
学习目标
请根据你的观察,在纸上画出直线与圆的位置关系示意图。
动手操作:
自学课本91页-92页内容,并完成以下问题:
(1)直线和圆的公共点个数最少时有几个?最多时有几个?
(2)通过学习,归纳直线和圆的位置关系可分为几种类型?
自主先学
.O
特点:直线和圆没有公共点时,叫做直线和圆相离.
特点:直线和圆有唯一的公共点时,叫做直线和圆相切.这时的直线叫做圆的切线,
唯一的公共点叫做切点.
1.直线与圆的位置关系
.O
.A
.B
.O
.A
切点
归纳小结:
特点:直线和圆有两个公共点时,叫做
直线和圆相交,这时的直线叫做圆的割线.
(图形特征--用公共点的个数来区分)
1.直线与圆最多有两个公共
点.
(
)
2.若直线与圆相交,则直线上的
点都在圆内.
(
)
√
×
.O
.A
.B
.C
.O
m
随堂
练习
1
1
随堂
练习
1
1
明辨是非
3.若A、B是⊙O外两点,
则直线AB
与⊙O相离。(
)
4.若C为⊙O内与O点不重合的一点,
则直线CO与⊙O相交。(
)
√
×
想一想?
若C为⊙O内的一点,A为任意一点,
则直线AC与⊙O一定相交。是否正确?
.C
随堂
练习
1
1
随堂
练习
1
1
明辨是非
直线与圆的位置关系(数量特征)
设⊙O的半径为r,圆心O到直线的距离为d.
直线和圆相交
d
r;
直线和圆相切
直线和圆相离
d
r;
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
d
r;
<
=
>
合作探究
1.已知圆的直径为13cm,设直线和圆心的距离为d
:
3)若d=
8
cm
,则直线与圆______,
直线与圆有____个公共点.
2)若d=6.5cm
,则直线与圆______,
直线与圆有____个公共点.
1)若d=4.5cm
,则直线与圆 ,
直线与圆有____个公共点.
3)若AB和⊙O相交,则
_________________.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据
条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
小试牛刀
d
<
5cm
0cm≤
2
1
0
例1
在Rt△ABC中,∠C=90°,BC=4cm
,AC=3cm,
以点C为圆心,r为半径画圆,当r分别取下列各值时,斜边AB所在的直线与⊙C具有怎样的位置关系?
(1)r=2cm
;
(2)r=2.4cm;
(3)r=3cm
.
B
C
A
D
【例题精讲】
解:过C作CD⊥AB,垂足为D
在Rt△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
所以
(1)当r=2cm时,
d>r,
直线AB与⊙C相离;
B
C
A
4
3
D
d
(2)当r=2.4cm时,
d=r,
直线AB与⊙C相切;
(3)当r=3cm时,
有d
B
C
A
4
3
D
B
C
A
4
3
D
d
d
应用扩展
1.已知⊙O的半径为5cm,点P在直线L上,若OP=5cm,
则直线L与⊙O有怎样的位置关系?画图说明.
2.已知等腰直角三角形的直角边长为2cm,以直角顶点为圆心,以r为半径画圆.当r在什么范围内取值时,所画的圆与斜边相交?
课堂小结:直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
1.⊙O的半径为3,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )A.d>3
B.d<3
C.d≤3
D.d=3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )A.相离
B.相交
C.相切
D.相切或相交
3.如图,已知∠BAC=300,M为AC上一点,且AM=5cm,以M为圆心、r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
达标检测
A层
M
A
B
C
D
A
C
相离
相交
相切
1.等边三角形ABC的边长为2,则以点A为圆心,半径为1.7的圆与直线BC的位置关系是
;以点A为圆心,
为半径的圆与直线BC相切.
2.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
达标检测
B层
相离
?
r=2时,相离;
r=4时,相交;
课后作业
1.必做:配套练习册39页1-4题
2.选做:课本99页1-2题
祝同学们学习进步!
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
