青岛版九年级上册 数学 2.1 锐角三角比课件(共21张PPT)
文档属性
| 名称 | 青岛版九年级上册 数学 2.1 锐角三角比课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 12:39:00 | ||
图片预览






文档简介
(共21张PPT)
2.1
锐角三角比
学习目标
【教学目标】:
1、通过观察、探究、交流、猜想等数学活动,探索锐角三角比的概念.
2、能叙述锐角三角比的概念,记住三角比的符号,掌握锐角三角比的表示方法.
3、会求直角三角形中指定锐角的三角比.
【重、难点】:
重点:探索锐角三角比的意义.
难点:求直角三角形中指定锐角的三角比.
小小设计师
上图为一社区幼儿园的滑梯,为
了确保小朋友在玩耍过程中能更
加安全你能否用你学过的知识
利用钢管为小朋友们将这个滑梯
变得更加牢固呢?
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
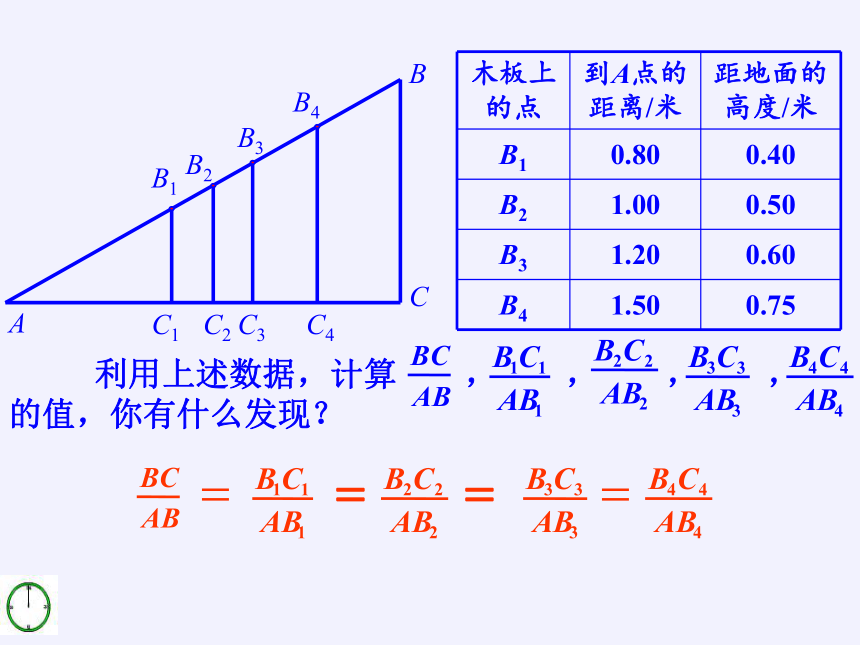
小亮借助工具测得滑梯的长度AB为4.00米,高度为2.00米(如图),在AB上分别取了四点,量得点B1,B2,B3,B4到A点的距离AB1,AB2,AB3,AB4与它们距地面的高度B1C1,B2C2,B3C3,B4C4,数据如下表所示:
木板上
的点
到A点的
距离/米
距地面的
高度/米
B1
0.80
0.40
B2
1.00
0.50
B3
1.20
0.60
B4
1.50
0.75
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
木板上
的点
到A点的
距离/米
距地面的
高度/米
B1
0.80
0.40
B2
1.00
0.50
B3
1.20
0.60
B4
1.50
0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
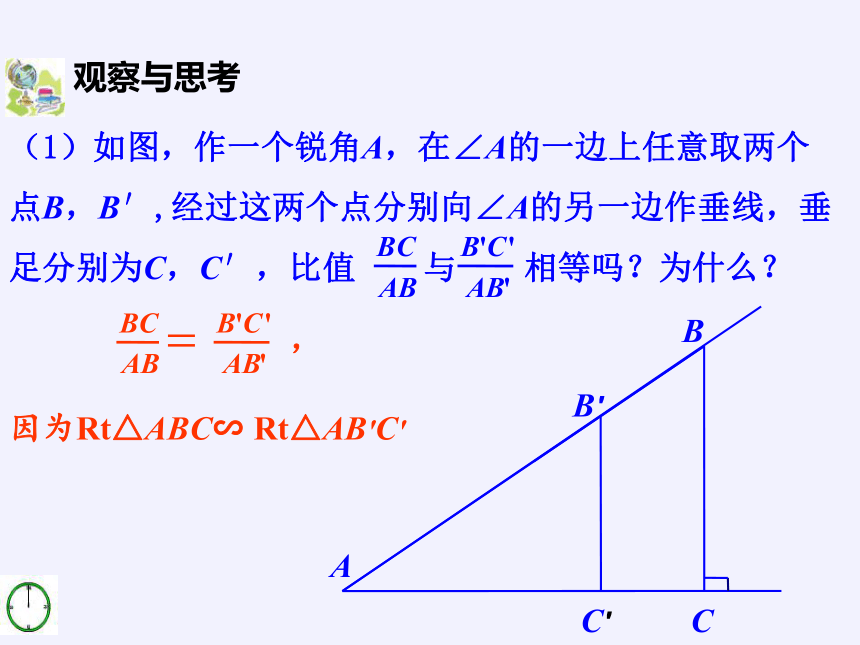
因为Rt△ABC∽
Rt△AB′C′
A
B
C
B′
C′
观察与思考
(1)如图,作一个锐角A,在∠A的一边上任意取两个点B,B′,经过这两个点分别向∠A的另一边作垂线,垂足分别为C,C′,比值 与 相等吗?为什么?
AB
BC
'
'
'
AB
C
B
,
'
'
'
AB
C
B
AB
BC
=
A
B
C
B′
C′
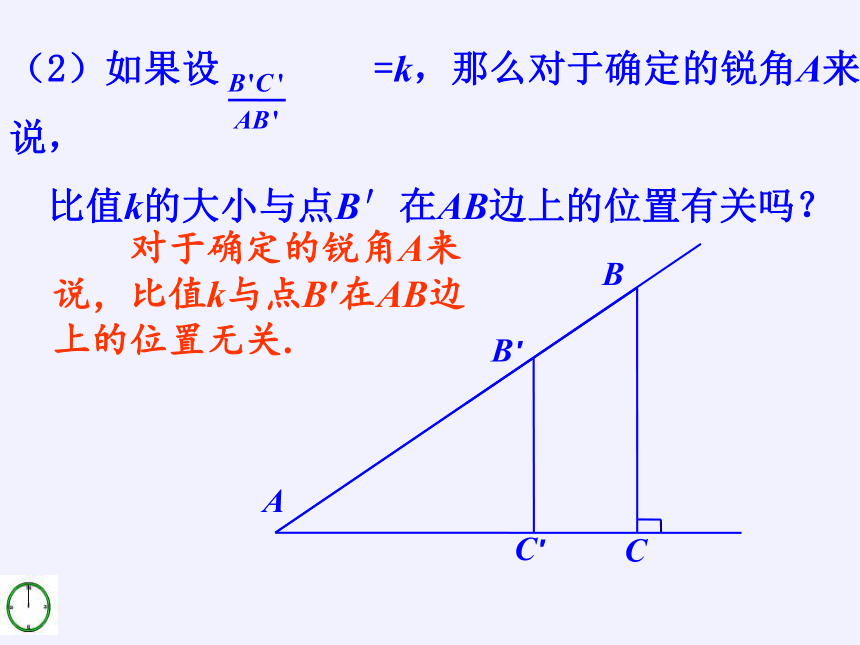
对于确定的锐角A来说,比值k与点B′在AB边上的位置无关.
(2)如果设
=k,那么对于确定的锐角A来说,
比值k的大小与点B′在AB边上的位置有关吗?
'
'
'
AB
C
B
A
B
C
B′
C′
B″
C″
对于确定的锐角A来说,比值k与点B′在AB边上的位置无关,只与锐角A的大小有关.
(3)如图,以点A为端点,在锐角A的内部作一条射线,在这条射线上取点B″,使AB
″=
AB′,这样又得到了一个锐角∠CAB″.过B
″作
B″C″⊥AC,垂足为C
″,比
与k的值相等吗?为什么?由此你得到怎样的结论?
"
"
"
AB
C
B
温故知新:
Rt△ABC
中,斜边是(
),∠A的对边是
(
),
∠A
的邻边是(
).
A
B
C
A
B
C
斜边
∠A的邻边
∠A的对边
由锐角A确定的比
叫做∠A的正弦,
∠A的对边
斜边
sinA
=
∠A的对边
斜边
记作sinA,即
由锐角A确定的比
叫做∠A的余弦,
∠A的邻边
斜边
cosA
=
∠A的邻边
斜边
记作cosA,即
∠A的对边
∠A的邻边
由锐角A确定的比
叫做∠A的正切,
记作tanA,即
tanA
=
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
一个锐角A的三角比只与它的大小有关.
注:1.sinA,cosA,tanA分别是一个完整的记号.记
号里习惯省去角的符号“∠”,不能理解成
sin·A,cos·A,tan·A.
A
B
C
2.在Rt△ABC中,通常,把∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c.
如图,你能用a、b、c表示∠A的正弦、余弦和正切吗?
c
a
b
sinA=
c
a
cosA=
c
b
tanA=
b
a
特别,sinA
不是一个角,是一个比值,没有单位.
牛刀小试:
A
10m
6m
B
C
(1)
如图
tanA=
m
(2)如图,锐角△ABC中,tanA=
×
×
注意:锐角三角比没有单位;锐角三角比在直角三角形中求解.
牛刀小试
(3)如果一个直角三角形各边都扩大2倍,则锐角的正弦值也扩大
2倍
.
x
注意:锐角三角比与直角三角形的大小没关系,与角的大小有关系.
例题讲解
例:如图,在Rt△ABC中,∠C=90°,a=2,b=4,
求∠A的正弦、余弦、正切的值.
B
A
C
解:在Rt△ABC中,∠C=90°
因为a=2,b=4,所以
4
2
5
2
c=
.
b
a
5
2
2
4
2
2
2
2
=
+
=
+
sinA=
5
5
5
2
2
=
=
c
a
cosA=
5
5
2
5
2
4
=
=
c
b
tanA=
2
1
4
2
=
=
b
a
1.如果R
t△ABC∽
R
t△A′B′C′,∠C=
∠C′=90°,sinA等于sinA′吗?为什么?
cosA与cosA′呢?
2.如图,在R
t△ABC中,
∠C=90°,
c=3,a=2,求∠A的正弦、余弦、正切的值.
sinA=sinA′,
cosA=cosA′,
因为R
t△ABC∽
R
t△A′B′C′,∠A=
∠A′.
tanA=
5
5
2
cosA=
3
5
sinA=
3
2
对应练习
B
A
C
对应练习
3、求出如图所示的Rt△ABC的sinA和sinB、tanA和cosB的值.
A
C
B
⑵
5
13
A
C
B
⑴
4
3
1.
∠
A的正弦:
sinA
=
∠A的对边
斜边
∠A的余弦:
cosA
=
∠A的邻边
斜边
∠A的正切:
tanA
=
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
2.一个锐角的三角比只与它的大小有关.
课堂小结
作业
必做题:课本P41
1、2、3题
选做题:课本P41
4、5、6题
谢
谢
2.1
锐角三角比
学习目标
【教学目标】:
1、通过观察、探究、交流、猜想等数学活动,探索锐角三角比的概念.
2、能叙述锐角三角比的概念,记住三角比的符号,掌握锐角三角比的表示方法.
3、会求直角三角形中指定锐角的三角比.
【重、难点】:
重点:探索锐角三角比的意义.
难点:求直角三角形中指定锐角的三角比.
小小设计师
上图为一社区幼儿园的滑梯,为
了确保小朋友在玩耍过程中能更
加安全你能否用你学过的知识
利用钢管为小朋友们将这个滑梯
变得更加牢固呢?
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
小亮借助工具测得滑梯的长度AB为4.00米,高度为2.00米(如图),在AB上分别取了四点,量得点B1,B2,B3,B4到A点的距离AB1,AB2,AB3,AB4与它们距地面的高度B1C1,B2C2,B3C3,B4C4,数据如下表所示:
木板上
的点
到A点的
距离/米
距地面的
高度/米
B1
0.80
0.40
B2
1.00
0.50
B3
1.20
0.60
B4
1.50
0.75
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
木板上
的点
到A点的
距离/米
距地面的
高度/米
B1
0.80
0.40
B2
1.00
0.50
B3
1.20
0.60
B4
1.50
0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
因为Rt△ABC∽
Rt△AB′C′
A
B
C
B′
C′
观察与思考
(1)如图,作一个锐角A,在∠A的一边上任意取两个点B,B′,经过这两个点分别向∠A的另一边作垂线,垂足分别为C,C′,比值 与 相等吗?为什么?
AB
BC
'
'
'
AB
C
B
,
'
'
'
AB
C
B
AB
BC
=
A
B
C
B′
C′
对于确定的锐角A来说,比值k与点B′在AB边上的位置无关.
(2)如果设
=k,那么对于确定的锐角A来说,
比值k的大小与点B′在AB边上的位置有关吗?
'
'
'
AB
C
B
A
B
C
B′
C′
B″
C″
对于确定的锐角A来说,比值k与点B′在AB边上的位置无关,只与锐角A的大小有关.
(3)如图,以点A为端点,在锐角A的内部作一条射线,在这条射线上取点B″,使AB
″=
AB′,这样又得到了一个锐角∠CAB″.过B
″作
B″C″⊥AC,垂足为C
″,比
与k的值相等吗?为什么?由此你得到怎样的结论?
"
"
"
AB
C
B
温故知新:
Rt△ABC
中,斜边是(
),∠A的对边是
(
),
∠A
的邻边是(
).
A
B
C
A
B
C
斜边
∠A的邻边
∠A的对边
由锐角A确定的比
叫做∠A的正弦,
∠A的对边
斜边
sinA
=
∠A的对边
斜边
记作sinA,即
由锐角A确定的比
叫做∠A的余弦,
∠A的邻边
斜边
cosA
=
∠A的邻边
斜边
记作cosA,即
∠A的对边
∠A的邻边
由锐角A确定的比
叫做∠A的正切,
记作tanA,即
tanA
=
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
一个锐角A的三角比只与它的大小有关.
注:1.sinA,cosA,tanA分别是一个完整的记号.记
号里习惯省去角的符号“∠”,不能理解成
sin·A,cos·A,tan·A.
A
B
C
2.在Rt△ABC中,通常,把∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c.
如图,你能用a、b、c表示∠A的正弦、余弦和正切吗?
c
a
b
sinA=
c
a
cosA=
c
b
tanA=
b
a
特别,sinA
不是一个角,是一个比值,没有单位.
牛刀小试:
A
10m
6m
B
C
(1)
如图
tanA=
m
(2)如图,锐角△ABC中,tanA=
×
×
注意:锐角三角比没有单位;锐角三角比在直角三角形中求解.
牛刀小试
(3)如果一个直角三角形各边都扩大2倍,则锐角的正弦值也扩大
2倍
.
x
注意:锐角三角比与直角三角形的大小没关系,与角的大小有关系.
例题讲解
例:如图,在Rt△ABC中,∠C=90°,a=2,b=4,
求∠A的正弦、余弦、正切的值.
B
A
C
解:在Rt△ABC中,∠C=90°
因为a=2,b=4,所以
4
2
5
2
c=
.
b
a
5
2
2
4
2
2
2
2
=
+
=
+
sinA=
5
5
5
2
2
=
=
c
a
cosA=
5
5
2
5
2
4
=
=
c
b
tanA=
2
1
4
2
=
=
b
a
1.如果R
t△ABC∽
R
t△A′B′C′,∠C=
∠C′=90°,sinA等于sinA′吗?为什么?
cosA与cosA′呢?
2.如图,在R
t△ABC中,
∠C=90°,
c=3,a=2,求∠A的正弦、余弦、正切的值.
sinA=sinA′,
cosA=cosA′,
因为R
t△ABC∽
R
t△A′B′C′,∠A=
∠A′.
tanA=
5
5
2
cosA=
3
5
sinA=
3
2
对应练习
B
A
C
对应练习
3、求出如图所示的Rt△ABC的sinA和sinB、tanA和cosB的值.
A
C
B
⑵
5
13
A
C
B
⑴
4
3
1.
∠
A的正弦:
sinA
=
∠A的对边
斜边
∠A的余弦:
cosA
=
∠A的邻边
斜边
∠A的正切:
tanA
=
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
2.一个锐角的三角比只与它的大小有关.
课堂小结
作业
必做题:课本P41
1、2、3题
选做题:课本P41
4、5、6题
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
