青岛版九年级上册 数学 1.3 相似三角形的性质课件(共26张PPT)
文档属性
| 名称 | 青岛版九年级上册 数学 1.3 相似三角形的性质课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.3
相似三角形的性质
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平
分线的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
1.回忆全等三角形的性质:
两个全等三角形具有哪些性质?
往事新忆
全等三角形的
①对应角相等
②对应边相等
③对应高相等
④对应中线相等
⑤对应角平分线相等
新知猜想
展开想象的翅膀:
相似三角形的对应角、对应边、
对应高、对应中线及对应角平分线
有何关系?
相似三角形的性质
根据相似三角形的定义我们可以知道哪些性质?
对应角相等,对应边成比例。
J我们把相似三角形对应边的比值称为相似比
猜想EQ相似三角形对应高的比是否等于相似比
信不信不由你
已知:如图,△ABC∽
△A′B′C′,
△ABC与
△A′B′C′的相似比是k,AD、A′D′是对应高。
求证:
B’
A’
C’
D’
A
B
C
D
证明:
∵△ABC∽△A
′
B
′
C
′
∴∠B=
∠B
′
∵
AD、A′D′分别是△ABC与
△A′B′C′的高
∴∠ADB=∠A′D′B′=90O
∴
△ABD∽△A
′
B
′
D
′
我也做一做:
相信自己,走向成功
A组,求证:相似三角形对应中线的比等于相似比。
B组,求证:相似三角形对应角平分线的比等于相似比
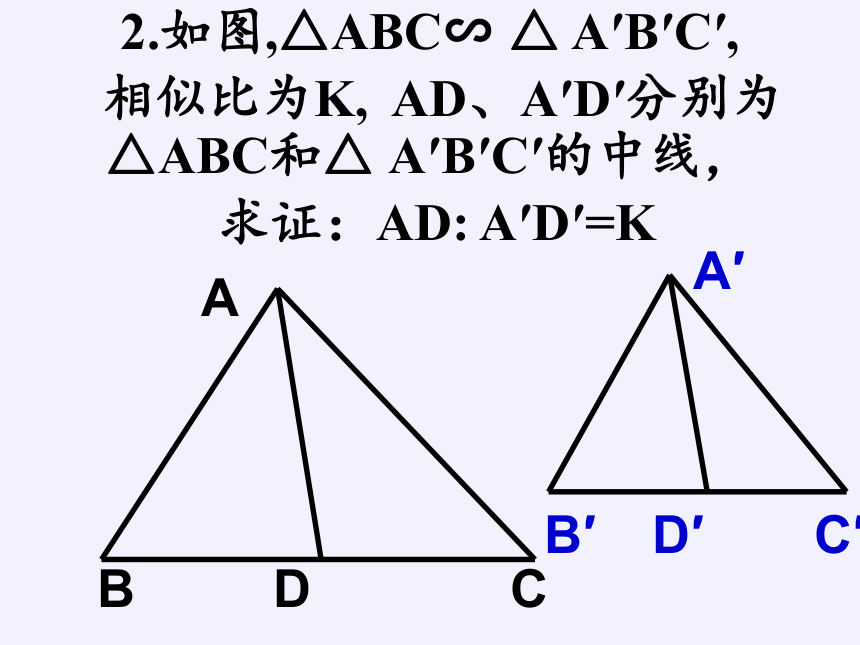
2.如图,△ABC∽
△
A′B′C′,
相似比为K,
AD、A′D′分别为
△ABC和△
A′B′C′的中线,
求证:AD:
A′D′=K
C′
A
B
C
D
A′
B′
D′
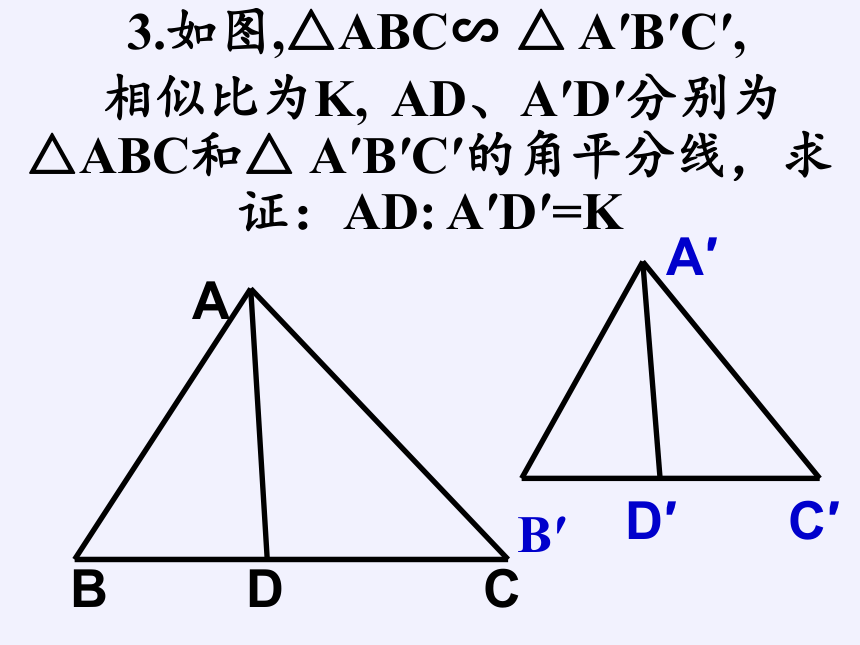
3.如图,△ABC∽
△
A′B′C′,
相似比为K,
AD、A′D′分别为
△ABC和△
A′B′C′的角平分线,求证:AD:
A′D′=K
A
B
C
D
B′
A′
C′
D′
相似三角形周长的比等于相似比吗?
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
做一做
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=(
)
⑵与⑴的面积比=(
)
⑶与⑴的相似比=(
)
⑶与⑴的面积比=(
)
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
∽
△
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
结论3
相似三角形的面积比为相似比的平方。
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
等于相似比.
面积的比等于相似比的平方
感悟与反思:相似三角形的性质
如图,四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们面积的比是多少?
相似多边形面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
延伸探究:
同样我们可以得出:相似多边形的周长比等于相似比
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为2:5,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
2:5
2:5
4:25
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4
:
3
4
:
3
2:5
小试牛刀
1.如图,在△ABC中,AD:DB=1:2,DE∥BC,若△ABC的面积为9,则S四边形DBCE=(
)
A
B
C
D
E
大显身手:
2.如图,在
ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,则S△EFB=(
)
D
A
B
C
E
F
3.已知:梯形ABCD中,AD∥BC,AD=36,BC=60cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
A
B
C
D
E
F
O
小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。
挑战自我
A
B
C
S
R
E
P
D
Q
(1)
△
ASR与△
ABC相似吗?为什么?
(2)求正方形SPQR的面积。
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的面积.
分析:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
例
题
解
析
A
B
C
S
R
E
P
D
Q
40
60
(1)如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。
P
B
A
C
D
E
F
M
N
如图,△ABC是一
块余料,边AB=90厘米,高CN=60厘米,要把它加工成正方形零件,使正方形
的一边在AB上,其余两个顶点分别在BC、AC上
(2)当DE是DP的1.5倍时恰好符合要求,求此时零件的面积是多少?
(3)在问题(2)中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)
变式训练:
自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是
,周长比是
,面积比是
.
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为
cm.
3、如果把一个三角形每条边的长都扩大为原来
的5倍,那么它的周长扩大为原来的
倍,
而面积扩大为原来的
倍。
4、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为(
)
(A)1:2
(B)1:3
(C)1;4
(D)1:5
A
B
C
D
E
知识象一艘船
让它载着我们
驶向理想的
……
你今天努力了吗?
小结
这节课你有什么收获呢
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
谢
谢
1.3
相似三角形的性质
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平
分线的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
1.回忆全等三角形的性质:
两个全等三角形具有哪些性质?
往事新忆
全等三角形的
①对应角相等
②对应边相等
③对应高相等
④对应中线相等
⑤对应角平分线相等
新知猜想
展开想象的翅膀:
相似三角形的对应角、对应边、
对应高、对应中线及对应角平分线
有何关系?
相似三角形的性质
根据相似三角形的定义我们可以知道哪些性质?
对应角相等,对应边成比例。
J我们把相似三角形对应边的比值称为相似比
猜想EQ相似三角形对应高的比是否等于相似比
信不信不由你
已知:如图,△ABC∽
△A′B′C′,
△ABC与
△A′B′C′的相似比是k,AD、A′D′是对应高。
求证:
B’
A’
C’
D’
A
B
C
D
证明:
∵△ABC∽△A
′
B
′
C
′
∴∠B=
∠B
′
∵
AD、A′D′分别是△ABC与
△A′B′C′的高
∴∠ADB=∠A′D′B′=90O
∴
△ABD∽△A
′
B
′
D
′
我也做一做:
相信自己,走向成功
A组,求证:相似三角形对应中线的比等于相似比。
B组,求证:相似三角形对应角平分线的比等于相似比
2.如图,△ABC∽
△
A′B′C′,
相似比为K,
AD、A′D′分别为
△ABC和△
A′B′C′的中线,
求证:AD:
A′D′=K
C′
A
B
C
D
A′
B′
D′
3.如图,△ABC∽
△
A′B′C′,
相似比为K,
AD、A′D′分别为
△ABC和△
A′B′C′的角平分线,求证:AD:
A′D′=K
A
B
C
D
B′
A′
C′
D′
相似三角形周长的比等于相似比吗?
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
做一做
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=(
)
⑵与⑴的面积比=(
)
⑶与⑴的相似比=(
)
⑶与⑴的面积比=(
)
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
∽
△
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
结论3
相似三角形的面积比为相似比的平方。
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
等于相似比.
面积的比等于相似比的平方
感悟与反思:相似三角形的性质
如图,四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们面积的比是多少?
相似多边形面积比等于相似比的平方.
A
B
C
A′
B′
C′
D
D′
延伸探究:
同样我们可以得出:相似多边形的周长比等于相似比
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为2:5,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
2:5
2:5
4:25
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4
:
3
4
:
3
2:5
小试牛刀
1.如图,在△ABC中,AD:DB=1:2,DE∥BC,若△ABC的面积为9,则S四边形DBCE=(
)
A
B
C
D
E
大显身手:
2.如图,在
ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,则S△EFB=(
)
D
A
B
C
E
F
3.已知:梯形ABCD中,AD∥BC,AD=36,BC=60cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
A
B
C
D
E
F
O
小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。
挑战自我
A
B
C
S
R
E
P
D
Q
(1)
△
ASR与△
ABC相似吗?为什么?
(2)求正方形SPQR的面积。
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的面积.
分析:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
例
题
解
析
A
B
C
S
R
E
P
D
Q
40
60
(1)如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。
P
B
A
C
D
E
F
M
N
如图,△ABC是一
块余料,边AB=90厘米,高CN=60厘米,要把它加工成正方形零件,使正方形
的一边在AB上,其余两个顶点分别在BC、AC上
(2)当DE是DP的1.5倍时恰好符合要求,求此时零件的面积是多少?
(3)在问题(2)中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)
变式训练:
自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是
,周长比是
,面积比是
.
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为
cm.
3、如果把一个三角形每条边的长都扩大为原来
的5倍,那么它的周长扩大为原来的
倍,
而面积扩大为原来的
倍。
4、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为(
)
(A)1:2
(B)1:3
(C)1;4
(D)1:5
A
B
C
D
E
知识象一艘船
让它载着我们
驶向理想的
……
你今天努力了吗?
小结
这节课你有什么收获呢
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
