2011-2012学年七年级数学(人教版上)同步练习第四章第三节 角(二)角的度量与画法
文档属性
| 名称 | 2011-2012学年七年级数学(人教版上)同步练习第四章第三节 角(二)角的度量与画法 |
|
|
| 格式 | zip | ||
| 文件大小 | 101.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-30 00:00:00 | ||
图片预览


文档简介
2011-2012学年七年级数学(人教版上)同步练习第四章
第三节 角(二)角的度量与画法
一. 教学内容:
角的度量与画法
【知识点讲解】
1. 角的度量:按对线、对中、度数的步骤用量角器量出角的度数
2. 角的度数计算:角的单位是度分秒,都是60进制,可以比照时间中的时分秒理解,分别用“°”、“ ’”、“ ””来表示。
3. 余角、补角的概念与性质:如果两个角的和是90度(或直角)时,叫做两个角互余;
4. 如果两个角的和是180度(或平角)时,叫做两个角互补。
(补角同理)
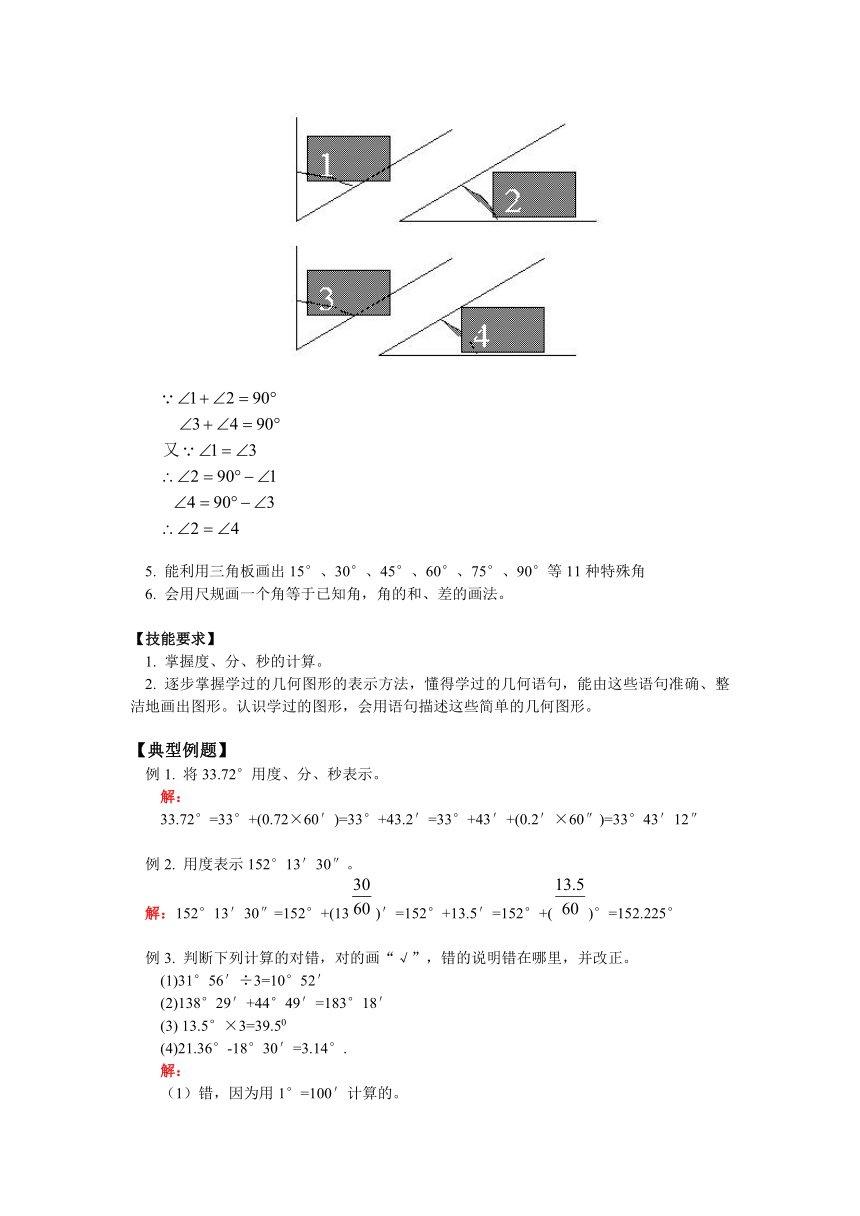
性质:同角(或等角)的余角相等;同角(或等角)的补角相等
(补角同理)
5. 能利用三角板画出15°、30°、45°、60°、75°、90°等11种特殊角
6. 会用尺规画一个角等于已知角,角的和、差的画法。
【技能要求】
1. 掌握度、分、秒的计算。
2. 逐步掌握学过的几何图形的表示方法,懂得学过的几何语句,能由这些语句准确、整洁地画出图形。认识学过的图形,会用语句描述这些简单的几何图形。
【典型例题】
例1. 将33.72°用度、分、秒表示。
解:
33.72°=33°+(0.72×60′)=33°+43.2′=33°+43′+(0.2′×60″)=33°43′12″
例2. 用度表示152°13′30″。
解:152°13′30″=152°+(13)′=152°+13.5′=152°+()°=152.225°
例3. 判断下列计算的对错,对的画“√”,错的说明错在哪里,并改正。
(1)31°56′÷3=10°52′
(2)138°29′+44°49′=183°18′
(3) 13.5°×3=39.50
(4)21.36°-18°30′=3.14°.
解:
(1)错,因为用1°=100′计算的。
应改为:31°56′÷3=(30°+114′+120″) ÷3=10°38′40″
(2)(√)。
(3)错,本题是十进制小数,要按一般乘法规则进位,应改为13.5°×3=40.5°。
(4)错,因为被减数与减数单位不同,不能相减。
应改为:21.36°-18°30′=21°+0.36×60′-18°30’ =21°21′+0.6×60″-18°30′=21°21′36″-18°30′=20°81′36″-18°30′=2°51′36″
例4. 已知∠α=22.68°,∠β=18°41′55″,求∠α与∠β的差(结果用度、分、秒表示)
分析:因为结果要求用度、分、秒表示,所以,先将∠α表示为度分秒的形式:
22.68°=22°+0.68°=22°+0.68×60’=22°+40.8’=22°+40’+0.8×60″=22°+40’+48″=22°40’48’’;然后求∠α-∠β=22°40’48’’-18°41’55’’(1)=21°99’108″-18°41’55’’(2)=3°58’53″(3)
注意:两角度相加减时,“度”与“度”、“分”与“分”、“秒”与“秒”分别相加减,如第(3)步;当被减数中的“秒”不够减时(如第(1)步),可从40′中借来1’,化作60″,22°40′48″就变为22°39′108″;当被减数中的“分”不够减时(如第(2)步),可从22°借1°,化作60′,这时,22°39′108″就变为21°99′108″。
例5. 求24°35′43″与121°48′56″的和(结果精确到分)
解:24°35′43″+121°48′56″=145°83′99″ (1)=145°84′39″ (2) =146°24′39″ (3) ≈146°25′ (4)
注意:
①本题可直接求得两角之和为145°83′99″,但是99″要变成1′39″(如第(2)步),84′要变成1°24′(如第(3)步)。
②精确到分时,将不足30″的舍去,30″及超过30″的进为1′;精确到度时,则将不足30′的舍去,30′及超过30′的进为1°。③由低级单位向高级单位转化或由高级单位向低级单位转化,要逐级进行,千万不要“越级”。
例6. 把1个周角7等分,求每份角的度数。(精确到分)
分析:1个周角为360°,那么把它7等分,每份角的度数可由360°÷7计算得出。
解:360°÷7=51°+3°÷7 =51°+180′÷7 ≈51°+26′=51°26′
注意:对分的十进制小数来说,仍按四舍五入方法进行近似计算。如25.7′≈26′,
8.4′≈8′。
例7.一个角比它的余角的多14°,求这个角的补角。
解:设这个角的度数为x°,则它的余角为(90-x) °,补角为(180-x) °,
由题意可得,x- (90-x)=14, 解方程得x=33,∴ 180-x=180-33=147°.
答:这个角的补角为147°。
例8.一个角是另一个角的3倍,且小角的余角与大角的补角之差为20°,求这两个角的度数。
解:设大角的度数为x, 则它的补角为(180-x) °,设小角为y°, 则它的余角为(90-y) °,
由题意可得
解方程组得
答:小角为55°,大角为165°。
说明:因为互余两角与互补两角之间的关系是数量关系,所以解这类计算题时,常用代数中的列方程解应用题的方法来做是很好的方法。
例9. 下午2点到2点30分,时钟的时针和分针各转过了多少度?
分析:时钟被分成12个大格时,相当于把圆周12等分,每一等份等于30°,分针转360°时,时针转一大格即30°。
解:时针是0. 5°×30=15°,分针是6°×30=180°
答:时针转了15°,分针转了180°。
例10. 在时刻8:25,时钟上的时针和分针之间的夹角是多少度?
分析:时针偏离0.5°×25=12.5°,分针6°×25=150°,8点时时针在分针前,30°×8=240°,240°—150°=90°,夹角为90°+12.5°=102.5°
例11. 已知OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1、∠3、∠4的度数。
解:∵OB是平分线
∴∠1=∠2
∵设一份角为x
∴∠2=∠1=x,∠3=3x,∠4=4x
∴x=40
∴∠1=40°,∠3=120°,∠4=160°
【模拟试题】(答题时间:30分钟)
1. 把30°23’45’’化成度;求46.83°化成度分秒,求109°11’4’’÷7
2. 一个角的补角是它的余角的4倍,求这个角的补角
3. 已知AOC为一直线,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,
∠DOE=72°,求∠EOC的度数。
4. 计算
5. 求时钟表面3点25分时,时针与分针的夹角是多少度?
6. 直线AB与CD相交于点O,OE平分∠AOC,∠BOC-∠BOD=20°,求∠BOE的度数。
7. 用三角板画出165°角
8. 甲乙两名学生在操场上,从同一旗杆处出发,甲向北走18米,乙向东走16米,以后又向北走6米,用1厘米代表2米,画出方位图,测量并计算甲乙的距离。
【试题答案】
1. 答30°23’45’’=:46.83°= 2. 设这个角的补角是X,根据题意得;X=4[90-(180-X)],解得;X=120;所以,这个角的补角是120°。
3.解法1 设∠AOB=x°,∠BOC=y°,则
解法2.设角EOC=2X,则角BOE=X, 角AOD=72°-X, 得方程;2(72°-X)+3X=180° 解得;X=36°,所以,角EOC=72度。
4. 5.时针每分钟转的角度是360°/(12*60)=1/2度,分针每分钟转360°/60=6度,所以,3点25分时针与分针的夹角为
6. ∵∠BOC+∠BOD=180°;∠BOC-∠BOD=20° ∴∠BOC =100°;∠BOD =80°;∴∠BOE =140°
7. 画出2个60度一个45度即可。
8. 20米
第三节 角(二)角的度量与画法
一. 教学内容:
角的度量与画法
【知识点讲解】
1. 角的度量:按对线、对中、度数的步骤用量角器量出角的度数
2. 角的度数计算:角的单位是度分秒,都是60进制,可以比照时间中的时分秒理解,分别用“°”、“ ’”、“ ””来表示。
3. 余角、补角的概念与性质:如果两个角的和是90度(或直角)时,叫做两个角互余;
4. 如果两个角的和是180度(或平角)时,叫做两个角互补。
(补角同理)
性质:同角(或等角)的余角相等;同角(或等角)的补角相等
(补角同理)
5. 能利用三角板画出15°、30°、45°、60°、75°、90°等11种特殊角
6. 会用尺规画一个角等于已知角,角的和、差的画法。
【技能要求】
1. 掌握度、分、秒的计算。
2. 逐步掌握学过的几何图形的表示方法,懂得学过的几何语句,能由这些语句准确、整洁地画出图形。认识学过的图形,会用语句描述这些简单的几何图形。
【典型例题】
例1. 将33.72°用度、分、秒表示。
解:
33.72°=33°+(0.72×60′)=33°+43.2′=33°+43′+(0.2′×60″)=33°43′12″
例2. 用度表示152°13′30″。
解:152°13′30″=152°+(13)′=152°+13.5′=152°+()°=152.225°
例3. 判断下列计算的对错,对的画“√”,错的说明错在哪里,并改正。
(1)31°56′÷3=10°52′
(2)138°29′+44°49′=183°18′
(3) 13.5°×3=39.50
(4)21.36°-18°30′=3.14°.
解:
(1)错,因为用1°=100′计算的。
应改为:31°56′÷3=(30°+114′+120″) ÷3=10°38′40″
(2)(√)。
(3)错,本题是十进制小数,要按一般乘法规则进位,应改为13.5°×3=40.5°。
(4)错,因为被减数与减数单位不同,不能相减。
应改为:21.36°-18°30′=21°+0.36×60′-18°30’ =21°21′+0.6×60″-18°30′=21°21′36″-18°30′=20°81′36″-18°30′=2°51′36″
例4. 已知∠α=22.68°,∠β=18°41′55″,求∠α与∠β的差(结果用度、分、秒表示)
分析:因为结果要求用度、分、秒表示,所以,先将∠α表示为度分秒的形式:
22.68°=22°+0.68°=22°+0.68×60’=22°+40.8’=22°+40’+0.8×60″=22°+40’+48″=22°40’48’’;然后求∠α-∠β=22°40’48’’-18°41’55’’(1)=21°99’108″-18°41’55’’(2)=3°58’53″(3)
注意:两角度相加减时,“度”与“度”、“分”与“分”、“秒”与“秒”分别相加减,如第(3)步;当被减数中的“秒”不够减时(如第(1)步),可从40′中借来1’,化作60″,22°40′48″就变为22°39′108″;当被减数中的“分”不够减时(如第(2)步),可从22°借1°,化作60′,这时,22°39′108″就变为21°99′108″。
例5. 求24°35′43″与121°48′56″的和(结果精确到分)
解:24°35′43″+121°48′56″=145°83′99″ (1)=145°84′39″ (2) =146°24′39″ (3) ≈146°25′ (4)
注意:
①本题可直接求得两角之和为145°83′99″,但是99″要变成1′39″(如第(2)步),84′要变成1°24′(如第(3)步)。
②精确到分时,将不足30″的舍去,30″及超过30″的进为1′;精确到度时,则将不足30′的舍去,30′及超过30′的进为1°。③由低级单位向高级单位转化或由高级单位向低级单位转化,要逐级进行,千万不要“越级”。
例6. 把1个周角7等分,求每份角的度数。(精确到分)
分析:1个周角为360°,那么把它7等分,每份角的度数可由360°÷7计算得出。
解:360°÷7=51°+3°÷7 =51°+180′÷7 ≈51°+26′=51°26′
注意:对分的十进制小数来说,仍按四舍五入方法进行近似计算。如25.7′≈26′,
8.4′≈8′。
例7.一个角比它的余角的多14°,求这个角的补角。
解:设这个角的度数为x°,则它的余角为(90-x) °,补角为(180-x) °,
由题意可得,x- (90-x)=14, 解方程得x=33,∴ 180-x=180-33=147°.
答:这个角的补角为147°。
例8.一个角是另一个角的3倍,且小角的余角与大角的补角之差为20°,求这两个角的度数。
解:设大角的度数为x, 则它的补角为(180-x) °,设小角为y°, 则它的余角为(90-y) °,
由题意可得
解方程组得
答:小角为55°,大角为165°。
说明:因为互余两角与互补两角之间的关系是数量关系,所以解这类计算题时,常用代数中的列方程解应用题的方法来做是很好的方法。
例9. 下午2点到2点30分,时钟的时针和分针各转过了多少度?
分析:时钟被分成12个大格时,相当于把圆周12等分,每一等份等于30°,分针转360°时,时针转一大格即30°。
解:时针是0. 5°×30=15°,分针是6°×30=180°
答:时针转了15°,分针转了180°。
例10. 在时刻8:25,时钟上的时针和分针之间的夹角是多少度?
分析:时针偏离0.5°×25=12.5°,分针6°×25=150°,8点时时针在分针前,30°×8=240°,240°—150°=90°,夹角为90°+12.5°=102.5°
例11. 已知OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1、∠3、∠4的度数。
解:∵OB是平分线
∴∠1=∠2
∵设一份角为x
∴∠2=∠1=x,∠3=3x,∠4=4x
∴x=40
∴∠1=40°,∠3=120°,∠4=160°
【模拟试题】(答题时间:30分钟)
1. 把30°23’45’’化成度;求46.83°化成度分秒,求109°11’4’’÷7
2. 一个角的补角是它的余角的4倍,求这个角的补角
3. 已知AOC为一直线,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,
∠DOE=72°,求∠EOC的度数。
4. 计算
5. 求时钟表面3点25分时,时针与分针的夹角是多少度?
6. 直线AB与CD相交于点O,OE平分∠AOC,∠BOC-∠BOD=20°,求∠BOE的度数。
7. 用三角板画出165°角
8. 甲乙两名学生在操场上,从同一旗杆处出发,甲向北走18米,乙向东走16米,以后又向北走6米,用1厘米代表2米,画出方位图,测量并计算甲乙的距离。
【试题答案】
1. 答30°23’45’’=:46.83°= 2. 设这个角的补角是X,根据题意得;X=4[90-(180-X)],解得;X=120;所以,这个角的补角是120°。
3.解法1 设∠AOB=x°,∠BOC=y°,则
解法2.设角EOC=2X,则角BOE=X, 角AOD=72°-X, 得方程;2(72°-X)+3X=180° 解得;X=36°,所以,角EOC=72度。
4. 5.时针每分钟转的角度是360°/(12*60)=1/2度,分针每分钟转360°/60=6度,所以,3点25分时针与分针的夹角为
6. ∵∠BOC+∠BOD=180°;∠BOC-∠BOD=20° ∴∠BOC =100°;∠BOD =80°;∴∠BOE =140°
7. 画出2个60度一个45度即可。
8. 20米
