人教A版高中数学必修二 3.1.1 方程的根与函数的零点(共37张PPT)
文档属性
| 名称 | 人教A版高中数学必修二 3.1.1 方程的根与函数的零点(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 15:07:31 | ||
图片预览



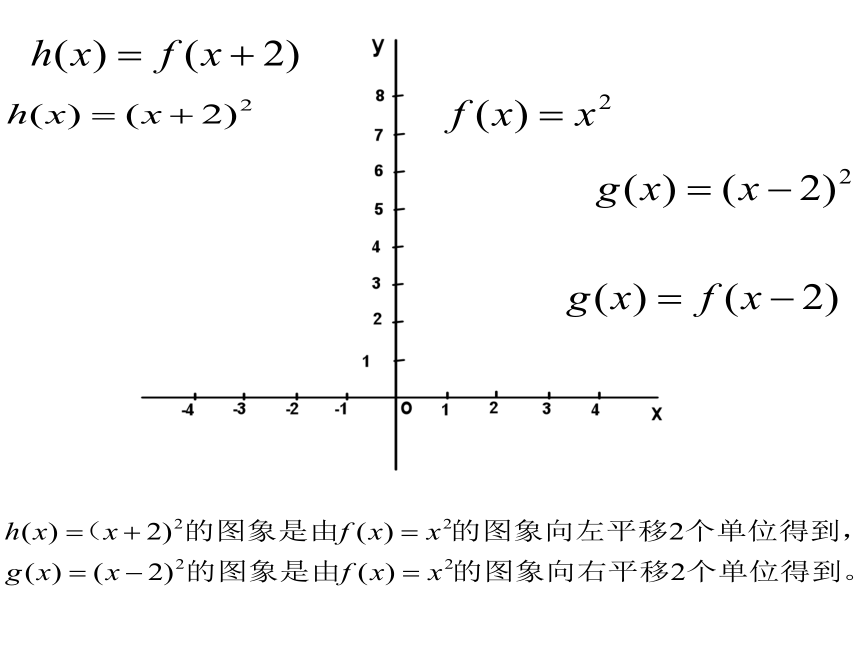

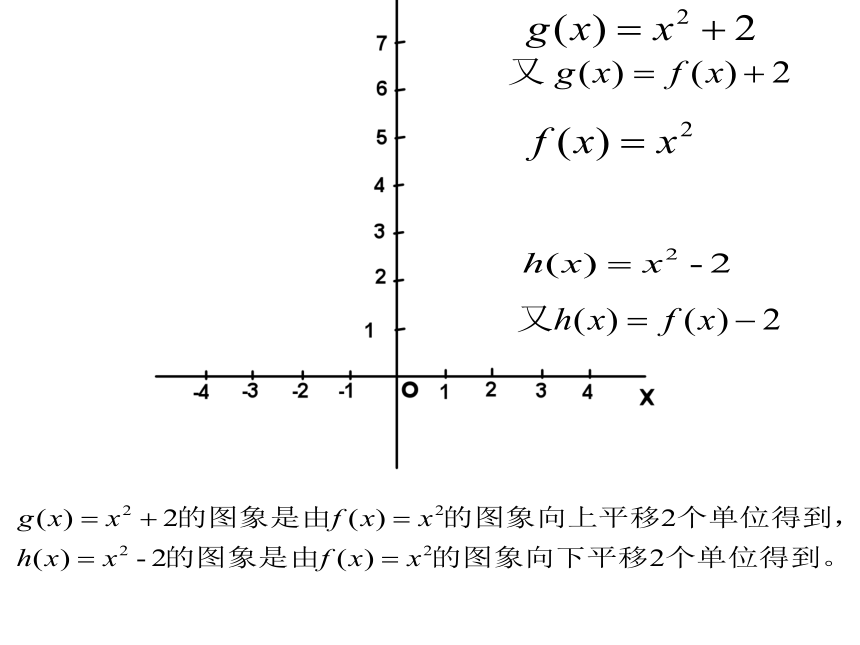


文档简介
(共37张PPT)
函数的图象变换
华罗庚
数少形时少直观
形少数时难入微
数形结合百般好
数形分离万事休
引入:前面我们学习了指数函数、对数函数的图象和性质,其中涉及到许多与图象有关的问题或利用函数图象(数形结合)来解决的问题。其实,在初中就涉及到函数图象的平移问题。今天我们就来梳理一下函数图象的变换问题。
有关数形结合的重要性我国著名数学家华罗庚早有论断
下面我们就从具体的实例出发,利用特殊到一般的思想总结函数图象变换的规律,并学习其简单的应用。
例1.画出下列函数的图象,
并说明它们的关系:
(1)
f(x)=x2
(2)
g(x)=(x+2)2
(3)
h(x)=(x-2)2
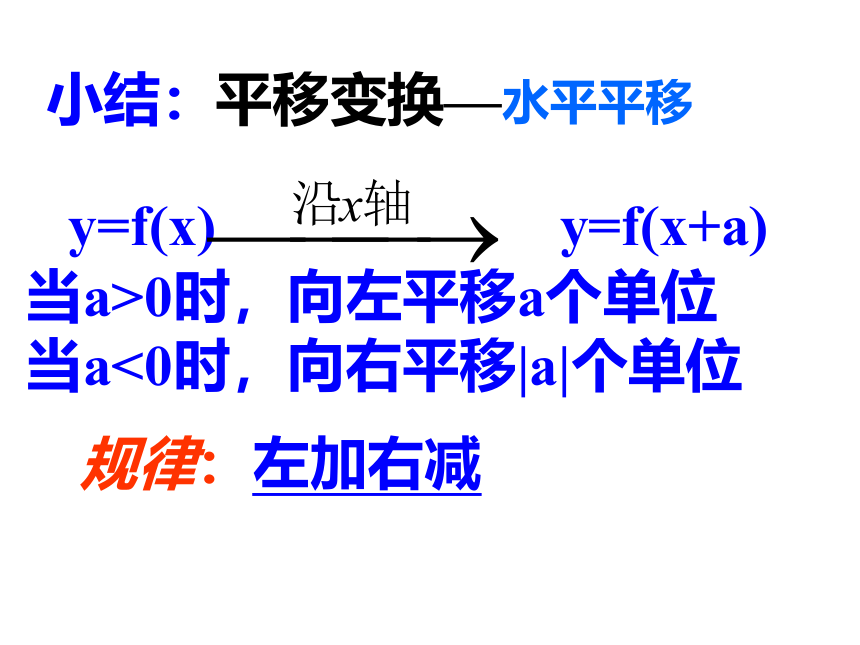
规律:左加右减
平移变换—水平平移
y=f(x)
y=f(x+a)
当a>0时,向左平移a个单位
当a<0时,向右平移|a|个单位
小结:
例2:画出下列函数的图象,
并说明它们的关系:
(1)
f(x)=x2
(2)
g(x)=x2+2
(3)
h(x)=x2-2
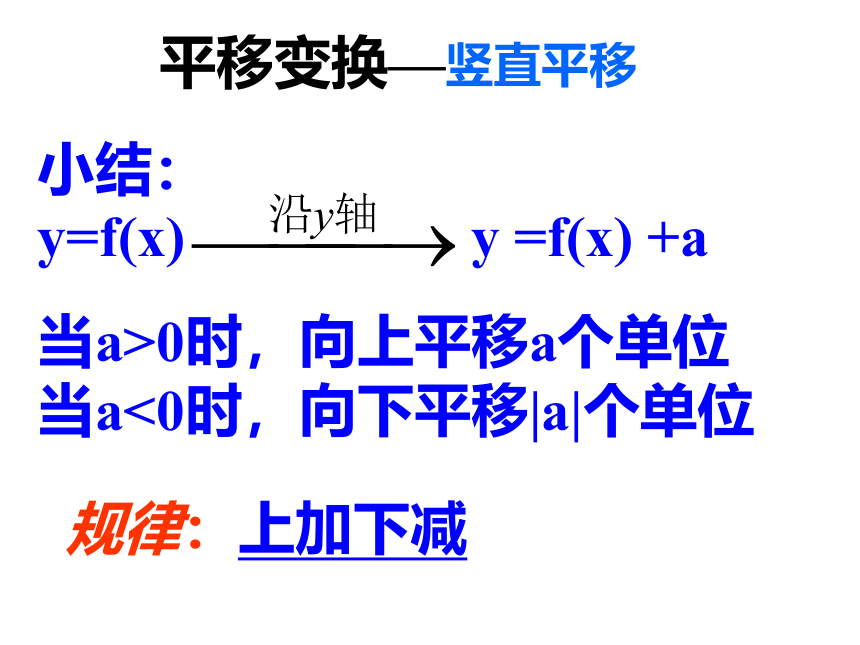
规律:上加下减
小结:
y=f(x)
y
=f(x)
+a
当a>0时,向上平移a个单位当a<0时,向下平移|a|个单位
平移变换—竖直平移
练习:
的图象变化得到?此函数的对称中心是什么?
分析:一次分式函数是由反比例函数经过平移得到。那如何得到平移过程呢?
常数分离!!!
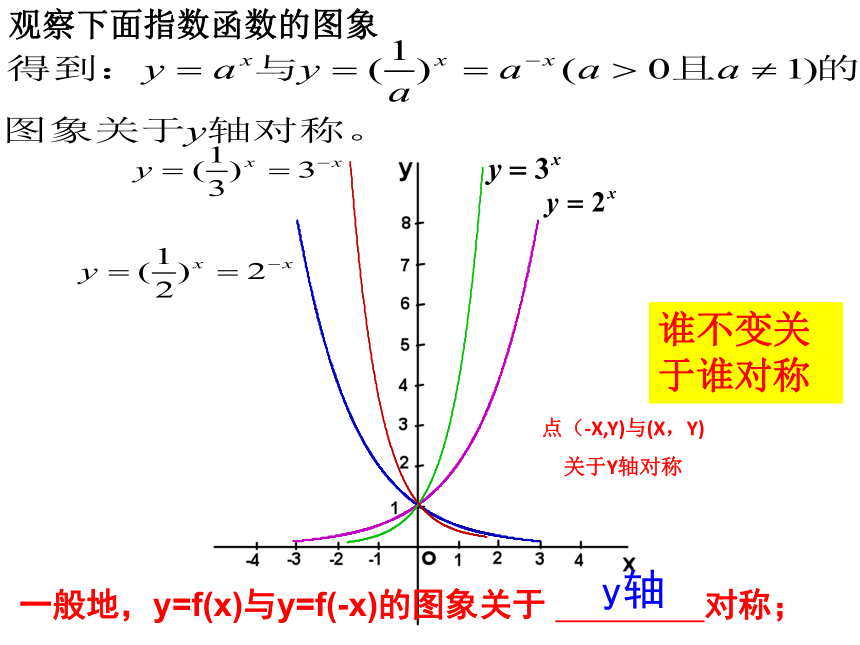
观察下面指数函数的图象
一般地,y=f(x)与y=f(-x)的图象关于
对称;
y轴
点(-X,Y)与(X,Y)
关于Y轴对称
谁不变关于谁对称
x
y
O
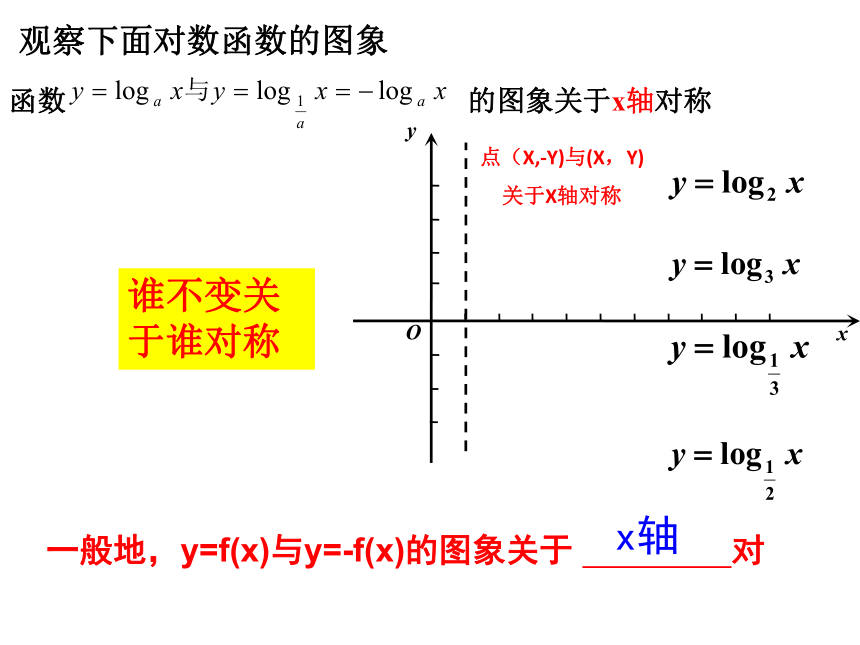
观察下面对数函数的图象
函数
的图象关于x轴对称
点(X,-Y)与(X,Y)
关于X轴对称
一般地,y=f(x)与y=-f(x)的图象关于
对称;
x轴
谁不变关于谁对称
例3.①画函数
并说明
由
的图像怎样变换而得到?
②画函数
并说由
的图像怎样变换而得到?
例3.①画函数
并说明
由
的图像怎样变换而得到?
例3.①画函数
并说明
由
的图像怎样变换而得到?
小结:
1、y=f(x)?y=f(|x|),保留y=f(x)图象在y轴右侧部分,并将y=f(x)在y轴右侧部分翻折到y轴左侧。
2、
y=f(x)?y=|f(x)|,将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。
翻折变换
练习:
函数
的单调增区间为
x
y
O
函
数
y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|
a>0时向左平移a个单位;a<0时向右平移|a|个单位.
a>0时向上平移a个单位;a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
保留y=f(x)图象在y轴右侧部分,将y=f(x)图象在y轴右侧部分沿y轴翻折到y轴左侧。
将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。
总结:
分析:作函数图象的方法有:列表描点法(列表,描点,连线)和图象变换法(平移变换、对称变换、翻折变换)
x
y
O
x
y
O
课堂练习
课堂总结:
本节课从特殊到一般的思路学习函数图象的三种变换(平移变换、对称变换、翻折变换)及其应用。利用图象变换解题,关键是理清图象变换的过程,掌握好基本初等函数的图象及变换的实质(要通过具体的实例作为载体来理解掌握三种变换)。在后续的学习中我们将进一步学习它的应用。
谢谢!!!
函数的图象变换
华罗庚
数少形时少直观
形少数时难入微
数形结合百般好
数形分离万事休
引入:前面我们学习了指数函数、对数函数的图象和性质,其中涉及到许多与图象有关的问题或利用函数图象(数形结合)来解决的问题。其实,在初中就涉及到函数图象的平移问题。今天我们就来梳理一下函数图象的变换问题。
有关数形结合的重要性我国著名数学家华罗庚早有论断
下面我们就从具体的实例出发,利用特殊到一般的思想总结函数图象变换的规律,并学习其简单的应用。
例1.画出下列函数的图象,
并说明它们的关系:
(1)
f(x)=x2
(2)
g(x)=(x+2)2
(3)
h(x)=(x-2)2
规律:左加右减
平移变换—水平平移
y=f(x)
y=f(x+a)
当a>0时,向左平移a个单位
当a<0时,向右平移|a|个单位
小结:
例2:画出下列函数的图象,
并说明它们的关系:
(1)
f(x)=x2
(2)
g(x)=x2+2
(3)
h(x)=x2-2
规律:上加下减
小结:
y=f(x)
y
=f(x)
+a
当a>0时,向上平移a个单位当a<0时,向下平移|a|个单位
平移变换—竖直平移
练习:
的图象变化得到?此函数的对称中心是什么?
分析:一次分式函数是由反比例函数经过平移得到。那如何得到平移过程呢?
常数分离!!!
观察下面指数函数的图象
一般地,y=f(x)与y=f(-x)的图象关于
对称;
y轴
点(-X,Y)与(X,Y)
关于Y轴对称
谁不变关于谁对称
x
y
O
观察下面对数函数的图象
函数
的图象关于x轴对称
点(X,-Y)与(X,Y)
关于X轴对称
一般地,y=f(x)与y=-f(x)的图象关于
对称;
x轴
谁不变关于谁对称
例3.①画函数
并说明
由
的图像怎样变换而得到?
②画函数
并说由
的图像怎样变换而得到?
例3.①画函数
并说明
由
的图像怎样变换而得到?
例3.①画函数
并说明
由
的图像怎样变换而得到?
小结:
1、y=f(x)?y=f(|x|),保留y=f(x)图象在y轴右侧部分,并将y=f(x)在y轴右侧部分翻折到y轴左侧。
2、
y=f(x)?y=|f(x)|,将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。
翻折变换
练习:
函数
的单调增区间为
x
y
O
函
数
y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|
a>0时向左平移a个单位;a<0时向右平移|a|个单位.
a>0时向上平移a个单位;a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
保留y=f(x)图象在y轴右侧部分,将y=f(x)图象在y轴右侧部分沿y轴翻折到y轴左侧。
将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。
总结:
分析:作函数图象的方法有:列表描点法(列表,描点,连线)和图象变换法(平移变换、对称变换、翻折变换)
x
y
O
x
y
O
课堂练习
课堂总结:
本节课从特殊到一般的思路学习函数图象的三种变换(平移变换、对称变换、翻折变换)及其应用。利用图象变换解题,关键是理清图象变换的过程,掌握好基本初等函数的图象及变换的实质(要通过具体的实例作为载体来理解掌握三种变换)。在后续的学习中我们将进一步学习它的应用。
谢谢!!!
