六年级上册数学课件-4.1 圆的周长冀教版 (共31张PPT)
文档属性
| 名称 | 六年级上册数学课件-4.1 圆的周长冀教版 (共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览






文档简介
圆
的
周
长
车轮转动一周走的距离就是车轮的周长。
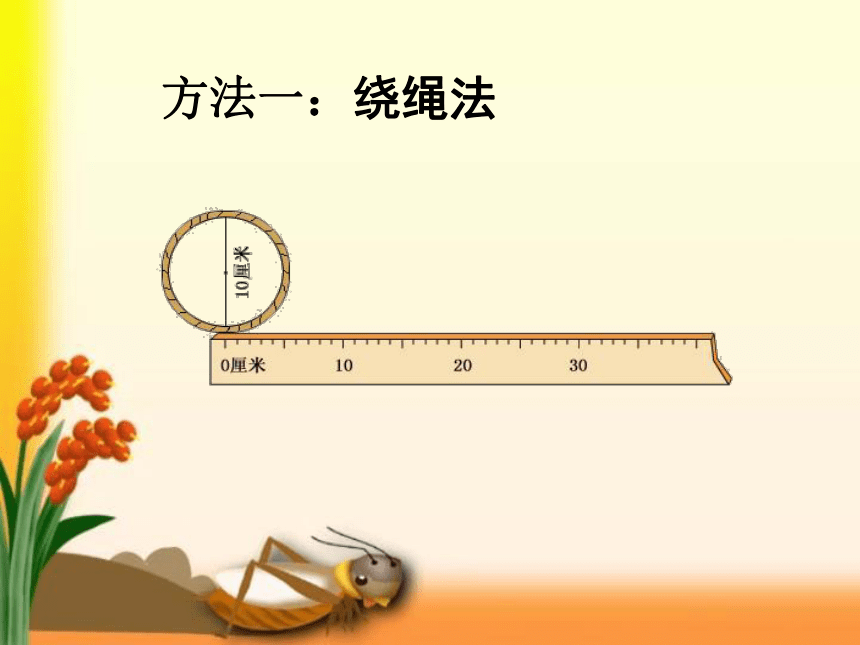
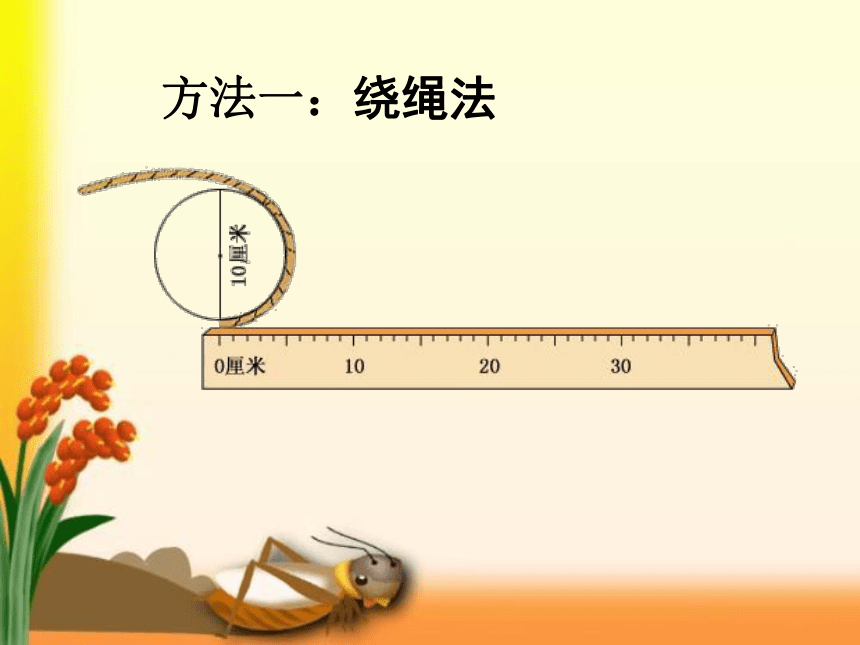
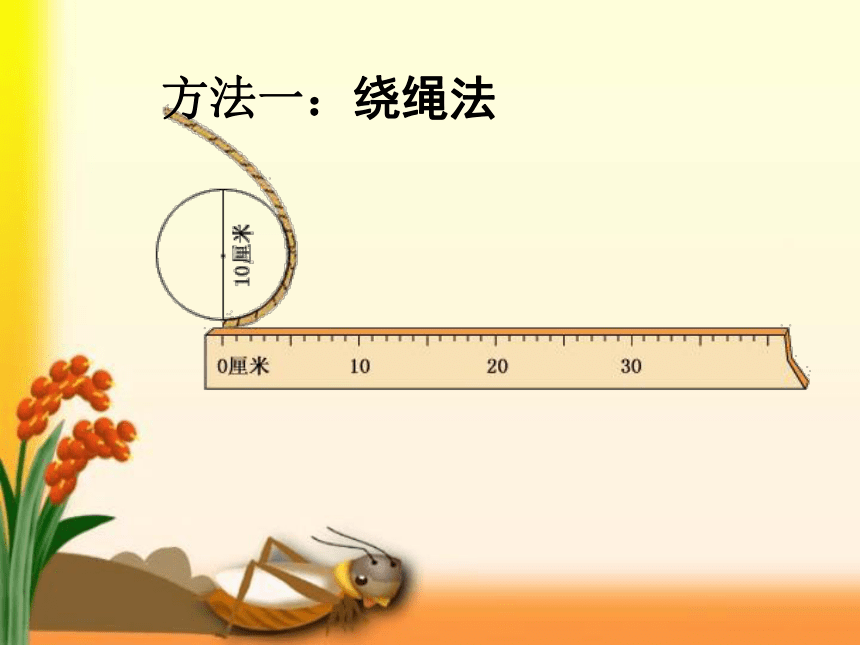
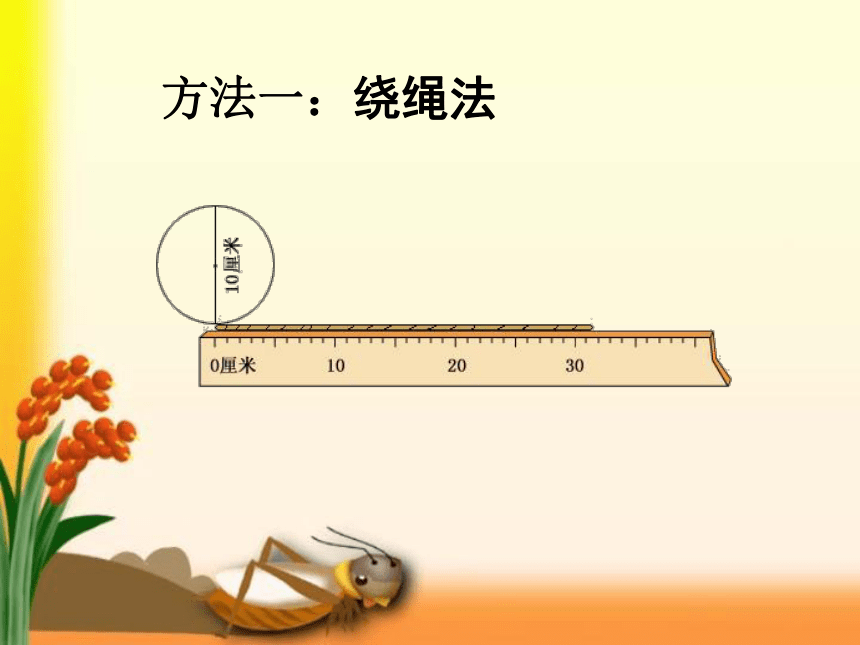
围成圆的曲线的长叫做圆的周长。
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
0cm
10
20
30
40
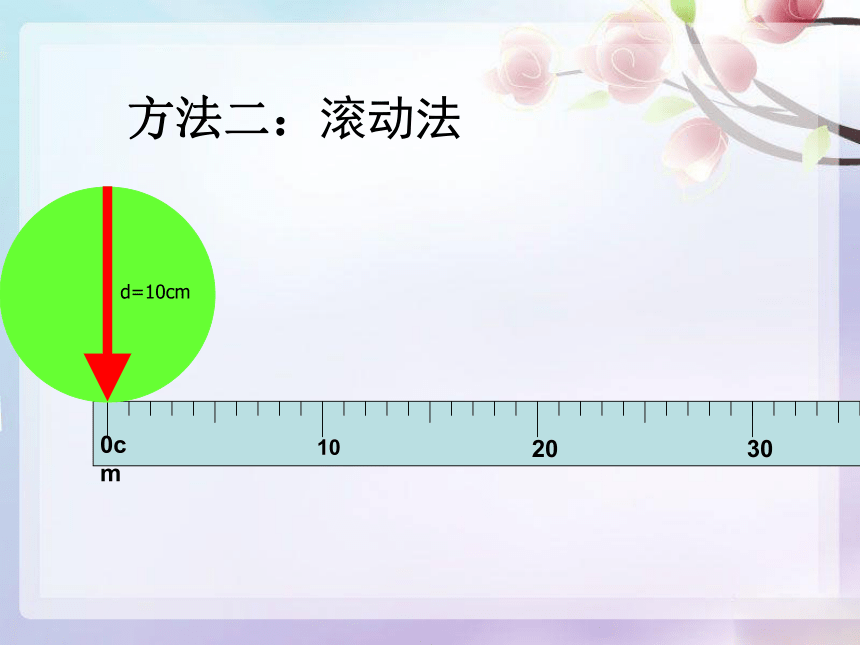
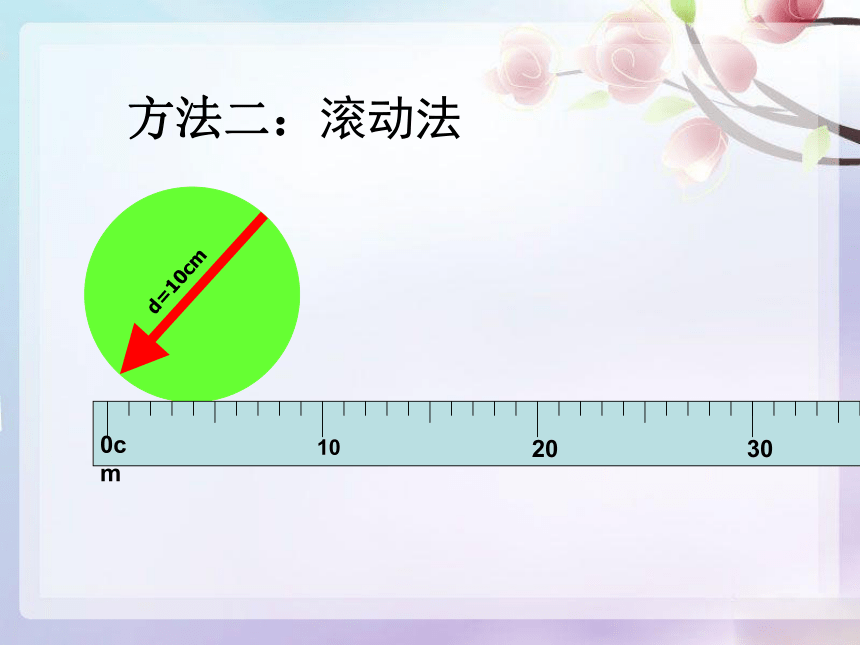
方法二:滚动法
d=10cm
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
圆向右滚动一周,走过的距离就是圆的周长。
转化法:化曲为直
请同学们大胆猜测一下,圆的周长大约是它直径的几倍?
探究活动要求:
1、小组分工合作,找三个大小不同的圆形物品,分别测量它们
的周长和直径。
2、计算出周长除以直径的结果,填在表中。(可用计算器计算,
除不尽的保留两位小数)
物品
周长
直径
周长÷直径
观察计算的结果,你发现了什么?
————————————————
任何圆的周长总是它直径的3倍多一些。这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母“π (读pài)”表示。他是一个无限不循环小数,π= 3.1415926……但在实际应用中一般只取它的近似值,即π≈3.14。
祖冲之
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值的计算精确到7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
祖冲之,范阳遒县人(今河北涞水县)人,南北朝时期杰出的数学家、天文学家和机械专家。
C = πd
C = 2πr
圆的周长 = 直径×圆周率
圆的周长÷圆的直径=圆周率
求下面圆的周长。(只列式,不计算 )
d=2厘米
r=2厘米
3.14×2
2×3.14×2
法官判案,明察秋毫
1、圆越大,圆周率越大。( )
2、圆的周长是它的直径的π倍。( )
√
×
我的收获
谈谈你的收获!
一面圆镜的镜面直径是25厘米,在它的边缘镶嵌着一根金属条,这根金属条的长至少是多少厘米?
3.14×25=78.5(cm)
答:这根金属条的长至少是78.5厘米。
学以致用:
2、在一个圆形亭子里,小丽走完它的直径需用12步,每步长大约是55厘米,这个圆形亭子的周长大约是多少?
3.14×12×55=2072.4(厘米)
答:这个圆的周长大约是2072.4厘米。
求出聪聪和爸爸的车轮的周长各是多少?只列式,不计算。
r=33厘米
3.14×56
2×3.14×33
d=56cm
r=33cm
的
周
长
车轮转动一周走的距离就是车轮的周长。
围成圆的曲线的长叫做圆的周长。
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
方法一:绕绳法
0cm
10
20
30
40
方法二:滚动法
d=10cm
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
方法二:滚动法
10
20
30
40
d=10cm
0cm
圆向右滚动一周,走过的距离就是圆的周长。
转化法:化曲为直
请同学们大胆猜测一下,圆的周长大约是它直径的几倍?
探究活动要求:
1、小组分工合作,找三个大小不同的圆形物品,分别测量它们
的周长和直径。
2、计算出周长除以直径的结果,填在表中。(可用计算器计算,
除不尽的保留两位小数)
物品
周长
直径
周长÷直径
观察计算的结果,你发现了什么?
————————————————
任何圆的周长总是它直径的3倍多一些。这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母“π (读pài)”表示。他是一个无限不循环小数,π= 3.1415926……但在实际应用中一般只取它的近似值,即π≈3.14。
祖冲之
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值的计算精确到7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
祖冲之,范阳遒县人(今河北涞水县)人,南北朝时期杰出的数学家、天文学家和机械专家。
C = πd
C = 2πr
圆的周长 = 直径×圆周率
圆的周长÷圆的直径=圆周率
求下面圆的周长。(只列式,不计算 )
d=2厘米
r=2厘米
3.14×2
2×3.14×2
法官判案,明察秋毫
1、圆越大,圆周率越大。( )
2、圆的周长是它的直径的π倍。( )
√
×
我的收获
谈谈你的收获!
一面圆镜的镜面直径是25厘米,在它的边缘镶嵌着一根金属条,这根金属条的长至少是多少厘米?
3.14×25=78.5(cm)
答:这根金属条的长至少是78.5厘米。
学以致用:
2、在一个圆形亭子里,小丽走完它的直径需用12步,每步长大约是55厘米,这个圆形亭子的周长大约是多少?
3.14×12×55=2072.4(厘米)
答:这个圆的周长大约是2072.4厘米。
求出聪聪和爸爸的车轮的周长各是多少?只列式,不计算。
r=33厘米
3.14×56
2×3.14×33
d=56cm
r=33cm
