2020_2021学年高中数学第二章解三角形质量评估1含解析北师大版必修5(Word含解析)
文档属性
| 名称 | 2020_2021学年高中数学第二章解三角形质量评估1含解析北师大版必修5(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 203.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 16:37:13 | ||
图片预览




文档简介
第二章单元质量评估(一)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.在△ABC中,已知a=2,则bcosC+ccosB等于(
)
A.1
B.
C.2
D.4
2.已知△ABC中,c=6,a=4,B=120°,则b等于(
)
A.76
B.2
C.27
D.2
3.在△ABC中,A=60°,b=1,S△ABC=
,则=(
)
A.
B.
C.
D.2
4.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,设向量p=(a+c,b),q=(b-a,c-a).若p∥q,则角C的大小为(
)
A.
B.
C.
D.
5.在△ABC中,A=60°,AC=16,面积S=220,则BC的长为(
)
A.20
B.75
C.51
D.49
6.在锐角△ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于(
)
A.
B.
C.
D.
7.若==,则△ABC是(
)
A.等边三角形
B.有一内角是30°的直角三角形
C.等腰直角三角形
D.有一内角是30°的等腰三角形
8.设a,b,c为△ABC的三边,且关于x的方程(a2+bc)x2+2x+1=0有两个相等的实数根,则A的度数是(
)
A.120°
B.90°
C.60°
D.30°
9.在锐角三角形ABC中,已知A=2C,则的范围是(
)
A.(0,2)
B.(,2)
C.(,)
D.(,2)
10.在△ABC中,已知BC=5,外接圆半径为5.若·=,则△ABC的周长为(
)
A.11
B.9
C.7
D.5
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,且b=3,c=1,A=2B,则a=(
)
A.4
B.3
C.2
D.2
12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20
n
mile,随后货轮按北偏西30°的方向航行30
min后,又测得灯塔在货轮的东北方向,则货轮的速度为(
)
A.20(+)n
mile/h
B.20(-)n
mile/h
C.20(+)n
mile/h
D.20(-)n
mile/h
二、填空题(本大题共4小题,每小题5分,共20分,请把答案填写在题中横线上)
13.在△ABC中,AC=,A=45°,C=75°,则BC的长为(
)
14.在△ABC中,三个内角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC的值为(
).
15.在△ABC中,若S△ABC=12,ac=48,c-a=2,则b=(
).
16.在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为3-,则∠BAC=(
).
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)·(a-b+c)=ac.
(1)求B;
(2)若sinAsinC=,求C.
18.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
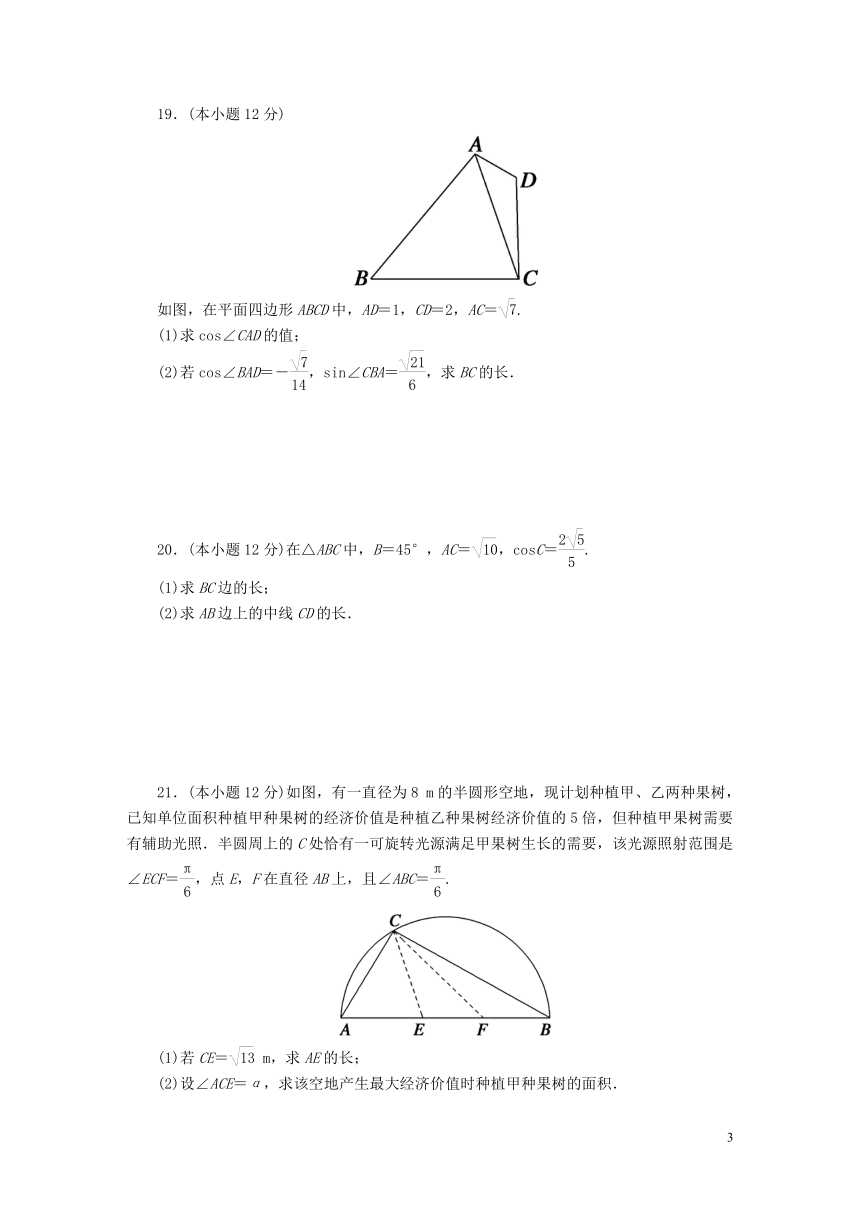
19.(本小题12分)
如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(1)求cos∠CAD的值;
(2)若cos∠BAD=-,sin∠CBA=,求BC的长.
20.(本小题12分)在△ABC中,B=45°,AC=,cosC=.
(1)求BC边的长;
(2)求AB边上的中线CD的长.
21.(本小题12分)如图,有一直径为8
m的半圆形空地,现计划种植甲、乙两种果树,已知单位面积种植甲种果树的经济价值是种植乙种果树经济价值的5倍,但种植甲果树需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲果树生长的需要,该光源照射范围是∠ECF=,点E,F在直径AB上,且∠ABC=.
(1)若CE=
m,求AE的长;
(2)设∠ACE=α,求该空地产生最大经济价值时种植甲种果树的面积.
22.(本小题12分)在△ABC中,AD是BC边的中线,AB2+AC2+AB×AC=BC2,且△ABC的面积为.
(1)求∠BAC的大小及·的值;
(2)若AB=4,求AD的长.
第二章单元质量评估(一)(答案版)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.在△ABC中,已知a=2,则bcosC+ccosB等于( C )
A.1
B.
C.2
D.4
解析:由余弦定理,得bcosC+ccosB=b·+c·==a=2.
2.已知△ABC中,c=6,a=4,B=120°,则b等于( B )
A.76
B.2
C.27
D.2
解析:由余弦定理,得b2=a2+c2-2accosB=76,所以b=2.
3.在△ABC中,A=60°,b=1,S△ABC=
,则=( B )
A.
B.
C.
D.2
解析:依题意得S△ABC=bcsin60°=,得c=4,由余弦定理得a==,由正弦定理得===.
4.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,设向量p=(a+c,b),q=(b-a,c-a).若p∥q,则角C的大小为( B )
A.
B.
C.
D.
解析:∵p∥q,∴(a+c)(c-a)-b(b-a)=0,即a2+b2-c2=ab,∴cosC===,∴C=.
5.在△ABC中,A=60°,AC=16,面积S=220,则BC的长为( D )
A.20
B.75
C.51
D.49
解析:因为S=AC·ABsinA=×16×AB×sin60°=4AB=220,所以AB=55.再用余弦定理求得BC=49.
6.在锐角△ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于( D )
A.
B.
C.
D.
解析:由已知及正弦定理得2sinAsinB=sinB,因为sinB>0,所以sinA=.又A∈,所以A=.
7.若==,则△ABC是( C )
A.等边三角形
B.有一内角是30°的直角三角形
C.等腰直角三角形
D.有一内角是30°的等腰三角形
解析:∵=,∴acosB=bsinA,∴2RsinAcosB=2RsinBsinA,
又2RsinA≠0,∴cosB=sinB,∴B=45°.同理C=45°,故A=90°.
8.设a,b,c为△ABC的三边,且关于x的方程(a2+bc)x2+2x+1=0有两个相等的实数根,则A的度数是( C )
A.120°
B.90°
C.60°
D.30°
解析:∵由题意可知题中方程的判别式Δ=4(b2+c2)-4(a2+bc)=0,∴b2+c2-a2=bc,cosA=.
又∵0°9.在锐角三角形ABC中,已知A=2C,则的范围是( C )
A.(0,2)
B.(,2)
C.(,)
D.(,2)
解析:===2cosC,又A+B+C=π,A=2C,∴10.在△ABC中,已知BC=5,外接圆半径为5.若·=,则△ABC的周长为( A )
A.11
B.9
C.7
D.5
解析:设角A,B,C的对边分别为a,b,c.由题意,得=2×5,∴sinA=,∴A=60°或120°.∵·=,∴A=60°,bccos60°=,∴bc=11.∵a2=b2+c2-bc=(b+c)2-3bc=75,∴(b+c)2=108,∴a+b+c=5+6=11.
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,且b=3,c=1,A=2B,则a=( D )
A.4
B.3
C.2
D.2
解析:∵A=2B,∴C=π-(A+B)=π-3B,sinC=sin3B.由正弦定理知==,∴sinB=3sin3B ①,∵sin3B=sin(2B+B)=sin2BcosB+cos2BsinB=2sinBcos2B+(1-2sin2B)sinB=2sinB-2sin3B+sinB-2sin3B=3sinB-4sin3B ②.把②代入①,得sinB=3(3sinB-4sin3B).分析知B∈,∴sinB≠0,∴sinB=,cosB=,∴由=,得a=6cosB=2.
12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20
n
mile,随后货轮按北偏西30°的方向航行30
min后,又测得灯塔在货轮的东北方向,则货轮的速度为( B )
A.20(+)n
mile/h
B.20(-)n
mile/h
C.20(+)n
mile/h
D.20(-)n
mile/h
解析:由题意可知∠SMN=15°+30°=45°,MS=20,∠MNS=45°+(90°-30°)=105°,
∴∠MSN=180°-105°-45°=30°,
设货轮每小时航行x
n
mile,则MN=x,由正弦定理,得=,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=,∴x=20(-),故选B.
二、填空题(本大题共4小题,每小题5分,共20分,请把答案填写在题中横线上)
13.在△ABC中,AC=,A=45°,C=75°,则BC的长为.
解析:由A=45°,C=75°,知B=60°.由正弦定理,得=,所以BC=·AC=×=.
14.在△ABC中,三个内角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC的值为.
解析:在△ABC中,由余弦定理,得cosA=,∴bccosA=,
同理accosB=,abcosC=,∴原式==.
15.在△ABC中,若S△ABC=12,ac=48,c-a=2,则b=2或2.
解析:由S△ABC=acsinB得sinB=,∴B=60°或120°.
由余弦定理得b2=a2+c2-2accosB=(a-c)2+2ac-2accosB=22+2×48-2×48cosB,
∴b2=52或148,即b=2或2.
16.在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为3-,则∠BAC=60°.
解析:∵∠ADB=120°,∴∠ADC=60°,又S△ADC=×AD×DC×sin∠ADC=×2×DC×=DC=3-,∴DC=2-2.∵BD=DC,∴BD=-1,得BC=3-3.在△ABD中,由余弦定理,得AB2=AD2+BD2-2AD·BD·cos120°=4+3-2+1+4(-1)×=6,在△ACD中,由余弦定理,得AC2=AD2+DC2-2AD·DC·cos60°=4+12-8+4-8(-1)×=24-12,在△ABC中,由余弦定理,得cos∠BAC====,∴∠BAC=60°.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)·(a-b+c)=ac.
(1)求B;
(2)若sinAsinC=,求C.
解:(1)因为(a+b+c)(a-b+c)=ac,所以a2+c2-b2=-ac.
由余弦定理得cosB==-,因此B=120°.
(2)由(1)知A+C=60°,所以cos(A-C)=cosAcosC+sinAsinC=cosAcosC-sinAsinC+2sinAsinC=cos(A+C)+2sinAsinC=+2×=,故A-C=30°或A-C=-30°,因此C=15°或C=45°.
18.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
解:(1)证明:由已知得sinB(sinAcosC+cosAsinC)=sinAsinC,∴sinBsin(A+C)=sinAsinC,
则sin2B=sinAsinC,再由正弦定理,可得b2=ac,∴a,b,c成等比数列.
(2)若a=1,c=2,则b2=ac=2,∴cosB==,∴sinB==,
∴△ABC的面积S=acsinB=×1×2×=.
19.(本小题12分)
如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(1)求cos∠CAD的值;
(2)若cos∠BAD=-,sin∠CBA=,求BC的长.
解:(1)在△ADC中,由余弦定理,得cos∠CAD=.
故由题设知,cos∠CAD==.
(2)设∠BAC=α,则α=∠BAD-∠CAD.
因为cos∠CAD=,cos∠BAD=-,
所以sin∠CAD===,sin∠BAD===.
于是sinα=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=×-×=.
在△ABC中,由正弦定理,=.故BC===3.
20.(本小题12分)在△ABC中,B=45°,AC=,cosC=.
(1)求BC边的长;
(2)求AB边上的中线CD的长.
解:(1)由cosC=,得sinC=,sinA=sin(180°-45°-C)=sin(135°-C)=(cosC+sinC)=.
由正弦定理,得BC=·sinA=×=3.
(2)由正弦定理,得AB=·sinC=×=2.BD=AB=1.
由余弦定理,得CD==
=.
21.(本小题12分)如图,有一直径为8
m的半圆形空地,现计划种植甲、乙两种果树,已知单位面积种植甲种果树的经济价值是种植乙种果树经济价值的5倍,但种植甲果树需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲果树生长的需要,该光源照射范围是∠ECF=,点E,F在直径AB上,且∠ABC=.
(1)若CE=
m,求AE的长;
(2)设∠ACE=α,求该空地产生最大经济价值时种植甲种果树的面积.
解:(1)由已知,点C在以AB为直径的半圆周上,所以△ACB为直角三角形,
因为AB=8,∠ABC=,所以∠A=,AC=4,
在△ACE中,CE2=AC2+AE2-2AC×AEcos∠A,且CE=,所以13=16+AE2-4AE,
解得AE=1或AE=3.
(2)因为∠ACB=,∠ECF=,所以∠ACE=α∈,
所以∠AFC=π-∠A-∠ACF=π--=-α,
在△ACF中,===.
所以CF=.
在△ACE中,==,
所以CE=.
若要产生最大经济价值,则△ECF的面积最大.
S△ECF=CE×CFsin∠ECF==,
因为α∈,所以0≤sin≤1,
所以当α=时,S△ECF取得最大值,为4
m2,即种植甲种果树的面积为4
m2时,该空地产生的经济价值最大.
22.(本小题12分)在△ABC中,AD是BC边的中线,AB2+AC2+AB×AC=BC2,且△ABC的面积为.
(1)求∠BAC的大小及·的值;
(2)若AB=4,求AD的长.
解:(1)在△ABC中,由AB2+AC2+AB×AC=BC2,可得=-=cos∠BAC,故∠BAC=120°.
因为S△ABC=AB×AC×sin∠BAC=×AB×AC×sin120°=,
即×AB×AC×=,所以AB×AC=4.
所以·=||×||×cos120°=||×||×=4×=-2.
(2)由AB=4,AB×AC=4,得AC=1.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB×AC×cos∠BAC=16+1-2×4×1×=21,
即BC=,
所以cos∠ABC===,
在△ABD中,AD2=AB2+BD2-2AB×BD×cos∠ABD=16+-2×4××=,得AD=.
PAGE
7
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.在△ABC中,已知a=2,则bcosC+ccosB等于(
)
A.1
B.
C.2
D.4
2.已知△ABC中,c=6,a=4,B=120°,则b等于(
)
A.76
B.2
C.27
D.2
3.在△ABC中,A=60°,b=1,S△ABC=
,则=(
)
A.
B.
C.
D.2
4.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,设向量p=(a+c,b),q=(b-a,c-a).若p∥q,则角C的大小为(
)
A.
B.
C.
D.
5.在△ABC中,A=60°,AC=16,面积S=220,则BC的长为(
)
A.20
B.75
C.51
D.49
6.在锐角△ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于(
)
A.
B.
C.
D.
7.若==,则△ABC是(
)
A.等边三角形
B.有一内角是30°的直角三角形
C.等腰直角三角形
D.有一内角是30°的等腰三角形
8.设a,b,c为△ABC的三边,且关于x的方程(a2+bc)x2+2x+1=0有两个相等的实数根,则A的度数是(
)
A.120°
B.90°
C.60°
D.30°
9.在锐角三角形ABC中,已知A=2C,则的范围是(
)
A.(0,2)
B.(,2)
C.(,)
D.(,2)
10.在△ABC中,已知BC=5,外接圆半径为5.若·=,则△ABC的周长为(
)
A.11
B.9
C.7
D.5
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,且b=3,c=1,A=2B,则a=(
)
A.4
B.3
C.2
D.2
12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20
n
mile,随后货轮按北偏西30°的方向航行30
min后,又测得灯塔在货轮的东北方向,则货轮的速度为(
)
A.20(+)n
mile/h
B.20(-)n
mile/h
C.20(+)n
mile/h
D.20(-)n
mile/h
二、填空题(本大题共4小题,每小题5分,共20分,请把答案填写在题中横线上)
13.在△ABC中,AC=,A=45°,C=75°,则BC的长为(
)
14.在△ABC中,三个内角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC的值为(
).
15.在△ABC中,若S△ABC=12,ac=48,c-a=2,则b=(
).
16.在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为3-,则∠BAC=(
).
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)·(a-b+c)=ac.
(1)求B;
(2)若sinAsinC=,求C.
18.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
19.(本小题12分)
如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(1)求cos∠CAD的值;
(2)若cos∠BAD=-,sin∠CBA=,求BC的长.
20.(本小题12分)在△ABC中,B=45°,AC=,cosC=.
(1)求BC边的长;
(2)求AB边上的中线CD的长.
21.(本小题12分)如图,有一直径为8
m的半圆形空地,现计划种植甲、乙两种果树,已知单位面积种植甲种果树的经济价值是种植乙种果树经济价值的5倍,但种植甲果树需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲果树生长的需要,该光源照射范围是∠ECF=,点E,F在直径AB上,且∠ABC=.
(1)若CE=
m,求AE的长;
(2)设∠ACE=α,求该空地产生最大经济价值时种植甲种果树的面积.
22.(本小题12分)在△ABC中,AD是BC边的中线,AB2+AC2+AB×AC=BC2,且△ABC的面积为.
(1)求∠BAC的大小及·的值;
(2)若AB=4,求AD的长.
第二章单元质量评估(一)(答案版)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.在△ABC中,已知a=2,则bcosC+ccosB等于( C )
A.1
B.
C.2
D.4
解析:由余弦定理,得bcosC+ccosB=b·+c·==a=2.
2.已知△ABC中,c=6,a=4,B=120°,则b等于( B )
A.76
B.2
C.27
D.2
解析:由余弦定理,得b2=a2+c2-2accosB=76,所以b=2.
3.在△ABC中,A=60°,b=1,S△ABC=
,则=( B )
A.
B.
C.
D.2
解析:依题意得S△ABC=bcsin60°=,得c=4,由余弦定理得a==,由正弦定理得===.
4.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,设向量p=(a+c,b),q=(b-a,c-a).若p∥q,则角C的大小为( B )
A.
B.
C.
D.
解析:∵p∥q,∴(a+c)(c-a)-b(b-a)=0,即a2+b2-c2=ab,∴cosC===,∴C=.
5.在△ABC中,A=60°,AC=16,面积S=220,则BC的长为( D )
A.20
B.75
C.51
D.49
解析:因为S=AC·ABsinA=×16×AB×sin60°=4AB=220,所以AB=55.再用余弦定理求得BC=49.
6.在锐角△ABC中,角A,B所对的边长分别为a,b.若2asinB=b,则角A等于( D )
A.
B.
C.
D.
解析:由已知及正弦定理得2sinAsinB=sinB,因为sinB>0,所以sinA=.又A∈,所以A=.
7.若==,则△ABC是( C )
A.等边三角形
B.有一内角是30°的直角三角形
C.等腰直角三角形
D.有一内角是30°的等腰三角形
解析:∵=,∴acosB=bsinA,∴2RsinAcosB=2RsinBsinA,
又2RsinA≠0,∴cosB=sinB,∴B=45°.同理C=45°,故A=90°.
8.设a,b,c为△ABC的三边,且关于x的方程(a2+bc)x2+2x+1=0有两个相等的实数根,则A的度数是( C )
A.120°
B.90°
C.60°
D.30°
解析:∵由题意可知题中方程的判别式Δ=4(b2+c2)-4(a2+bc)=0,∴b2+c2-a2=bc,cosA=.
又∵0°
A.(0,2)
B.(,2)
C.(,)
D.(,2)
解析:===2cosC,又A+B+C=π,A=2C,∴
A.11
B.9
C.7
D.5
解析:设角A,B,C的对边分别为a,b,c.由题意,得=2×5,∴sinA=,∴A=60°或120°.∵·=,∴A=60°,bccos60°=,∴bc=11.∵a2=b2+c2-bc=(b+c)2-3bc=75,∴(b+c)2=108,∴a+b+c=5+6=11.
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,且b=3,c=1,A=2B,则a=( D )
A.4
B.3
C.2
D.2
解析:∵A=2B,∴C=π-(A+B)=π-3B,sinC=sin3B.由正弦定理知==,∴sinB=3sin3B ①,∵sin3B=sin(2B+B)=sin2BcosB+cos2BsinB=2sinBcos2B+(1-2sin2B)sinB=2sinB-2sin3B+sinB-2sin3B=3sinB-4sin3B ②.把②代入①,得sinB=3(3sinB-4sin3B).分析知B∈,∴sinB≠0,∴sinB=,cosB=,∴由=,得a=6cosB=2.
12.如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20
n
mile,随后货轮按北偏西30°的方向航行30
min后,又测得灯塔在货轮的东北方向,则货轮的速度为( B )
A.20(+)n
mile/h
B.20(-)n
mile/h
C.20(+)n
mile/h
D.20(-)n
mile/h
解析:由题意可知∠SMN=15°+30°=45°,MS=20,∠MNS=45°+(90°-30°)=105°,
∴∠MSN=180°-105°-45°=30°,
设货轮每小时航行x
n
mile,则MN=x,由正弦定理,得=,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=,∴x=20(-),故选B.
二、填空题(本大题共4小题,每小题5分,共20分,请把答案填写在题中横线上)
13.在△ABC中,AC=,A=45°,C=75°,则BC的长为.
解析:由A=45°,C=75°,知B=60°.由正弦定理,得=,所以BC=·AC=×=.
14.在△ABC中,三个内角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC的值为.
解析:在△ABC中,由余弦定理,得cosA=,∴bccosA=,
同理accosB=,abcosC=,∴原式==.
15.在△ABC中,若S△ABC=12,ac=48,c-a=2,则b=2或2.
解析:由S△ABC=acsinB得sinB=,∴B=60°或120°.
由余弦定理得b2=a2+c2-2accosB=(a-c)2+2ac-2accosB=22+2×48-2×48cosB,
∴b2=52或148,即b=2或2.
16.在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为3-,则∠BAC=60°.
解析:∵∠ADB=120°,∴∠ADC=60°,又S△ADC=×AD×DC×sin∠ADC=×2×DC×=DC=3-,∴DC=2-2.∵BD=DC,∴BD=-1,得BC=3-3.在△ABD中,由余弦定理,得AB2=AD2+BD2-2AD·BD·cos120°=4+3-2+1+4(-1)×=6,在△ACD中,由余弦定理,得AC2=AD2+DC2-2AD·DC·cos60°=4+12-8+4-8(-1)×=24-12,在△ABC中,由余弦定理,得cos∠BAC====,∴∠BAC=60°.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)·(a-b+c)=ac.
(1)求B;
(2)若sinAsinC=,求C.
解:(1)因为(a+b+c)(a-b+c)=ac,所以a2+c2-b2=-ac.
由余弦定理得cosB==-,因此B=120°.
(2)由(1)知A+C=60°,所以cos(A-C)=cosAcosC+sinAsinC=cosAcosC-sinAsinC+2sinAsinC=cos(A+C)+2sinAsinC=+2×=,故A-C=30°或A-C=-30°,因此C=15°或C=45°.
18.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
解:(1)证明:由已知得sinB(sinAcosC+cosAsinC)=sinAsinC,∴sinBsin(A+C)=sinAsinC,
则sin2B=sinAsinC,再由正弦定理,可得b2=ac,∴a,b,c成等比数列.
(2)若a=1,c=2,则b2=ac=2,∴cosB==,∴sinB==,
∴△ABC的面积S=acsinB=×1×2×=.
19.(本小题12分)
如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(1)求cos∠CAD的值;
(2)若cos∠BAD=-,sin∠CBA=,求BC的长.
解:(1)在△ADC中,由余弦定理,得cos∠CAD=.
故由题设知,cos∠CAD==.
(2)设∠BAC=α,则α=∠BAD-∠CAD.
因为cos∠CAD=,cos∠BAD=-,
所以sin∠CAD===,sin∠BAD===.
于是sinα=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=×-×=.
在△ABC中,由正弦定理,=.故BC===3.
20.(本小题12分)在△ABC中,B=45°,AC=,cosC=.
(1)求BC边的长;
(2)求AB边上的中线CD的长.
解:(1)由cosC=,得sinC=,sinA=sin(180°-45°-C)=sin(135°-C)=(cosC+sinC)=.
由正弦定理,得BC=·sinA=×=3.
(2)由正弦定理,得AB=·sinC=×=2.BD=AB=1.
由余弦定理,得CD==
=.
21.(本小题12分)如图,有一直径为8
m的半圆形空地,现计划种植甲、乙两种果树,已知单位面积种植甲种果树的经济价值是种植乙种果树经济价值的5倍,但种植甲果树需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲果树生长的需要,该光源照射范围是∠ECF=,点E,F在直径AB上,且∠ABC=.
(1)若CE=
m,求AE的长;
(2)设∠ACE=α,求该空地产生最大经济价值时种植甲种果树的面积.
解:(1)由已知,点C在以AB为直径的半圆周上,所以△ACB为直角三角形,
因为AB=8,∠ABC=,所以∠A=,AC=4,
在△ACE中,CE2=AC2+AE2-2AC×AEcos∠A,且CE=,所以13=16+AE2-4AE,
解得AE=1或AE=3.
(2)因为∠ACB=,∠ECF=,所以∠ACE=α∈,
所以∠AFC=π-∠A-∠ACF=π--=-α,
在△ACF中,===.
所以CF=.
在△ACE中,==,
所以CE=.
若要产生最大经济价值,则△ECF的面积最大.
S△ECF=CE×CFsin∠ECF==,
因为α∈,所以0≤sin≤1,
所以当α=时,S△ECF取得最大值,为4
m2,即种植甲种果树的面积为4
m2时,该空地产生的经济价值最大.
22.(本小题12分)在△ABC中,AD是BC边的中线,AB2+AC2+AB×AC=BC2,且△ABC的面积为.
(1)求∠BAC的大小及·的值;
(2)若AB=4,求AD的长.
解:(1)在△ABC中,由AB2+AC2+AB×AC=BC2,可得=-=cos∠BAC,故∠BAC=120°.
因为S△ABC=AB×AC×sin∠BAC=×AB×AC×sin120°=,
即×AB×AC×=,所以AB×AC=4.
所以·=||×||×cos120°=||×||×=4×=-2.
(2)由AB=4,AB×AC=4,得AC=1.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB×AC×cos∠BAC=16+1-2×4×1×=21,
即BC=,
所以cos∠ABC===,
在△ABD中,AD2=AB2+BD2-2AB×BD×cos∠ABD=16+-2×4××=,得AD=.
PAGE
7
