13.1.1轴对称-人教版八年级数学上册导学案(含答案)
文档属性
| 名称 | 13.1.1轴对称-人教版八年级数学上册导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 10:51:33 | ||
图片预览

文档简介
13.1.1轴对称
备课时间:
授课时间:
年
班
学习目标:
1、知识与技能:
在生活实例中认识轴对称图形;分析轴对称图形,理解轴对称图形的概念,培养说理和进行简单推理的能力.
2、过程与方法:
经历观察、推理、归纳等探索过程,体验并掌握探索、归纳图形性质的推理方法.
3、情感态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:理解轴对称图形的概念.
学习难点:
能够识别轴对称图形并找出它的对称轴.
学习过程:
一、自主学习
知识点一:
1、观察课本几副图片,你能找出它们的共同特征吗?
2、你能列举出一些现实生活中具有这种特征的物体吗?
3、如果一个平面图形沿一条_____折叠,_____两旁的部分能够互相_____,这个图形就叫做轴对称图形,这条____就是它的对称轴,这时,我们也说这个图形关于这条____(成轴)
对称.
试一试:1.下面的图形是轴对称图形吗?如果是,指出对称轴。
知识点二:
1.观察课本59页的三幅图形,并沿虚线折叠,每对图形有什么共同特征?
2、一个图形沿着某条直线折叠,如果他能够与________重合,那么就说这两个图形关于这条直线对称,这条直线叫做_______,折叠后________叫做对称点.
3、成轴对称的两个图形全等吗?
4、全等的两个图形成轴对称吗?试举例说明。(可以画图说明)
二、合作探究、交流展示:
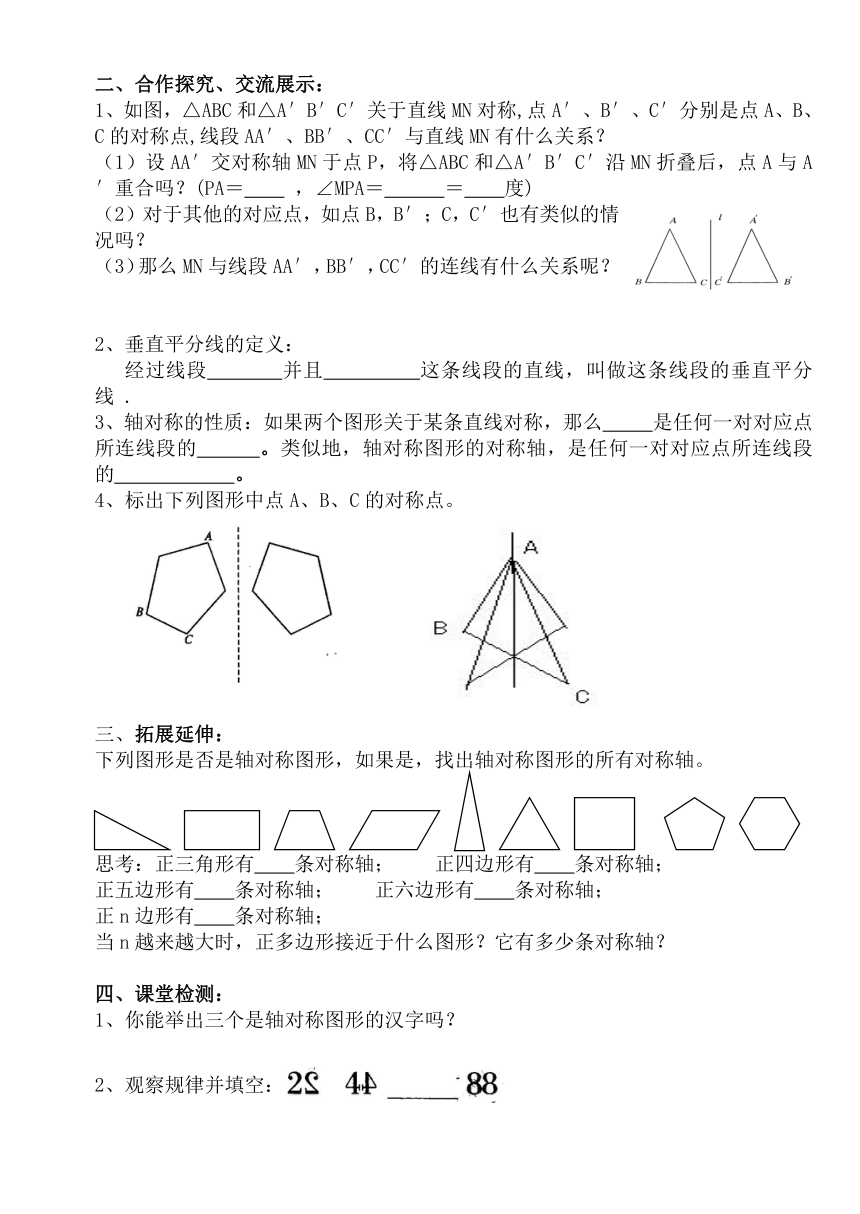
1、如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
(1)设AA′交对称轴MN于点P,将△ABC和△A′B′C′沿MN折叠后,点A与A′重合吗?(PA=
,∠MPA=
=
度)
(2)对于其他的对应点,如点B,B′;C,C′也有类似的情况吗?
(3)那么MN与线段AA′,BB′,CC′的连线有什么关系呢?
2、垂直平分线的定义:
经过线段
并且
这条线段的直线,叫做这条线段的垂直平分线
.
3、轴对称的性质:如果两个图形关于某条直线对称,那么
是任何一对对应点所连线段的
。类似地,轴对称图形的对称轴,是任何一对对应点所连线段的
。
4、标出下列图形中点A、B、C的对称点。
三、拓展延伸:
下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
思考:正三角形有 条对称轴;
正四边形有 条对称轴;
正五边形有 条对称轴;
正六边形有 条对称轴;
正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
四、课堂检测:
1、你能举出三个是轴对称图形的汉字吗?
2、观察规律并填空:
3、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
4、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
5、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是
,线段AD、AB的对应线段分别是
,CD=
,∠CBA=
,∠ADC=
.
(2)AE与BF平行吗?为什么?
(3)AE与BF平行,能说明轴对称图形对称点的连线一定互相平行吗?
(4)延长线段BC、FG,交于点P,延长线段AB、EF,交于点Q,,你有什么发现吗?
五、学(教)后反思:
收获:
不足:
答案
一、自主学习
知识点一:1、2、略
3、直线;直线;重合;直线;直线
知识点二:1、略
2、另一个图形;对称轴;重合的点;
3、成轴对称的两个图形全等吗?
解:成轴对称的两个图形是全等的.因为轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,
又∵能够完全重合的两个图形是全等形,
∴成轴对称的两个图形是全等的.
4、不一定
图略
二、合作探究、交流展示:
1、AA′⊥MN;BB′⊥MN;CC′⊥MN
(1)重合;PA=PA′;∠MPA=∠MPA′=90°
(2)PB=PB′;∠MPB=∠MPB′=90°;PC=PC′;∠MPC=∠MPC′=90°
(3)AA′⊥MN;BB′⊥MN;CC′⊥MN
2、中点;垂直;
3、对称轴;垂直平分线;垂直平分线
4、略
三、拓展延伸:
思考:3;4;5;6;n;圆形;无数条
四、课堂检测:
1、王、中、田等
2、
3、区别:
(1)轴对称是指两个图形间的位置关系,轴对称图形是指一个具有特殊形状的图形;
(2)轴对称涉及两个图形,轴对称图形是对一个图形而言的。
联系:
(1)定义中都有一条直线,都要沿着这条直线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。
4、略
5、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)E、F、G、H;EH、EF;GH;∠GFE;∠EHG
(2)平行,因为每对对应点连接成的线段被对称轴垂直平分,即EA⊥MN,BF⊥MN,所以AE∥BF
(3)不能,因为轴对称图形对称点的连线是重合或互相平行;
(4)发现:对称线段所在直线相交,那么这个交点一定在对称轴上.
备课时间:
授课时间:
年
班
学习目标:
1、知识与技能:
在生活实例中认识轴对称图形;分析轴对称图形,理解轴对称图形的概念,培养说理和进行简单推理的能力.
2、过程与方法:
经历观察、推理、归纳等探索过程,体验并掌握探索、归纳图形性质的推理方法.
3、情感态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:理解轴对称图形的概念.
学习难点:
能够识别轴对称图形并找出它的对称轴.
学习过程:
一、自主学习
知识点一:
1、观察课本几副图片,你能找出它们的共同特征吗?
2、你能列举出一些现实生活中具有这种特征的物体吗?
3、如果一个平面图形沿一条_____折叠,_____两旁的部分能够互相_____,这个图形就叫做轴对称图形,这条____就是它的对称轴,这时,我们也说这个图形关于这条____(成轴)
对称.
试一试:1.下面的图形是轴对称图形吗?如果是,指出对称轴。
知识点二:
1.观察课本59页的三幅图形,并沿虚线折叠,每对图形有什么共同特征?
2、一个图形沿着某条直线折叠,如果他能够与________重合,那么就说这两个图形关于这条直线对称,这条直线叫做_______,折叠后________叫做对称点.
3、成轴对称的两个图形全等吗?
4、全等的两个图形成轴对称吗?试举例说明。(可以画图说明)
二、合作探究、交流展示:
1、如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
(1)设AA′交对称轴MN于点P,将△ABC和△A′B′C′沿MN折叠后,点A与A′重合吗?(PA=
,∠MPA=
=
度)
(2)对于其他的对应点,如点B,B′;C,C′也有类似的情况吗?
(3)那么MN与线段AA′,BB′,CC′的连线有什么关系呢?
2、垂直平分线的定义:
经过线段
并且
这条线段的直线,叫做这条线段的垂直平分线
.
3、轴对称的性质:如果两个图形关于某条直线对称,那么
是任何一对对应点所连线段的
。类似地,轴对称图形的对称轴,是任何一对对应点所连线段的
。
4、标出下列图形中点A、B、C的对称点。
三、拓展延伸:
下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
思考:正三角形有 条对称轴;
正四边形有 条对称轴;
正五边形有 条对称轴;
正六边形有 条对称轴;
正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
四、课堂检测:
1、你能举出三个是轴对称图形的汉字吗?
2、观察规律并填空:
3、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
4、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
5、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是
,线段AD、AB的对应线段分别是
,CD=
,∠CBA=
,∠ADC=
.
(2)AE与BF平行吗?为什么?
(3)AE与BF平行,能说明轴对称图形对称点的连线一定互相平行吗?
(4)延长线段BC、FG,交于点P,延长线段AB、EF,交于点Q,,你有什么发现吗?
五、学(教)后反思:
收获:
不足:
答案
一、自主学习
知识点一:1、2、略
3、直线;直线;重合;直线;直线
知识点二:1、略
2、另一个图形;对称轴;重合的点;
3、成轴对称的两个图形全等吗?
解:成轴对称的两个图形是全等的.因为轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,
又∵能够完全重合的两个图形是全等形,
∴成轴对称的两个图形是全等的.
4、不一定
图略
二、合作探究、交流展示:
1、AA′⊥MN;BB′⊥MN;CC′⊥MN
(1)重合;PA=PA′;∠MPA=∠MPA′=90°
(2)PB=PB′;∠MPB=∠MPB′=90°;PC=PC′;∠MPC=∠MPC′=90°
(3)AA′⊥MN;BB′⊥MN;CC′⊥MN
2、中点;垂直;
3、对称轴;垂直平分线;垂直平分线
4、略
三、拓展延伸:
思考:3;4;5;6;n;圆形;无数条
四、课堂检测:
1、王、中、田等
2、
3、区别:
(1)轴对称是指两个图形间的位置关系,轴对称图形是指一个具有特殊形状的图形;
(2)轴对称涉及两个图形,轴对称图形是对一个图形而言的。
联系:
(1)定义中都有一条直线,都要沿着这条直线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。
4、略
5、如图,四边形ABCD与四边形EFGH关于MN对称。
(1)E、F、G、H;EH、EF;GH;∠GFE;∠EHG
(2)平行,因为每对对应点连接成的线段被对称轴垂直平分,即EA⊥MN,BF⊥MN,所以AE∥BF
(3)不能,因为轴对称图形对称点的连线是重合或互相平行;
(4)发现:对称线段所在直线相交,那么这个交点一定在对称轴上.
