25.2.2用树状图法求概率-人教版九年级数学上册练习(Word版 含解析)
文档属性
| 名称 | 25.2.2用树状图法求概率-人教版九年级数学上册练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 255.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 14:04:22 | ||
图片预览



文档简介
人教版九年级数学上册25.2.2用树状图法求概率
一.选择题(共6小题)
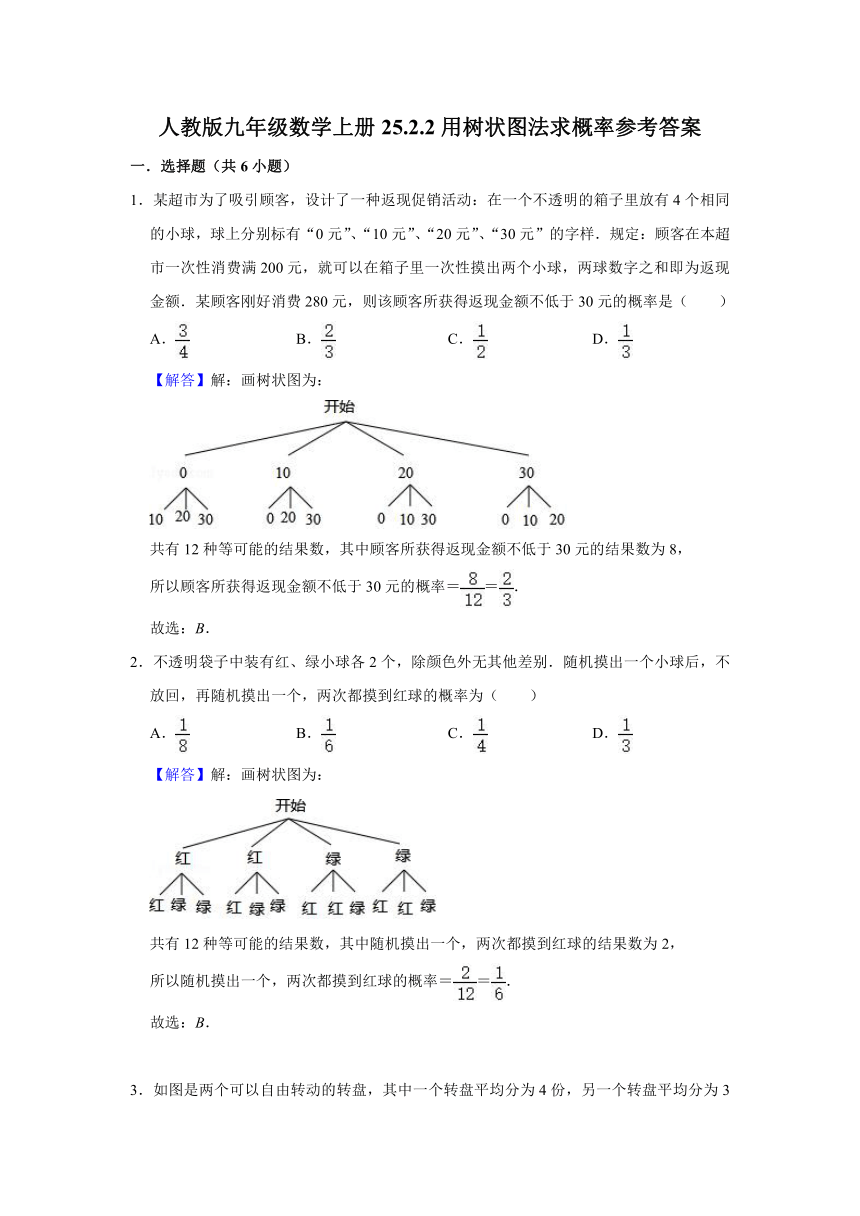
1.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和即为返现金额.某顾客刚好消费280元,则该顾客所获得返现金额不低于30元的概率是( )
A.
B.
C.
D.
2.不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( )
A.
B.
C.
D.
3.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
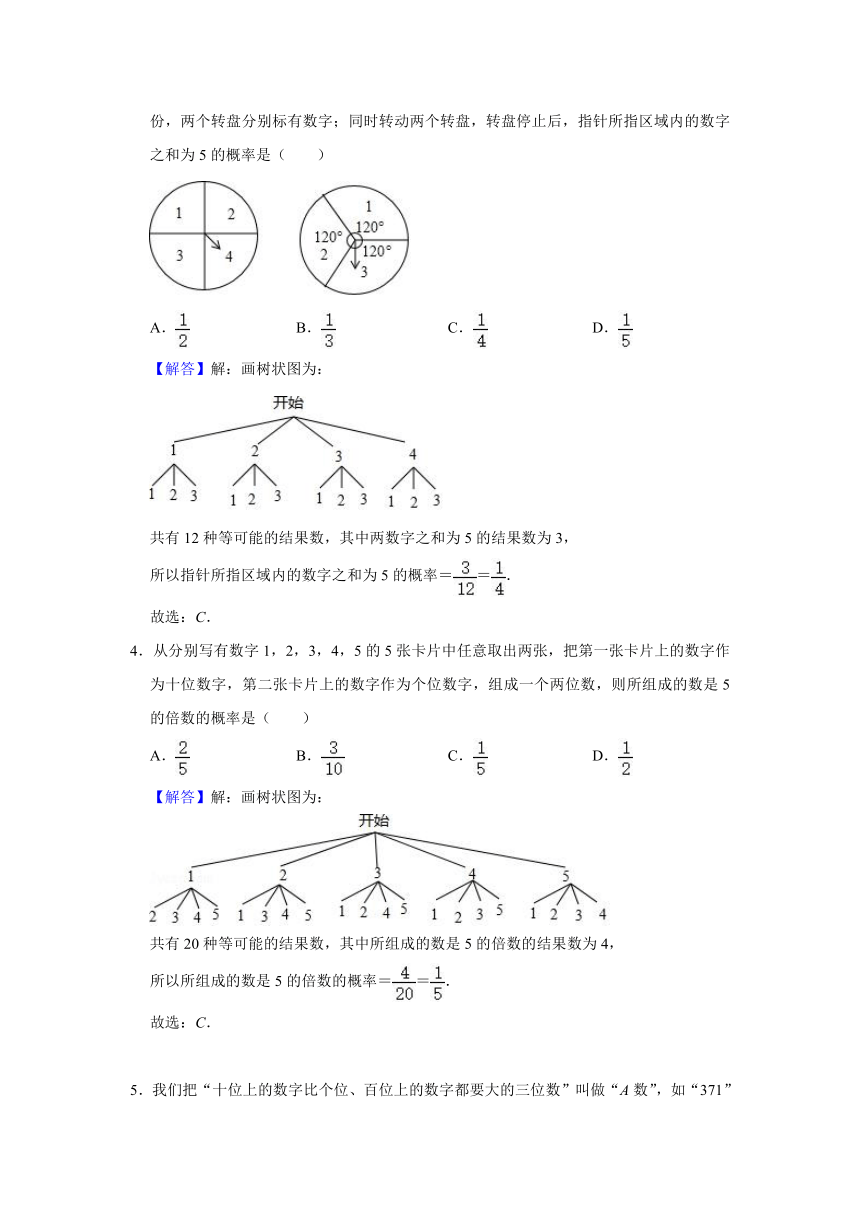
4.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
5.我们把“十位上的数字比个位、百位上的数字都要大的三位数”叫做“A数”,如“371”就是一个“A数”.若十位上的数字为4,则从1,2,3,5中任取两个不同的数,能与4组成“A数”的概率为( )
A.
B.
C.
D.
6.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
二.填空题(共6小题)
7.只有1和它本身两个因数且大于1的正整数叫做素数.从7、11、19、23这4个素数中随机抽取2个数,抽到的2个素数之和等于30的概率为
.
8.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是
.
9.现有三张分别标有数字2,3,4的卡片;它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a;将卡片放回后,再次任意抽取一张,将上面的数字记为b,则点(a,b)
在直线y=x+1图象上的概率为
.
10.下个月学校将为片区学校展示“音乐、体育、美术”兴趣活动观摩.小明、小丽随机从三个场所选择一个担任志愿者服务,两人恰好选择同一场所的概率是
.
11.疫情期间,某小区卡点有6名志愿者,其中4名女志愿者,2名男志愿者,若随机抽取2人为组长,恰好抽到2名男志愿者的概率为
.
12.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心神领会”,据此规则两人“心神领会”的概率是
.
三.解答题(共3小题)
13.随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.
(1)李老师被分配到“洗手监督岗”的概率为
;
(2)用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.
14.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是
;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
15.甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.
(1)若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是
.
(2)若从支援的4名医护人员中分别随机选2名,用画树状图或列表的方法求出这两名医护人员来自不同医院的概率.
人教版九年级数学上册25.2.2用树状图法求概率参考答案
一.选择题(共6小题)
1.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和即为返现金额.某顾客刚好消费280元,则该顾客所获得返现金额不低于30元的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中顾客所获得返现金额不低于30元的结果数为8,
所以顾客所获得返现金额不低于30元的概率==.
故选:B.
2.不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中随机摸出一个,两次都摸到红球的结果数为2,
所以随机摸出一个,两次都摸到红球的概率==.
故选:B.
3.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中两数字之和为5的结果数为3,
所以指针所指区域内的数字之和为5的概率==.
故选:C.
4.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有20种等可能的结果数,其中所组成的数是5的倍数的结果数为4,
所以所组成的数是5的倍数的概率==.
故选:C.
5.我们把“十位上的数字比个位、百位上的数字都要大的三位数”叫做“A数”,如“371”就是一个“A数”.若十位上的数字为4,则从1,2,3,5中任取两个不同的数,能与4组成“A数”的概率为( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中能与4组成“A数”的结果数为6,
所以能与4组成“A数”的概率==.
故选:C.
6.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
【解答】解:根据题意,画树状图如下:
共有20种等可能的结果数,其中两次摸出小球的标号之和能被3整除的占8种,
所有两次摸出小球的标号之和能被3整除的概率==.
故选:B.
二.填空题(共6小题)
7.只有1和它本身两个因数且大于1的正整数叫做素数.从7、11、19、23这4个素数中随机抽取2个数,抽到的2个素数之和等于30的概率为 .
【解答】解:画树状图为:
共有12种等可能的结果,抽到的2个素数之和等于30的结果数为4,
所以抽到的2个素数之和等于30的概率==.
故答案为.
8.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是 .
【解答】解:画树状图为:
共有4种等可能的结果,其中两次都摸到相同颜色的小球的结果数为2,
所以两次都摸到相同颜色的小球的概率==.
故答案为.
9.现有三张分别标有数字2,3,4的卡片;它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a;将卡片放回后,再次任意抽取一张,将上面的数字记为b,则点(a,b)
在直线y=x+1图象上的概率为 .
【解答】解:画树状图为:
共有9种等可能的结果,其中点(a,b)
在直线y=x+1图象上的结果为(2,2),(4,3),
所以点(a,b)
在直线y=x+1图象上的概率=.
故答案为.
10.下个月学校将为片区学校展示“音乐、体育、美术”兴趣活动观摩.小明、小丽随机从三个场所选择一个担任志愿者服务,两人恰好选择同一场所的概率是 .
【解答】解:画树状图为:
共有9种等可能的结果数,其中两人恰好选择同一场所的结果数为3,
所以两人恰好选择同一场所的概率==.
11.疫情期间,某小区卡点有6名志愿者,其中4名女志愿者,2名男志愿者,若随机抽取2人为组长,恰好抽到2名男志愿者的概率为 .
【解答】解:画树状图为:
共有30种等可能的结果数,其中抽到2名男志愿者的结果数为2,
所以抽到2名男志愿者的概率==.
故答案为.
12.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心神领会”,据此规则两人“心神领会”的概率是 .
【解答】解:画树状图为:
共有16种等可能的结果数,其中满足|m﹣n|≤1的结果数为10,
所以两人“心神领会”的概率==.
故答案为.
三.解答题(共3小题)
13.随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.
(1)李老师被分配到“洗手监督岗”的概率为 ;
(2)用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.
【解答】解:(1)李老师被分配到“洗手监督岗”的概率=;
故答案为:;
(2)画树状图为:
共有16种等可能的结果,其中李老师和王老师被分配到同一个监督岗的结果数为4,
所以李老师和王老师被分配到同一个监督岗的概率==.
14.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是 ;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
【解答】解:(1)在“2”中已选择了地理,从剩下的化学、生物,思想品德三科中选一科,因此选择生物的概率为;
故答案为:;
(2)用树状图表示所有可能出现的结果如下:
共有12种可能出现的结果,其中选中“化学”“生物”的有2种,
∴P(化学生物)==.
15.甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.
(1)若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是 .
(2)若从支援的4名医护人员中分别随机选2名,用画树状图或列表的方法求出这两名医护人员来自不同医院的概率.
【解答】解:(1)从这4名医护人员中随机选1名,选中的是男医护人员的概率==;
故答案为;
(2)画树状图为:(a、b表示甲医院的男女医护人员,c、d表示乙医院的男女医护人员)
共有12种等可能的结果数,其中这两名医护人员来自不同医院的结果数为8,
所以这两名医护人员来自不同医院的概率==.
一.选择题(共6小题)
1.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和即为返现金额.某顾客刚好消费280元,则该顾客所获得返现金额不低于30元的概率是( )
A.
B.
C.
D.
2.不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( )
A.
B.
C.
D.
3.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
4.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
5.我们把“十位上的数字比个位、百位上的数字都要大的三位数”叫做“A数”,如“371”就是一个“A数”.若十位上的数字为4,则从1,2,3,5中任取两个不同的数,能与4组成“A数”的概率为( )
A.
B.
C.
D.
6.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
二.填空题(共6小题)
7.只有1和它本身两个因数且大于1的正整数叫做素数.从7、11、19、23这4个素数中随机抽取2个数,抽到的2个素数之和等于30的概率为
.
8.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是
.
9.现有三张分别标有数字2,3,4的卡片;它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a;将卡片放回后,再次任意抽取一张,将上面的数字记为b,则点(a,b)
在直线y=x+1图象上的概率为
.
10.下个月学校将为片区学校展示“音乐、体育、美术”兴趣活动观摩.小明、小丽随机从三个场所选择一个担任志愿者服务,两人恰好选择同一场所的概率是
.
11.疫情期间,某小区卡点有6名志愿者,其中4名女志愿者,2名男志愿者,若随机抽取2人为组长,恰好抽到2名男志愿者的概率为
.
12.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心神领会”,据此规则两人“心神领会”的概率是
.
三.解答题(共3小题)
13.随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.
(1)李老师被分配到“洗手监督岗”的概率为
;
(2)用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.
14.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是
;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
15.甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.
(1)若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是
.
(2)若从支援的4名医护人员中分别随机选2名,用画树状图或列表的方法求出这两名医护人员来自不同医院的概率.
人教版九年级数学上册25.2.2用树状图法求概率参考答案
一.选择题(共6小题)
1.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和即为返现金额.某顾客刚好消费280元,则该顾客所获得返现金额不低于30元的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中顾客所获得返现金额不低于30元的结果数为8,
所以顾客所获得返现金额不低于30元的概率==.
故选:B.
2.不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个小球后,不放回,再随机摸出一个,两次都摸到红球的概率为( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中随机摸出一个,两次都摸到红球的结果数为2,
所以随机摸出一个,两次都摸到红球的概率==.
故选:B.
3.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中两数字之和为5的结果数为3,
所以指针所指区域内的数字之和为5的概率==.
故选:C.
4.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有20种等可能的结果数,其中所组成的数是5的倍数的结果数为4,
所以所组成的数是5的倍数的概率==.
故选:C.
5.我们把“十位上的数字比个位、百位上的数字都要大的三位数”叫做“A数”,如“371”就是一个“A数”.若十位上的数字为4,则从1,2,3,5中任取两个不同的数,能与4组成“A数”的概率为( )
A.
B.
C.
D.
【解答】解:画树状图为:
共有12种等可能的结果数,其中能与4组成“A数”的结果数为6,
所以能与4组成“A数”的概率==.
故选:C.
6.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
【解答】解:根据题意,画树状图如下:
共有20种等可能的结果数,其中两次摸出小球的标号之和能被3整除的占8种,
所有两次摸出小球的标号之和能被3整除的概率==.
故选:B.
二.填空题(共6小题)
7.只有1和它本身两个因数且大于1的正整数叫做素数.从7、11、19、23这4个素数中随机抽取2个数,抽到的2个素数之和等于30的概率为 .
【解答】解:画树状图为:
共有12种等可能的结果,抽到的2个素数之和等于30的结果数为4,
所以抽到的2个素数之和等于30的概率==.
故答案为.
8.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是 .
【解答】解:画树状图为:
共有4种等可能的结果,其中两次都摸到相同颜色的小球的结果数为2,
所以两次都摸到相同颜色的小球的概率==.
故答案为.
9.现有三张分别标有数字2,3,4的卡片;它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a;将卡片放回后,再次任意抽取一张,将上面的数字记为b,则点(a,b)
在直线y=x+1图象上的概率为 .
【解答】解:画树状图为:
共有9种等可能的结果,其中点(a,b)
在直线y=x+1图象上的结果为(2,2),(4,3),
所以点(a,b)
在直线y=x+1图象上的概率=.
故答案为.
10.下个月学校将为片区学校展示“音乐、体育、美术”兴趣活动观摩.小明、小丽随机从三个场所选择一个担任志愿者服务,两人恰好选择同一场所的概率是 .
【解答】解:画树状图为:
共有9种等可能的结果数,其中两人恰好选择同一场所的结果数为3,
所以两人恰好选择同一场所的概率==.
11.疫情期间,某小区卡点有6名志愿者,其中4名女志愿者,2名男志愿者,若随机抽取2人为组长,恰好抽到2名男志愿者的概率为 .
【解答】解:画树状图为:
共有30种等可能的结果数,其中抽到2名男志愿者的结果数为2,
所以抽到2名男志愿者的概率==.
故答案为.
12.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心神领会”,据此规则两人“心神领会”的概率是 .
【解答】解:画树状图为:
共有16种等可能的结果数,其中满足|m﹣n|≤1的结果数为10,
所以两人“心神领会”的概率==.
故答案为.
三.解答题(共3小题)
13.随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.
(1)李老师被分配到“洗手监督岗”的概率为 ;
(2)用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.
【解答】解:(1)李老师被分配到“洗手监督岗”的概率=;
故答案为:;
(2)画树状图为:
共有16种等可能的结果,其中李老师和王老师被分配到同一个监督岗的结果数为4,
所以李老师和王老师被分配到同一个监督岗的概率==.
14.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是 ;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
【解答】解:(1)在“2”中已选择了地理,从剩下的化学、生物,思想品德三科中选一科,因此选择生物的概率为;
故答案为:;
(2)用树状图表示所有可能出现的结果如下:
共有12种可能出现的结果,其中选中“化学”“生物”的有2种,
∴P(化学生物)==.
15.甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.
(1)若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是 .
(2)若从支援的4名医护人员中分别随机选2名,用画树状图或列表的方法求出这两名医护人员来自不同医院的概率.
【解答】解:(1)从这4名医护人员中随机选1名,选中的是男医护人员的概率==;
故答案为;
(2)画树状图为:(a、b表示甲医院的男女医护人员,c、d表示乙医院的男女医护人员)
共有12种等可能的结果数,其中这两名医护人员来自不同医院的结果数为8,
所以这两名医护人员来自不同医院的概率==.
同课章节目录
