人教版八年级上册 数学《11.3 多边形及其内角和》同步跟踪训练(Word版 含解析)
文档属性
| 名称 | 人教版八年级上册 数学《11.3 多边形及其内角和》同步跟踪训练(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 12:16:16 | ||
图片预览




文档简介
《11.3
多边形及其内角和》同步跟踪训练
一.选择题
1.如果一个n边形的外角和是内角和的一半,那么n的值为( )
A.6
B.7
C.8
D.9
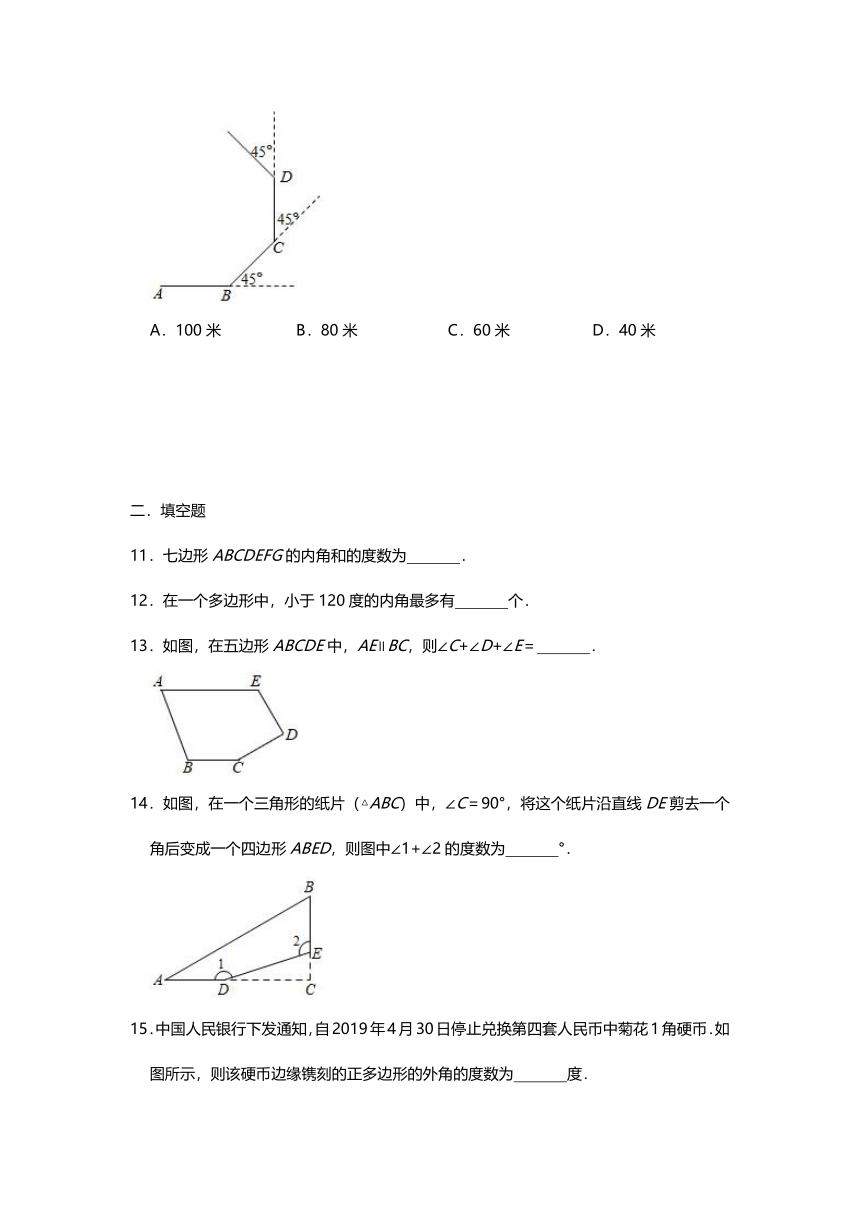
2.如图,五边形ABCDE的每个内角都相等,分别过顶点D、E作一条射线,交点为H,如果CD∥EH,那么∠DEH的度数是( )
A.50°
B.60°
C.72°
D.75°
3.如图,六边形ABCDEF内部有一点G,连结BG、DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为( )
A.60°
B.70°
C.80°
D.90°
4.一个多边形的外角和是内角和的,这个多边形的边数是( )
A.7
B.8
C.9
D.10
5.若一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.六边形
B.八边形
C.十边形
D.十二边形
6.多边形的内角和不可能为( )
A.180°
B.540°
C.1080°
D.1200°
7.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是( )
A.50°
B.55°
C.40°
D.45°
8.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右偏108°方向行走
D.每段直路要长
9.设四边形的内角和等于a,五边形的内角和等于b,则a与b的关系是( )
A.a>b
B.a=b
C.a=b+180°
D.b=a+180°
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
二.填空题
11.七边形ABCDEFG的内角和的度数为
.
12.在一个多边形中,小于120度的内角最多有
个.
13.如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=
.
14.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为
°.
15.中国人民银行下发通知,自2019年4月30日停止兑换第四套人民币中菊花1角硬币.如图所示,则该硬币边缘镌刻的正多边形的外角的度数为
度.
三.解答题
16.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
17.(1)阅读材料并填空:运用平行线及其性质,可以推理证明出很多有用的结论,如图甲,点D是△ABC中BC边延长线上的一点,过点C作CE∥AB,则有如下推理证明:
∵CE∥AB(已知),
∴∠ACE=
(两直线平行,
).
∠ECD=
(两直线平行,
).
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=
(等量代换).
(2)如图乙,根据(1)中的平行线的构造方法,过点D作DE∥AB交BC于点E,运用(1)中的结论,即可推理出四边形ABCD中∠A+∠B+∠C+∠CDA的度数.具体推理步骤如下,请填空:
由(1)知:∠BED=∠C+
.
∵DE∥AB,
∴
+∠ADE=180°(两直线平行,
),
∠B+∠BED=180°(两直线平行,同旁内角互补).
∵∠CDA=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=
°(等量代换).
18.完成下面的证明:
如图,在四个角都是直角的四边形ABCD中,AD∥BC,点E,F分别在边AD,BC上,BE平分∠ABC,DF平分∠ADC,求证:BE∥FD.
证明:∵四边形ABCD的四个角都是直角,
∴∠ABC=∠ADC=
°(直角定义).
∵BE平分∠ABC,DF平分∠ADC,
∴∠EBC=∠ABC=×90°=45°,(角平分线定义),
∴∠EBC=∠ADF.
∵AD∥BC,∴∠ADF=∠DFC(
).
∴∠EBC=∠DFC(等量代换),∴BE∥DF(
).
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
20.阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=
°.
参考答案
一.选择题
1.解:由题意得(n﹣2)?180°×=360°,
解得n=6.
故选:A.
2.解:∵五边形的内角和为:(5﹣2)?180°=540°且每个内角都相等,
∴∠CDE=540°÷5=108°.
∵CD∥EH,
∴∠CDE+∠DEH=180°,
∴∠DEH=180°﹣108°=72°.
故选:C.
3.解:∵多边形ABCDEF是六边形,
∴∠1+∠5+∠4+∠3+∠2+∠6+∠7+∠C=180°×(6﹣2)=720°,
∵∠1+∠2+∠3+∠4+∠5=440°,
∴∠6+∠7+∠C=720°﹣440°=280°,
∵多边形BCDG是四边形,
∴∠C+∠6+∠7+∠G=360°,
∴∠G=360°﹣(∠6+∠7+∠C)=360°﹣280°=80°,
故选:C.
4.解:设这个多边形的边数为n,
依题意得:(n﹣2)180°=360°,
解得n=9,
故选:C.
5.解:设这个多边形的边数为n,依题意得
(n﹣2)?180°=5×360°,
解得n=12,
∴这个多边形是十二边形,
故选:D.
6.解:多边形的内角和可以表示成(n﹣2)?180°(n≥3且n是整数),n应为整数,所以n﹣2也是整数,所以多边形的内角能被180整除,因为在这四个选项中不是180°的倍数的只有1200°.
故选:D.
7.解:∵∠1、∠2、∠3、∠4的外角的角度和为230°,
∴∠1+∠2+∠3+∠4+230°=4×180°,
∴∠1+∠2+∠3+∠4=490°,
∵五边形OAGFE内角和=(5﹣2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°﹣490°=50°,
故选:A.
8.解:∵从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,
∴=72°,
∴每走完一段直路后沿向右偏72°方向行走.
故选:A.
9.解:根据题意可得:a=(4﹣2)×180°,b=(5﹣2)×180°,
∴b=a+180°.
故选:D.
10.解:∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×10=80(m).
故选:B.
二.填空题(共5小题)
11.解:七边形ABCDEFG的内角和的度数为:(7﹣2)×180°=900°.
故答案为:900°.
12.解:∵多边形的内角小于120°,
∴外角大于60°,
∴这个多边形小于120°的内角的个数<360°÷60°=6,
∴在一个多边形中,小于120度的内角最多有5个.
故答案为:5.
13.过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
14.解:∵∠C=90°,
∴∠A+∠B=90°,
∵∠1+∠A+∠B+∠2=360°,
∴∠1+∠2=360°﹣90°=270°,
故答案为:270.
15.解:∵正多边形的外角和是360°,
∴360°÷9=40°.
故答案为:40.
三.解答题(共5小题)
16.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
17.解:(1)如图甲,点D是△ABC中BC边延长线上的一点,
过点C作CE∥AB,则有如下推理证明:
∵CE∥AB(已知),
∴∠ACE=∠A(两直线平行,内错角相等),∠ECD=∠B(两直线平行,同位角相等),
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B(等量代换).
(2)如图乙,根据(1)中的平行线的构造方法,
过点D作DE∥AB交BC于点E,
运用(1)中的结论,即可推理出四边形ABCD中∠A+∠B+∠C+∠CDA的度数.
由(1)知:∠BED=∠C+∠CDE.
∵DE∥AB,
∴∠A+∠ADE=180°(两直线平行,同旁内角互补),∠B+∠BED=180°(两直线平行,同旁内角互补).
∵∠CD4=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=360°(等量代换)
故答案为:(1)∠A;内错角相等;∠B;同位角相等;∠A+∠B;(2)∠CDE;∠A;同旁内角互补;360.
18.证明:∵四边形ABCD的四个角都是直角,
∴∠ABC=∠ADC=90°
(
直角定义
).
∵BE平分∠ABC,DF
平分∠ADC,
∴∠EBC=∠ABC=×90°=45°,∠ADF=∠ADC=×90°=45°,
∴∠EBC=∠ADF,
∵AD∥BC,
∴∠ADF=∠DFC(两直线平行,内错角相等).
∴∠EBC=∠DFC(等量代换),
∴BE∥DF(同位角相等,两直线平行).
故答案为:90;两直线平行,内错角相等;同位角相等,两直线平行.
19.解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
20.解:(2)延长BC交AD于点M
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(3)如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β.
由(2)可知,,
解得x=64°
故答案为64.
多边形及其内角和》同步跟踪训练
一.选择题
1.如果一个n边形的外角和是内角和的一半,那么n的值为( )
A.6
B.7
C.8
D.9
2.如图,五边形ABCDE的每个内角都相等,分别过顶点D、E作一条射线,交点为H,如果CD∥EH,那么∠DEH的度数是( )
A.50°
B.60°
C.72°
D.75°
3.如图,六边形ABCDEF内部有一点G,连结BG、DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为( )
A.60°
B.70°
C.80°
D.90°
4.一个多边形的外角和是内角和的,这个多边形的边数是( )
A.7
B.8
C.9
D.10
5.若一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.六边形
B.八边形
C.十边形
D.十二边形
6.多边形的内角和不可能为( )
A.180°
B.540°
C.1080°
D.1200°
7.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是( )
A.50°
B.55°
C.40°
D.45°
8.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右偏108°方向行走
D.每段直路要长
9.设四边形的内角和等于a,五边形的内角和等于b,则a与b的关系是( )
A.a>b
B.a=b
C.a=b+180°
D.b=a+180°
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
二.填空题
11.七边形ABCDEFG的内角和的度数为
.
12.在一个多边形中,小于120度的内角最多有
个.
13.如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=
.
14.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为
°.
15.中国人民银行下发通知,自2019年4月30日停止兑换第四套人民币中菊花1角硬币.如图所示,则该硬币边缘镌刻的正多边形的外角的度数为
度.
三.解答题
16.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
17.(1)阅读材料并填空:运用平行线及其性质,可以推理证明出很多有用的结论,如图甲,点D是△ABC中BC边延长线上的一点,过点C作CE∥AB,则有如下推理证明:
∵CE∥AB(已知),
∴∠ACE=
(两直线平行,
).
∠ECD=
(两直线平行,
).
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=
(等量代换).
(2)如图乙,根据(1)中的平行线的构造方法,过点D作DE∥AB交BC于点E,运用(1)中的结论,即可推理出四边形ABCD中∠A+∠B+∠C+∠CDA的度数.具体推理步骤如下,请填空:
由(1)知:∠BED=∠C+
.
∵DE∥AB,
∴
+∠ADE=180°(两直线平行,
),
∠B+∠BED=180°(两直线平行,同旁内角互补).
∵∠CDA=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=
°(等量代换).
18.完成下面的证明:
如图,在四个角都是直角的四边形ABCD中,AD∥BC,点E,F分别在边AD,BC上,BE平分∠ABC,DF平分∠ADC,求证:BE∥FD.
证明:∵四边形ABCD的四个角都是直角,
∴∠ABC=∠ADC=
°(直角定义).
∵BE平分∠ABC,DF平分∠ADC,
∴∠EBC=∠ABC=×90°=45°,(角平分线定义),
∴∠EBC=∠ADF.
∵AD∥BC,∴∠ADF=∠DFC(
).
∴∠EBC=∠DFC(等量代换),∴BE∥DF(
).
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
20.阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=
°.
参考答案
一.选择题
1.解:由题意得(n﹣2)?180°×=360°,
解得n=6.
故选:A.
2.解:∵五边形的内角和为:(5﹣2)?180°=540°且每个内角都相等,
∴∠CDE=540°÷5=108°.
∵CD∥EH,
∴∠CDE+∠DEH=180°,
∴∠DEH=180°﹣108°=72°.
故选:C.
3.解:∵多边形ABCDEF是六边形,
∴∠1+∠5+∠4+∠3+∠2+∠6+∠7+∠C=180°×(6﹣2)=720°,
∵∠1+∠2+∠3+∠4+∠5=440°,
∴∠6+∠7+∠C=720°﹣440°=280°,
∵多边形BCDG是四边形,
∴∠C+∠6+∠7+∠G=360°,
∴∠G=360°﹣(∠6+∠7+∠C)=360°﹣280°=80°,
故选:C.
4.解:设这个多边形的边数为n,
依题意得:(n﹣2)180°=360°,
解得n=9,
故选:C.
5.解:设这个多边形的边数为n,依题意得
(n﹣2)?180°=5×360°,
解得n=12,
∴这个多边形是十二边形,
故选:D.
6.解:多边形的内角和可以表示成(n﹣2)?180°(n≥3且n是整数),n应为整数,所以n﹣2也是整数,所以多边形的内角能被180整除,因为在这四个选项中不是180°的倍数的只有1200°.
故选:D.
7.解:∵∠1、∠2、∠3、∠4的外角的角度和为230°,
∴∠1+∠2+∠3+∠4+230°=4×180°,
∴∠1+∠2+∠3+∠4=490°,
∵五边形OAGFE内角和=(5﹣2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°﹣490°=50°,
故选:A.
8.解:∵从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,
∴=72°,
∴每走完一段直路后沿向右偏72°方向行走.
故选:A.
9.解:根据题意可得:a=(4﹣2)×180°,b=(5﹣2)×180°,
∴b=a+180°.
故选:D.
10.解:∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×10=80(m).
故选:B.
二.填空题(共5小题)
11.解:七边形ABCDEFG的内角和的度数为:(7﹣2)×180°=900°.
故答案为:900°.
12.解:∵多边形的内角小于120°,
∴外角大于60°,
∴这个多边形小于120°的内角的个数<360°÷60°=6,
∴在一个多边形中,小于120度的内角最多有5个.
故答案为:5.
13.过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
14.解:∵∠C=90°,
∴∠A+∠B=90°,
∵∠1+∠A+∠B+∠2=360°,
∴∠1+∠2=360°﹣90°=270°,
故答案为:270.
15.解:∵正多边形的外角和是360°,
∴360°÷9=40°.
故答案为:40.
三.解答题(共5小题)
16.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
17.解:(1)如图甲,点D是△ABC中BC边延长线上的一点,
过点C作CE∥AB,则有如下推理证明:
∵CE∥AB(已知),
∴∠ACE=∠A(两直线平行,内错角相等),∠ECD=∠B(两直线平行,同位角相等),
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B(等量代换).
(2)如图乙,根据(1)中的平行线的构造方法,
过点D作DE∥AB交BC于点E,
运用(1)中的结论,即可推理出四边形ABCD中∠A+∠B+∠C+∠CDA的度数.
由(1)知:∠BED=∠C+∠CDE.
∵DE∥AB,
∴∠A+∠ADE=180°(两直线平行,同旁内角互补),∠B+∠BED=180°(两直线平行,同旁内角互补).
∵∠CD4=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=360°(等量代换)
故答案为:(1)∠A;内错角相等;∠B;同位角相等;∠A+∠B;(2)∠CDE;∠A;同旁内角互补;360.
18.证明:∵四边形ABCD的四个角都是直角,
∴∠ABC=∠ADC=90°
(
直角定义
).
∵BE平分∠ABC,DF
平分∠ADC,
∴∠EBC=∠ABC=×90°=45°,∠ADF=∠ADC=×90°=45°,
∴∠EBC=∠ADF,
∵AD∥BC,
∴∠ADF=∠DFC(两直线平行,内错角相等).
∴∠EBC=∠DFC(等量代换),
∴BE∥DF(同位角相等,两直线平行).
故答案为:90;两直线平行,内错角相等;同位角相等,两直线平行.
19.解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
20.解:(2)延长BC交AD于点M
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(3)如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β.
由(2)可知,,
解得x=64°
故答案为64.
