人教版八年级上册 12.3 角的平分线的性质 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册 12.3 角的平分线的性质 同步练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览



文档简介
角的平分线的性质
同步练习
一.选择题(共12小题)
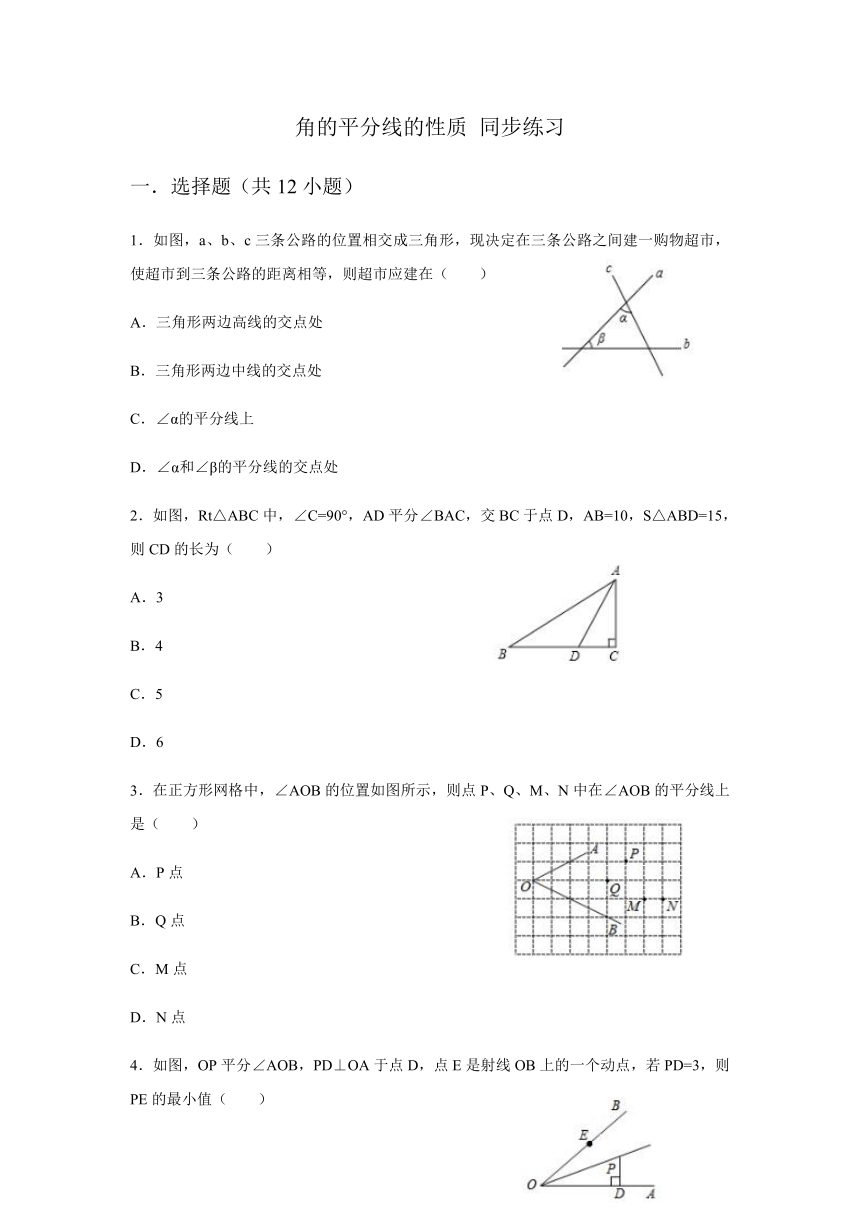
1.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( )
A.三角形两边高线的交点处
B.三角形两边中线的交点处
C.∠α的平分线上
D.∠α和∠β的平分线的交点处
2.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
3.在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N中在∠AOB的平分线上是( )
A.P点
B.Q点
C.M点
D.N点
4.如图,OP平分∠AOB,PD⊥OA于点D,点E是射线OB上的一个动点,若PD=3,则PE的最小值( )
A.等于3
B.大于3
C.小于3
D.无法确定
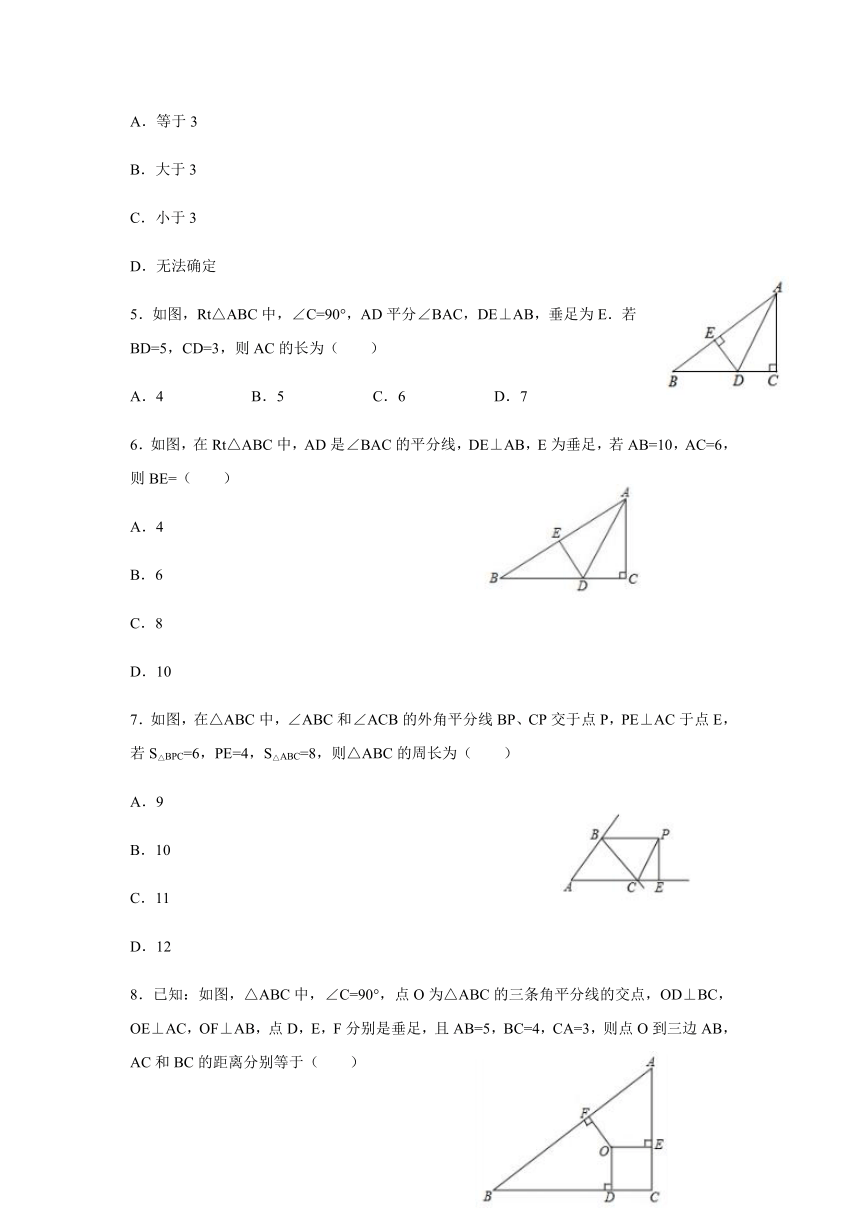
5.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BD=5,CD=3,则AC的长为( )
A.4
B.5
C.6
D.7
6.如图,在Rt△ABC中,AD是∠BAC的平分线,DE⊥AB,E为垂足,若AB=10,AC=6,则BE=( )
A.4
B.6
C.8
D.10
7.如图,在△ABC中,∠ABC和∠ACB的外角平分线BP、CP交于点P,PE⊥AC于点E,若S△BPC=6,PE=4,S△ABC=8,则△ABC的周长为( )
A.9
B.10
C.11
D.12
8.已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F分别是垂足,且AB=5,BC=4,CA=3,则点O到三边AB,AC和BC的距离分别等于( )
A.1,1,1
B.2,2,2
C.3,3,3
D.1,2,3
9.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
①∠AED=90°
②∠ADE=∠CDE
③DE=BE
④AD=AB+CD,
四个结论中成立的是( )
A.①②④
B.①②③
C.②③④
D.①③
10.如图,AD是△ABC的角平分线,DE⊥AC,DF⊥AB,E,F分别是垂足,若BD=2CD,AB=6,则AC的长为( )
A.3
B.6
C.9
D.12
11.如图,AD是∠BAC的平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=4,则AC的长是( )
A.5
B.6
C.8
D.7
12.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②∠AGH=∠BAE+∠ACB;③S△AEB:S△AEC=AB:AC,其中正确的结论有( )个.
A.0
B.1
C.2
D.3
二.填空题(共5小题)
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
14.已知:DA平分∠CAB,DB平分∠ABC,DE⊥AB于点E,△ABC的周长是12,面积是6,则DE的长是
.
15.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=5,将∠ACB平移使其顶点C与点I重合,则图中阴影部分的周长为
.
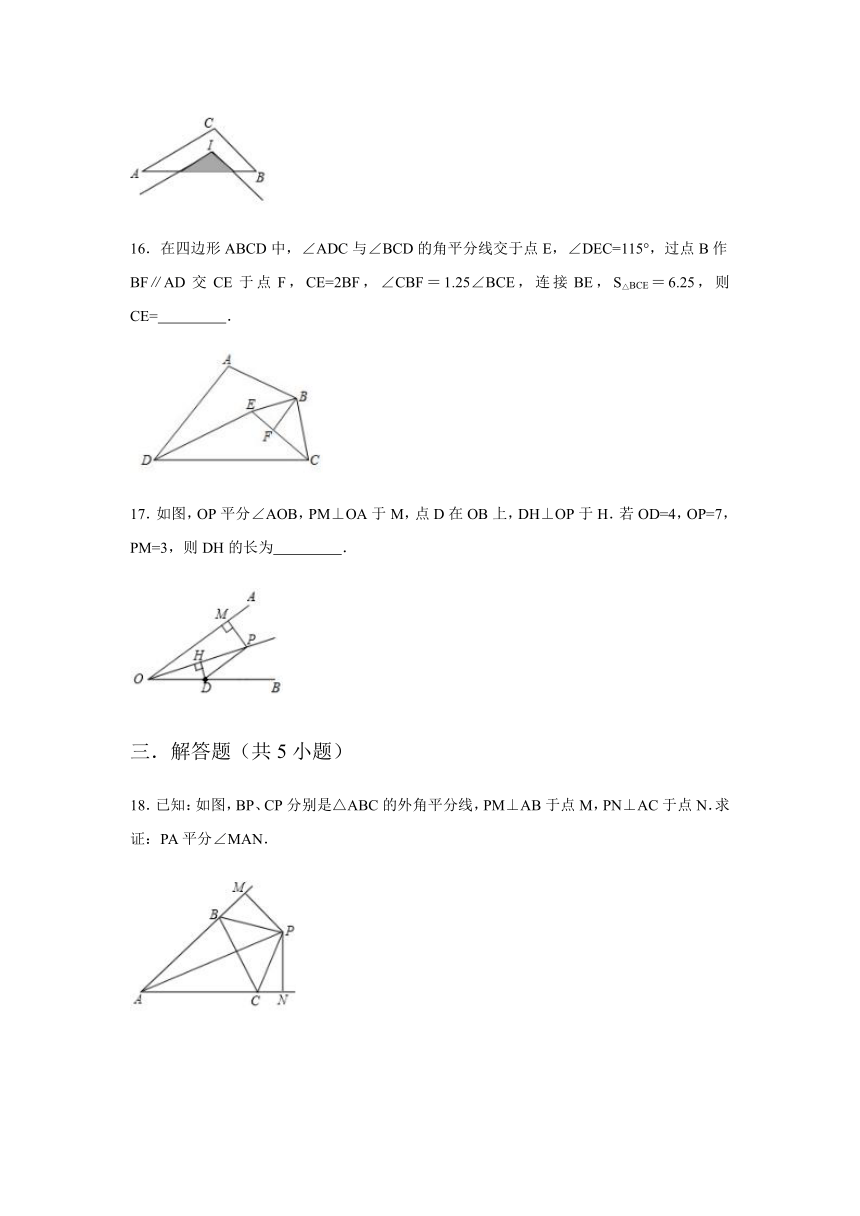
16.在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF=1.25∠BCE,连接BE,S△BCE=6.25,则CE=
.
17.如图,OP平分∠AOB,PM⊥OA于M,点D在OB上,DH⊥OP于H.若OD=4,OP=7,PM=3,则DH的长为
.
三.解答题(共5小题)
18.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
19.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F.求证:DE=BF.
20.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
21.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
22.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
参考答案
1-5:DABAC
6-10:ABAAA
11-12:AD
13、30°
14、1
15、8
16、5
18、、作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19、:∵CD平分∠ACB,
∴∠1=∠2,
∵∠1=∠2,DE⊥AC,∠ABC=90°
∴DE=BD,
∵∠3=90°-∠1,∠4=90°-∠2,
∴∠3=∠4,
∵BF∥DE,
∴∠4=∠5,
∴∠3=∠5,
∴BD=BF,
∴DE=BF.
20、连接BF,
∵F是△ABC的角平分线交点,
∴BF也是角平分线,
∵FM⊥AB,FN⊥BC,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=
1
2
∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
∴△DNF≌△EMF(AAS),
∴FE=FD.
21、(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12-x,
解得x=2,即CF=2.
22、(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴5-x=3+x,
解得:x=1,
∴BE=1,AE=AB-BE=5-1=4.
同步练习
一.选择题(共12小题)
1.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( )
A.三角形两边高线的交点处
B.三角形两边中线的交点处
C.∠α的平分线上
D.∠α和∠β的平分线的交点处
2.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
3.在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N中在∠AOB的平分线上是( )
A.P点
B.Q点
C.M点
D.N点
4.如图,OP平分∠AOB,PD⊥OA于点D,点E是射线OB上的一个动点,若PD=3,则PE的最小值( )
A.等于3
B.大于3
C.小于3
D.无法确定
5.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BD=5,CD=3,则AC的长为( )
A.4
B.5
C.6
D.7
6.如图,在Rt△ABC中,AD是∠BAC的平分线,DE⊥AB,E为垂足,若AB=10,AC=6,则BE=( )
A.4
B.6
C.8
D.10
7.如图,在△ABC中,∠ABC和∠ACB的外角平分线BP、CP交于点P,PE⊥AC于点E,若S△BPC=6,PE=4,S△ABC=8,则△ABC的周长为( )
A.9
B.10
C.11
D.12
8.已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F分别是垂足,且AB=5,BC=4,CA=3,则点O到三边AB,AC和BC的距离分别等于( )
A.1,1,1
B.2,2,2
C.3,3,3
D.1,2,3
9.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
①∠AED=90°
②∠ADE=∠CDE
③DE=BE
④AD=AB+CD,
四个结论中成立的是( )
A.①②④
B.①②③
C.②③④
D.①③
10.如图,AD是△ABC的角平分线,DE⊥AC,DF⊥AB,E,F分别是垂足,若BD=2CD,AB=6,则AC的长为( )
A.3
B.6
C.9
D.12
11.如图,AD是∠BAC的平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=4,则AC的长是( )
A.5
B.6
C.8
D.7
12.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②∠AGH=∠BAE+∠ACB;③S△AEB:S△AEC=AB:AC,其中正确的结论有( )个.
A.0
B.1
C.2
D.3
二.填空题(共5小题)
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
14.已知:DA平分∠CAB,DB平分∠ABC,DE⊥AB于点E,△ABC的周长是12,面积是6,则DE的长是
.
15.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=5,将∠ACB平移使其顶点C与点I重合,则图中阴影部分的周长为
.
16.在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF=1.25∠BCE,连接BE,S△BCE=6.25,则CE=
.
17.如图,OP平分∠AOB,PM⊥OA于M,点D在OB上,DH⊥OP于H.若OD=4,OP=7,PM=3,则DH的长为
.
三.解答题(共5小题)
18.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
19.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F.求证:DE=BF.
20.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
21.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
22.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
参考答案
1-5:DABAC
6-10:ABAAA
11-12:AD
13、30°
14、1
15、8
16、5
18、、作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19、:∵CD平分∠ACB,
∴∠1=∠2,
∵∠1=∠2,DE⊥AC,∠ABC=90°
∴DE=BD,
∵∠3=90°-∠1,∠4=90°-∠2,
∴∠3=∠4,
∵BF∥DE,
∴∠4=∠5,
∴∠3=∠5,
∴BD=BF,
∴DE=BF.
20、连接BF,
∵F是△ABC的角平分线交点,
∴BF也是角平分线,
∵FM⊥AB,FN⊥BC,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=
1
2
∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
∴△DNF≌△EMF(AAS),
∴FE=FD.
21、(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12-x,
解得x=2,即CF=2.
22、(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴5-x=3+x,
解得:x=1,
∴BE=1,AE=AB-BE=5-1=4.
