人教版数学七年级上册1.2.3相反数课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.3相反数课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 13:29:32 | ||
图片预览






文档简介
(共20张PPT)
1.2.3
相反数
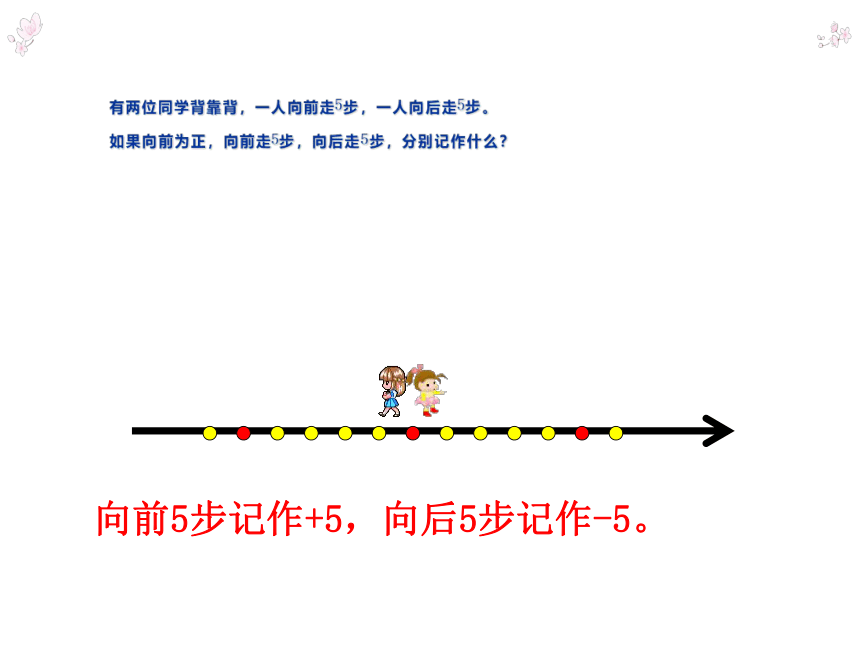
有两位同学背靠背,一人向前走5步,一人向后走5步。
如果向前为正,向前走5步,向后走5步,分别记作什么?
向前5步记作+5,向后5步记作-5。
请观察下列四组数,它们有什么共同特征?
+5
和–5
,
-
1.5
与
+1.5
共同点:
只有符号不同.
像这样只有符号不同的两个数称互为相反数
例1:
下列各数的相反数是什么?
解:
的相反数是
的相反数是
的相反数是
的相反数是
的相反数是
一般地,数a
的相反数是-a,a可以是正数,也可以是负数或0。求一个数的相反数即在它前面加一个“-”号。
-a就是表示数a的相反数。
a的相反数是
-a
a
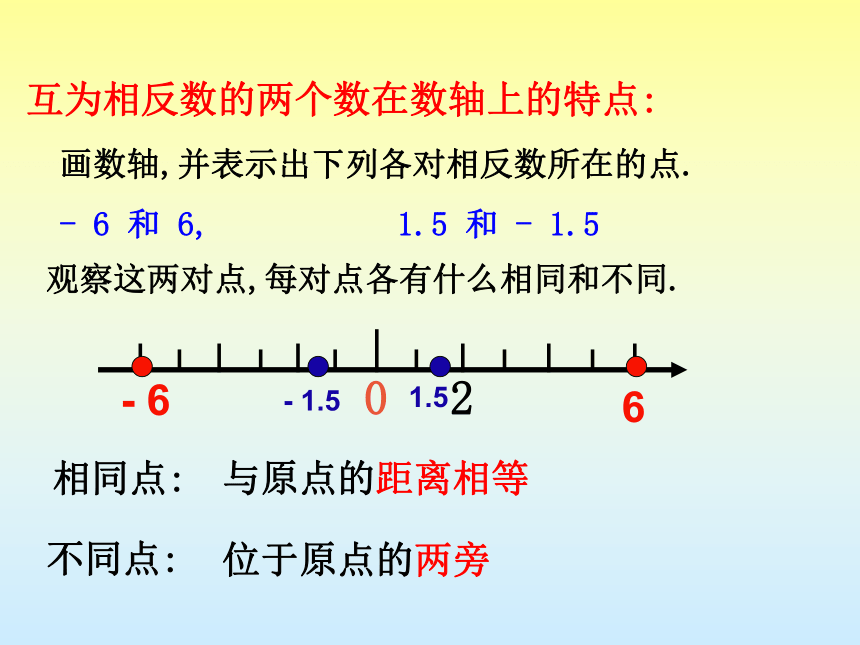
画数轴,并表示出下列各对相反数所在的点.
-
6
和
6,
1.5
和
-
1.5
观察这两对点,每对点各有什么相同和不同.
0
2
-
6
6
-
1.5
1.5
相同点:
不同点:
互为相反数的两个数在数轴上的特点:
与原点的距离相等
位于原点的两旁
0
2
-
6
6
-
1.5
1.5
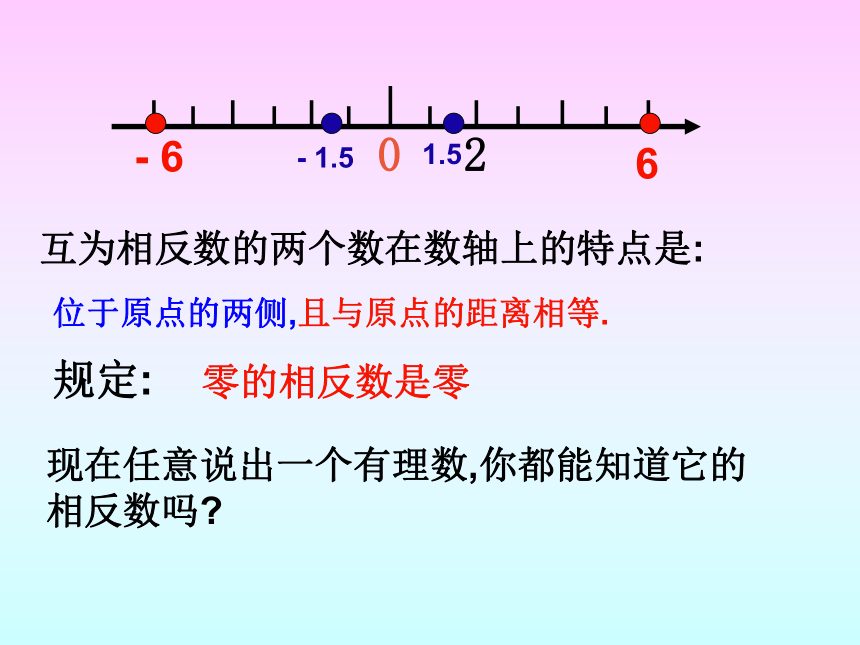
互为相反数的两个数在数轴上的特点是:
位于原点的两侧,且与原点的距离相等.
规定:
零的相反数是零
现在任意说出一个有理数,你都能知道它的相反数吗?
如(1)当a=7
-a=-7
表示数7的相反数是-7
(2)当a=0
-a=-0=0
表示0的相反数是0
(3)当a=-6
-a
=-(-6)=6
表示-6的相反数是6
练习:说出下列各式的意义
(1)-(-7.5)的意义是_______________
(2)-(+9)的意义是__________________
(3)-(-0.5)的意义是________________
表示-7.5的相反数
表示+9的相反数
表示-0.5的相反数
例2、说出下列各式的意义并化简符号
(1)、-(+3)
(2)、-(-4)
解
(1)
-(+3)表示+3的相反数
所以
-(+3)=-3
(2)-(-4)表示-4的相反数
所以-(-4)=4
结论:要化简符号,首先要弄清意义。
1.
在一个数的前面加上一个“
–
”号,表示原来那个数的相反数。
例如:-
4
,
+
5.5
的相反数分别是:
-
(
-
4
)
-
(
+
5.5
)
=
4
=
-
5.5
2.
在一个数的前面添上“+”号,即表示这个数本身.
例如:
+
(
-
4
)
+
(
+
5.5
)
=
-
4
=
5.5
练习1.
化简下列各数:
–
(
+
10
)
(2)
+
(–20.15
)
(3)
+
(
+
3
)
(4)
–
(–20
)
解:
(1)
原式
=
-
10
(2)
原式
=
-
20.15
(3)
原式
=
3
(4)
原式
=
20
课堂基础练习1
1、正数的相反数一定是_______数;
2、负数的相反数一定是_______数;
3、_____的相反数是它本身.
负
正
0
基础练习2:判断题
1、符号不同的两数叫做相反数(
)
2、一个数的相反数一定是负数。(
)
3、-6是相反数。(
)
4、0的相反数是它本身。(
)
1、2a的相反数是___________
2、
的相反数是____________
3、(1)-(+2.6)的意义是__________
化简符号后为______________
(2)-(-7)的意义___________
化简符号后为______________
4、一个数m的相反数是-5,则3m-2=____
5、若a=-7,则-a=____,若-x=-7,则2x=____
-2a
表示+2.6的相反数
-2.6
表示-7的相反数
7
13
7
14
拓宽练习
a的相反数-a前有负号,那么-a一定是负数吗?
辩
一
辩
6、2的相反数的相反数是___________.
7、若a和b是互为相反数,那么a+b=_______.
2
0
应用创新
如图:是一个正方形纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次为_____
______
_____
A
B
-1
2
C
0
0
1
-2
若2前面有2000个正号,化简后的结果是 .
若2前面有2001个负号,化简后的结果是 .
讨论
-4
+6
8
-7
2
-2
归纳
符号化简规律:一个数符号的改变与前面的正号无关,与负号个数有关.当负号的个数为奇数时,这个数的符号改变,当负号的个数为偶数时,这个数的符号不变.
奇负偶正
知识小结
(3)、数轴上表示相反数的两个对应点,分别位于原点
两侧,它们到原点距离相等。
(1)、只有符号不同的两个数才互为相反数。
(2)、相反数成对出现。
(4)、符号的化简
再
见!
1.2.3
相反数
有两位同学背靠背,一人向前走5步,一人向后走5步。
如果向前为正,向前走5步,向后走5步,分别记作什么?
向前5步记作+5,向后5步记作-5。
请观察下列四组数,它们有什么共同特征?
+5
和–5
,
-
1.5
与
+1.5
共同点:
只有符号不同.
像这样只有符号不同的两个数称互为相反数
例1:
下列各数的相反数是什么?
解:
的相反数是
的相反数是
的相反数是
的相反数是
的相反数是
一般地,数a
的相反数是-a,a可以是正数,也可以是负数或0。求一个数的相反数即在它前面加一个“-”号。
-a就是表示数a的相反数。
a的相反数是
-a
a
画数轴,并表示出下列各对相反数所在的点.
-
6
和
6,
1.5
和
-
1.5
观察这两对点,每对点各有什么相同和不同.
0
2
-
6
6
-
1.5
1.5
相同点:
不同点:
互为相反数的两个数在数轴上的特点:
与原点的距离相等
位于原点的两旁
0
2
-
6
6
-
1.5
1.5
互为相反数的两个数在数轴上的特点是:
位于原点的两侧,且与原点的距离相等.
规定:
零的相反数是零
现在任意说出一个有理数,你都能知道它的相反数吗?
如(1)当a=7
-a=-7
表示数7的相反数是-7
(2)当a=0
-a=-0=0
表示0的相反数是0
(3)当a=-6
-a
=-(-6)=6
表示-6的相反数是6
练习:说出下列各式的意义
(1)-(-7.5)的意义是_______________
(2)-(+9)的意义是__________________
(3)-(-0.5)的意义是________________
表示-7.5的相反数
表示+9的相反数
表示-0.5的相反数
例2、说出下列各式的意义并化简符号
(1)、-(+3)
(2)、-(-4)
解
(1)
-(+3)表示+3的相反数
所以
-(+3)=-3
(2)-(-4)表示-4的相反数
所以-(-4)=4
结论:要化简符号,首先要弄清意义。
1.
在一个数的前面加上一个“
–
”号,表示原来那个数的相反数。
例如:-
4
,
+
5.5
的相反数分别是:
-
(
-
4
)
-
(
+
5.5
)
=
4
=
-
5.5
2.
在一个数的前面添上“+”号,即表示这个数本身.
例如:
+
(
-
4
)
+
(
+
5.5
)
=
-
4
=
5.5
练习1.
化简下列各数:
–
(
+
10
)
(2)
+
(–20.15
)
(3)
+
(
+
3
)
(4)
–
(–20
)
解:
(1)
原式
=
-
10
(2)
原式
=
-
20.15
(3)
原式
=
3
(4)
原式
=
20
课堂基础练习1
1、正数的相反数一定是_______数;
2、负数的相反数一定是_______数;
3、_____的相反数是它本身.
负
正
0
基础练习2:判断题
1、符号不同的两数叫做相反数(
)
2、一个数的相反数一定是负数。(
)
3、-6是相反数。(
)
4、0的相反数是它本身。(
)
1、2a的相反数是___________
2、
的相反数是____________
3、(1)-(+2.6)的意义是__________
化简符号后为______________
(2)-(-7)的意义___________
化简符号后为______________
4、一个数m的相反数是-5,则3m-2=____
5、若a=-7,则-a=____,若-x=-7,则2x=____
-2a
表示+2.6的相反数
-2.6
表示-7的相反数
7
13
7
14
拓宽练习
a的相反数-a前有负号,那么-a一定是负数吗?
辩
一
辩
6、2的相反数的相反数是___________.
7、若a和b是互为相反数,那么a+b=_______.
2
0
应用创新
如图:是一个正方形纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次为_____
______
_____
A
B
-1
2
C
0
0
1
-2
若2前面有2000个正号,化简后的结果是 .
若2前面有2001个负号,化简后的结果是 .
讨论
-4
+6
8
-7
2
-2
归纳
符号化简规律:一个数符号的改变与前面的正号无关,与负号个数有关.当负号的个数为奇数时,这个数的符号改变,当负号的个数为偶数时,这个数的符号不变.
奇负偶正
知识小结
(3)、数轴上表示相反数的两个对应点,分别位于原点
两侧,它们到原点距离相等。
(1)、只有符号不同的两个数才互为相反数。
(2)、相反数成对出现。
(4)、符号的化简
再
见!
